网站建设有云端吗做百度收录的网站

文|琥珀食酒社
作者 | 积溪
一只猴子能值多少钱?
答案是:13个小目标
这两天
只要你家没有断网
一定会被这只猴子刷屏
它就是咱国产的3A游戏
《黑神话:悟空》
这只猴子到底有多火?
这么跟你说吧
茅台见了它都得叫声:猴哥
和它联名的某咖啡品牌
8W杯咖啡上线就被秒空
核销的服务器都快干趴了
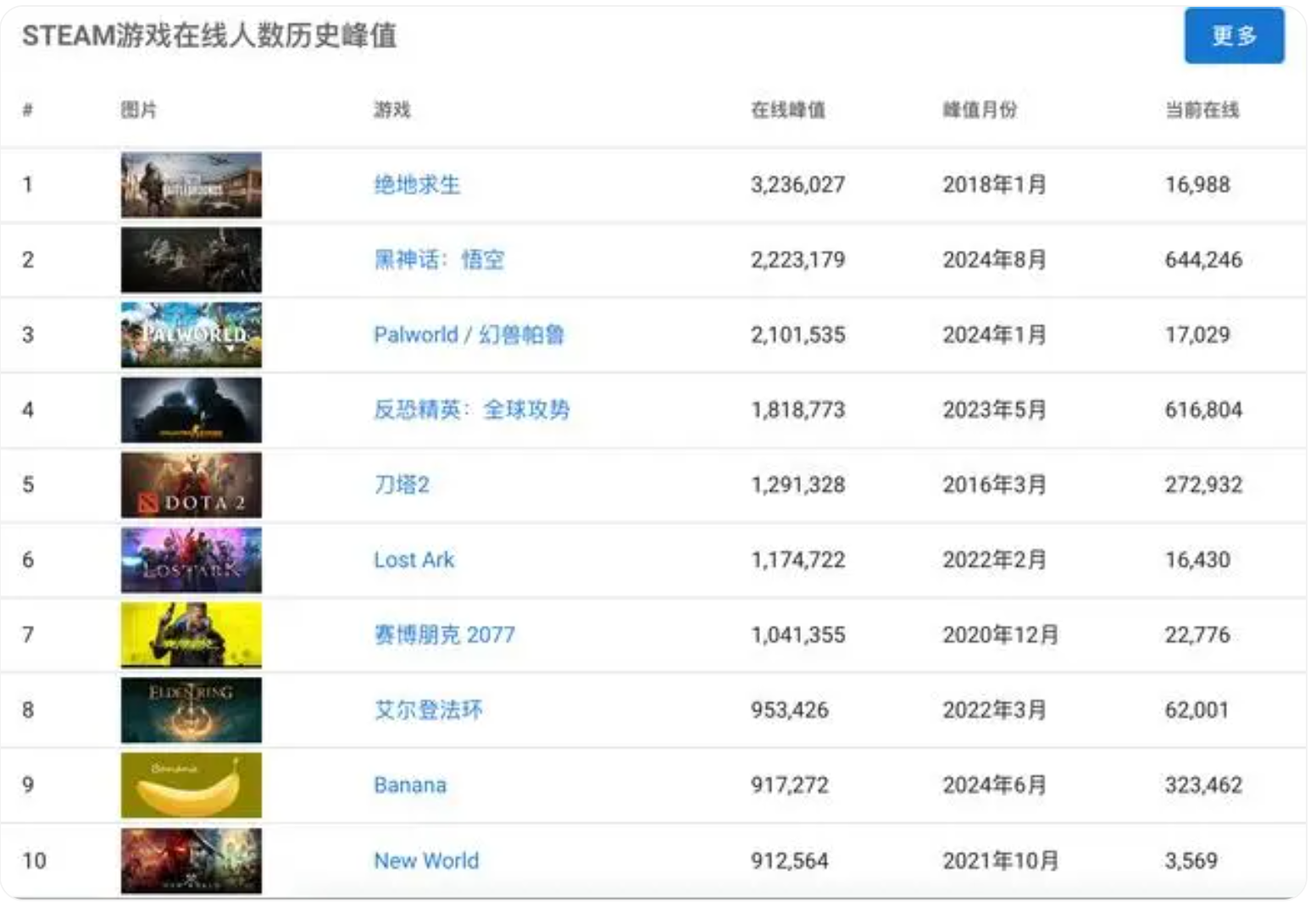
上线第一天
最高在线人数222万
力压《幻兽帕鲁》
仅次于《绝地求生》
霸榜了各大平台的热门
全世界的玩家都在等待
解压进度条
有的人解压时间竟然要500年
这还是周二,是工作日噢
有这么多人不用上班的吗?
如果周末上线
不知道要火爆成啥样
我不是游戏博主
但我今天想从财经的角度
来聊聊这款游戏
在我看来
这不只是游戏产业的突破
还有更重要的意义
从商业的角度来看
这只猴子已经创造了历史
从开启预售到正式上线
一个月的销量已经接近4亿元
而根据业内从士的预测
这款游戏的全平台销量
有望达500-700万套
消售额大概在13.4亿
到18.76亿之间
没有任何一款单机游戏
能拥有如此现象级的影响力
但它取得的成就
远远不止这些
作为第一款3A大作
这是咱们的游戏产业
站起来的标志
一直以来3A游戏
就是高成本、高体量、高质量的代名词
但提到咱们的游戏产业
你脑袋里最先冒出来的是啥?
是不是低质量、圈钱、电子赌博?
虽然很扎心,但这就是现实
什么文化输出、属于咱们自己的IP
那就更遥远了了
反而是别人
拿着咱们的IP大赚特赚
玩过《三国》的人应该都知道
《三国志》和《三国无双》
是日本游戏厂商推出的
《全面战争:三国》
是欧美厂商做出来的
总之就是和咱没有关系
还有咱们的国宝熊猫
在全球传播最广的《功夫熊猫》
是美国梦工厂出品的

在《黑神话:悟空》走红之前
火爆全球的也不是咱们的《西游记》
而是日本的动画《龙珠》
咱自己的IP
却成了别人的摇钱树
你知道一个顶级IP有多赚钱吗?
宝可梦单是版权收入
一年就有136.48亿元

一个顶级IP
不仅能带动游戏和影视产业的发展
出版、文旅、还有IP衍生品等
最关键的是
这些IP带来的不只是商业价值
还有文化输出
不少外国网友们为了玩这个游戏
猛啃《西游戏记》的原著
不只是这只猴子
还有独属于咱们的极致美学
中国的建筑
这《黑神话:悟空》的取景地
山西省就有27个
占比超过一半,
山西文物这下可就藏不住了
而这就是游戏IP最大的价值
你觉得呢?
*本文图片均来源于网络
扎根新消费,探索新商业,研究消费者、观察产业链。
