做网站来钱快手机ppt制作软件
在现代制造业中,提高设备综合效率(Overall Equipment Efficiency,OEE)是企业追求高效生产和优化生产能力的重要目标之一。OEE是一个关键的绩效指标,可以帮助企业评估设备的利用效率、生产效率和质量水平。本文将从三个方面探讨如何改善设备综合效率并提高工厂的生产力。
OEE的定义及计算方法
OEE是一个用于衡量设备综合效率的指标。它提供了一个评估设备在生产过程中的效率和性能的方法,将设备的利用率、生产效率和质量水平综合考虑在内。它通常通过以下公式计算:
OEE = 设备可用率 × 性能效率 × 质量合格率
其中:
1. 设备可用率(Availability)衡量设备在计划生产时间内的可用性,包括停机时间、故障修复时间和计划维护时间。
设备利用率 = (计划生产时间 - 停机时间)/ 计划生产时间
2. 性能效率(Performance)衡量实际生产速度与理论生产速度之间的差异,包括设备速度损失和小停机损失。
性能效率 = 实际生产数量 / (理论生产速度 × 计划生产时间)
3. 质量合格率(Quality)衡量产品的合格数量与总产量之间的比例,包括次品品质和停机品质。
质量合格率 = 合格产品数量 / 总产量
更多OEE的相关介绍可查看往期文章>>什么是OEE?它的作用是什么?
提高OEE的意义
改善设备综合效率和提高OEE对企业具有重要意义。
1. 提高生产效率:通过优化设备利用率和生产效率,企业能够提高生产效率,减少生产时间和资源浪费,从而提高生产能力和产出。

图.提高设备生产效率(全景网)
2. 降低生产成本:通过减少停机时间、优化设备速度和提高质量合格率,企业可以降低生产成本,提高生产效益。
3. 提升产品质量:通过关注质量合格率并采取相应的改进措施,企业可以提升产品质量,满足客户需求,增强市场竞争力。
4. 实现持续改进:OEE作为一个综合指标,可以帮助企业全面了解生产过程中的瓶颈和问题点,并提供改进的方向。通过持续监控和改进OEE,企业可以实现持续改进和持续增长。
如何通过设备健康管理平台PreMaint提高OEE
现代的设备健康管理系统如PreMaint能够帮助企业实现OEE的持续改善和生产力的提高。
1. 实时数据监测与分析:PreMaint平台可以实时收集和监测设备数据,包括设备状态、运行参数和故障信息等。通过对这些数据进行分析,企业可以及时发现潜在问题,并采取预防性维护措施,减少停机时间和故障率,提高设备利用率。
2. 故障预测与预警:PreMaint平台基于先进的算法和机器学习技术,可以对设备进行故障预测和预警。通过提前预测设备故障,并及时采取维护措施,企业可以避免意外停机和生产中断,提高设备利用率和生产效率。
3. 维护计划和任务管理:PreMaint平台可以帮助企业建立维护计划和任务管理,确保设备的定期维护和保养。通过合理的维护计划和任务安排,企业可以减少计划维护时间,最大限度地提高设备的可用性和生产时间。
4. 数据可视化与报告分析:PreMaint平台提供直观的数据可视化界面和详细的报告分析功能,帮助企业全面了解设备的运行状况和维护情况。通过对数据和报告的分析,企业可以发现设备性能改进的机会,并制定相应的优化策略,提高生产效率和质量水平。
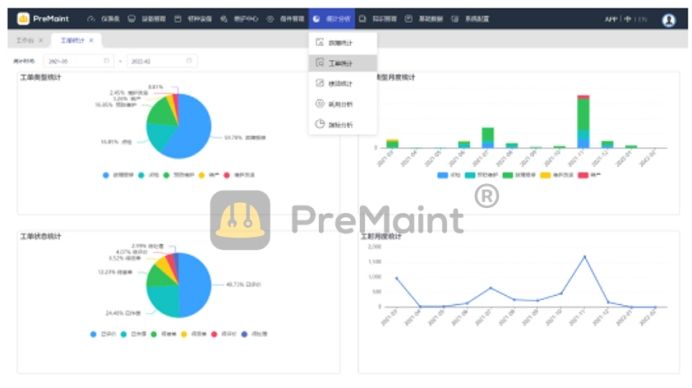
图.可视化报表分析(PreMaint)
改善设备综合效率OEE对于提高工厂的生产力至关重要。通过定义和计算OEE指标,并关注设备利用率、生产效率和质量合格率三个方面,企业可以全面评估和改进设备的综合效率。此外,借助设备健康管理平台PreMaint的实时监测、故障预测、维护计划管理和数据分析功能,企业能够更好地管理设备,提高OEE并实现生产力的提升。通过持续改进和优化,企业将能够在竞争激烈的市场中保持竞争优势并实现可持续发展。
-关注我,不错过工业互联网&设备管理领域的最新资讯、深度干货!
-如果对本文有任何疑问,或想了解更多内容,欢迎评论留言/发送私信告诉我~
