毕设做微课资源网站设计可以吗一款教育培训咨询有限公司网站源码
探索智能体Agent的未来之路:Function Call与ReACT框架的较量,谁能引领未来?
引言
各大平台出现智能体应用创建,智能体逐渐落地,背后的使用哪种框架?
随着各大平台,例如百度千帆APPbuilder、阿里百炼、字节的扣子等等,逐渐落地智能体应用,其背后的技术和框架引起了广泛关注。智能体(Agent),也称为代理 ,是一种使用大语言模型(LLM)来促进推理过程并根据模型的建议采取行动的实体。尽管大语言模型在自然语言理解和生成方面取得了巨大进步,但仍然也存在一些限制:知识有限并难以实时更新、缺乏审查与安全控制、以及无法直接执行语言之外的任务。光使用模型本身现阶段还难以直接满足实际场景的需求,因此,开发智能体成为了一种应用解决方案。
智能体的基本概念是在没有人工定义工作流(Workflow)的情况下,利用外部工具或功能,选择要执行的一系列操作。对于 toB 产品,智能体能够解决功能点繁多、使用链路冗长、使用方法复杂难上手等问题。从技术角度来看,智能体通过大模型理解用户意图并生成结构化描述,进而执行相关操作。因此,智能体在实际应用中扮演着至关重要的角色,成为了连接大模型和现有应用的桥梁。
市场上现在出现了众多种类的智能体应用,其中大致可以分为两种主要的方式:以ReACT行动链为主的较为复杂的智能体结构,和以Function Calling(函数调用)模型为主的轻量级智能体结构。
一、 两种框架原理概述:
“吟游诗人分为两种,一种懂得如何写诗,另一种懂得根据意境引用别人写的诗”
1.1. ReACT 大致原理与历史
在大模型的涌现能力刚被人们发掘的时候,人们意识到生成式AI的潜力可能不止局限于文本内容的生成,如果让大模型能够和外部世界交互,是不是就能获得更广泛的信息,甚至对外部环境造成一定影响?基于这个出发点,研究者把推理(例如思维链提示)和行动(例如 WebGPT、SayCan、ACT-1)进行结合,并提出了ReACT框架,其核心思想是将推理和行动结合起来,形成一个智能、自主的智能体结构,并拥有与外部环境交互的能力。
ReACT框架的一个关键特点是其任务拆解模块,能够将复杂的任务拆解成一系列更小、更明确的子任务,这些子任务更容易被模型理解和执行,让模型不再“消化不良”。例如,ReACT可以帮助模型决定进行API调用、执行查询等操作,天气预报、计算器是大家耳熟能详的例子。这样,模型就可以在与外部源交互的过程中收集更多的信息,以更好地完成复杂的任务。
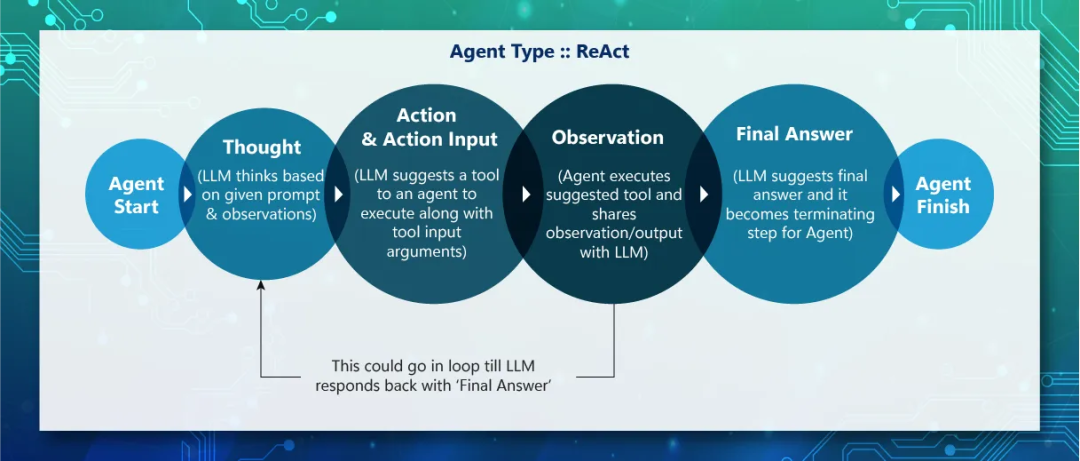
ReACT技术的一个关键挑战是如何在API调用中处理函数参数。为了解决这个问题,通常需要要求模型返回特定格式的响应,以便区分不同的阶段(思考、行动、观察)。
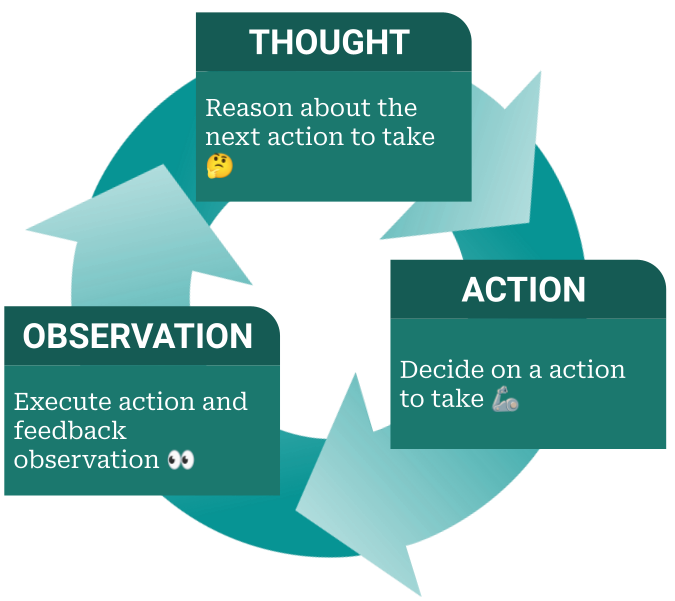
ReAct框架的应用已经在多种语言和决策任务中得到了验证,其有效性在问答、事实验证等任务中得到了展示。在早期的智能体应用尝试中,LangChain就提供了以ReACT为框架的智能体应用开发方式。基于ReAct通过与简单的维基百科API交互,生成类似人类的任务解决轨迹,比没有推理痕迹的基线更容易解释。这种方式也成为了业界对于智能体应用的早期定义:有着较为明确的自然语言规划列表,以及一套复杂的工具使用方式。
ReAct框架的成功激发了更多类似的研究和项目,如XAgent、Autogen等。这些项目都对智能体框架进行了改进和扩展,例如引入内外双循环机制、群体智能、反思Reflection等机制。这些变种的特点大多是为ReACT类的智能体结构提供更加稳定的规划以及工具的调用,但通常也会增加上下文的长度,造成模型推理费用以及时间消耗的提升。
【一一AGI大模型学习 所有资源获取处一一】
①人工智能/大模型学习路线
②AI产品经理入门指南
③大模型方向必读书籍PDF版
④超详细海量大模型实战项目
⑤LLM大模型系统学习教程
⑥640套-AI大模型报告合集
⑦从0-1入门大模型教程视频
⑧AGI大模型技术公开课名额
1.2. Function Call 大致原理与历史
OpenAI于23年6月份的更新的gpt-4-0613 and gpt-3.5-turbo-0613版本中为模型添加了Function Calling功能,通过给模型提供一组预定义的函数(Function list)以及用户提问(Query),让大模型自主选择要调用的函数,并向该函数提供所需的输入参数。随后我们就可以在自己的环境中基于模型生成的参数调用该函数,并将结果返回给大模型。

Function Calling的步骤
ChatGPT的Function Calling功能在发布之后立刻引起了人们的关注,因其简单易用的特性以及规范的输入输出迅速成为模型生态中Function calling的格式规范。后续的具有function calling功能的模型有很多参照了OpenAI的Function Calling格式,其输入的函数列表以及输出的Function Calling及其参数都以JSON格式输出:输入的函数列表中通常包括函数名称、函数功能描述、函数参数等部分,而输出中则按顺序输出所调用的函数名称和其中使用的参数
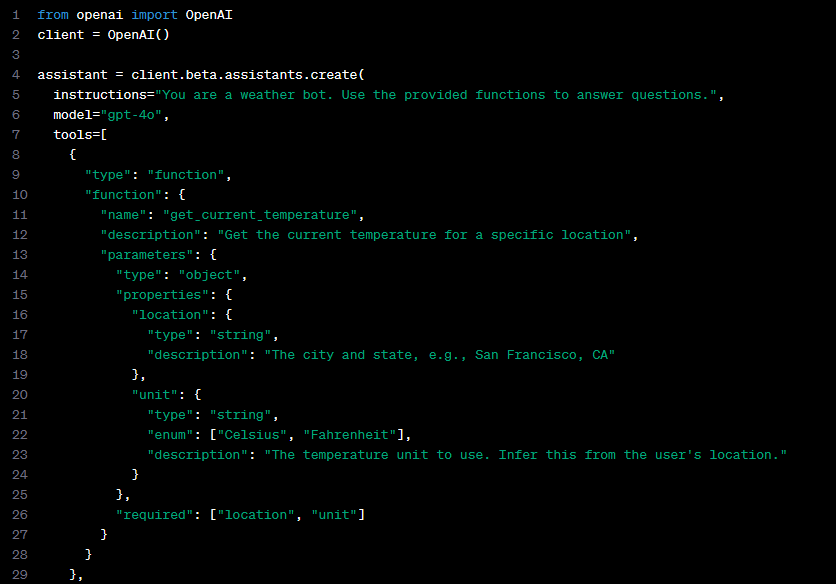
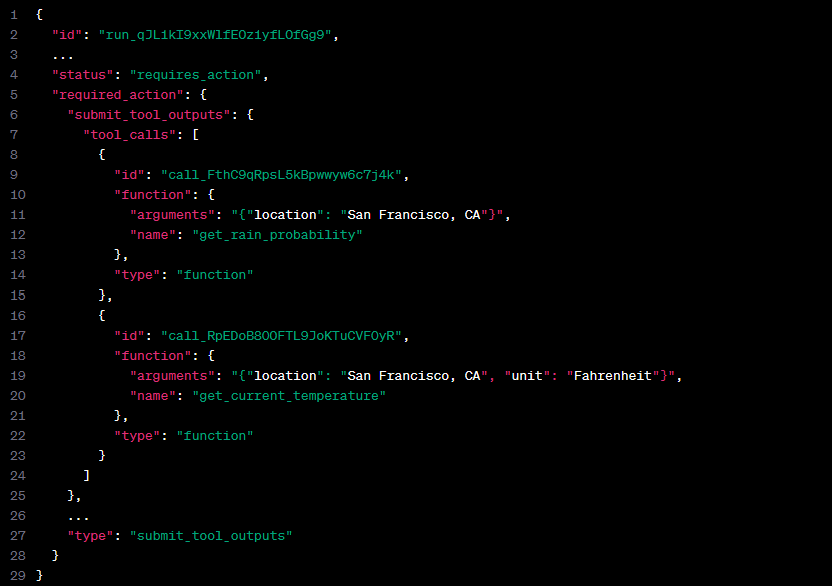
OpenAI官网输入的函数列表以及输出的Function Calling列表样例
然而Function Calling这种类型的智能体结构对模型有较高的要求,LLM模型必须进行针对性微调,以便根据用户提示检测何时需要调用函数,并使用符合函数签名的JSON进行响应;OpenAI并未开源其Function Calling相关的训练框架以及训练集,但大致推测其训练集中也包含了大量相似的工具调用JSON数据。
在开源社区中,也出现了众多开源的Function Calling模型、训练框架以及数据集。加州伯克利和微软的研究人员就开源了Gorilla模型以及Open Function系列,是一个完全针对Function Calling的LLaMA微调模型,本身在发布之时就有调用1,600+个API,准确使用工具的能力,在API使用方面超过了当时的GPT-4。事实上,Gorilla的相关论文和Github在23年5月份公布,比OpenAI GPT在6月份的更新还要更早一些。其训练集的主要成分是一种由自指令生成的{指令,API}对组成的用户-代理式的多轮聊天对话数据。

Gorilla 的工作流程
在今年二月,Gorilla开放了OpenFunction v2版本,其Function Call功能能够支持更复杂的情况,包括多函数选择,多次调用,函数相关性检测与REST格式的API调用,让其能够更有效地调用工具,并提升准确率。

OpenFunction v2的多函数选择,多次调用,函数相关性检测与REST格式的API调用
伯克利大学也在今年公布了伯克利Function Calling模型排行榜,多维度地评估 LLM 准确调用函数的能力,目前仍然处于快速更新的状态。
地址:
https://gorilla.cs.berkeley.edu/leaderboard.html
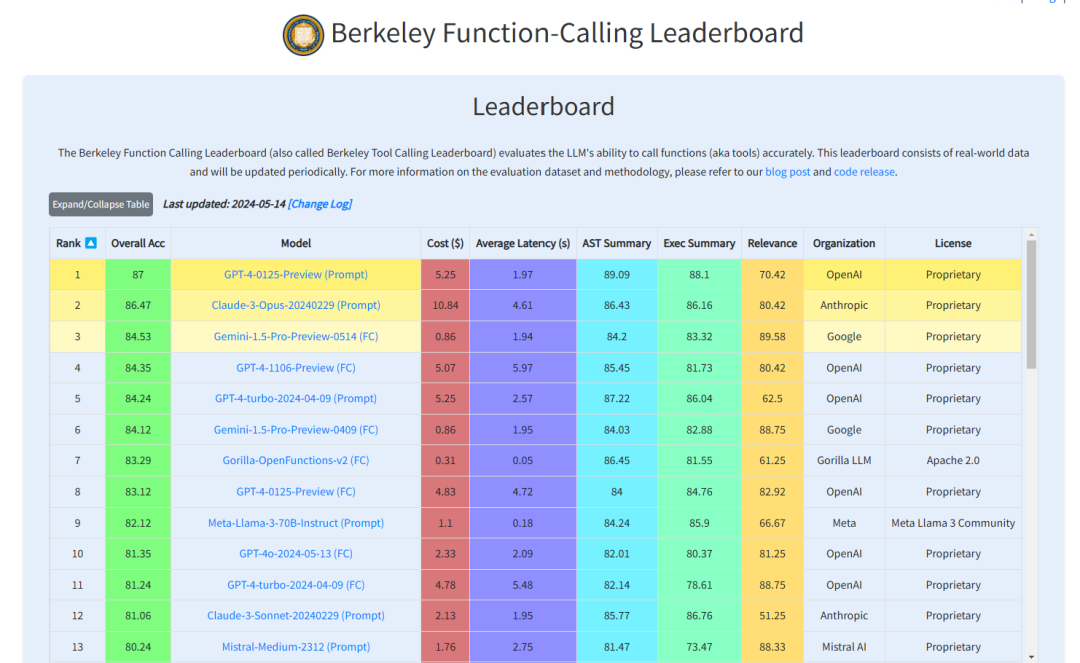
现在,许多新训练的模型当中都包含了部分Function Calling的数据集,让基础模型本身带有一定的Function Calling功能,能够适用于更加复杂的场景,其中国内的模型包括了阿里的Qwen、智谱的ChatGLM、字节的豆包等等
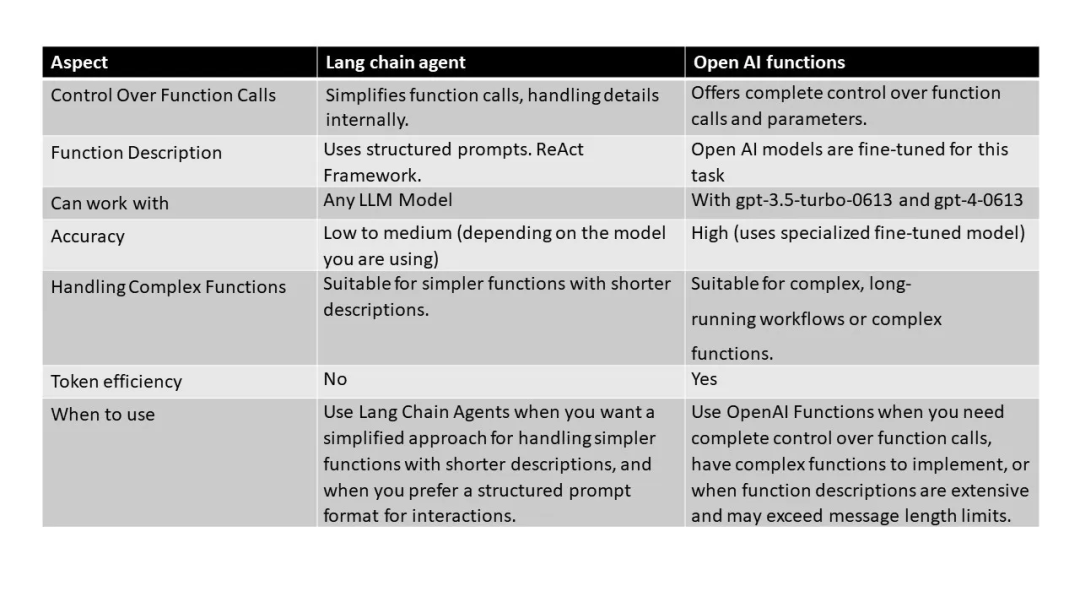
1.3. 两种框架对比的优劣势
在实际应用的时候,ReACT框架和Function Calling模型框架有不同优略势,需要从不同的角度来思考:
1.3.1. 对模型的要求
ReACT和Function Calling在对模型的要求上存在显著差异。
Function Calling类的智能体对模型的要求相对较高。模型的训练数据必须包含function call相关的内容,以确保模型能够理解和生成结构化的输出。这类模型通常还需要具备更好的结构化输出稳定性,以及关键词和信息提取的能力。这意味着,模型需要较大的参数量,经过精细的调整和优化,才能满足Function Calling的需求。这种方式的优点在于,模型可以直接生成符合特定格式的数据,从而提高了解析和处理的效率。
相比之下,ReACT框架对模型的要求则相对较低。ReACT不需要模型本身支持function calling格式的输出。在计划的生成过程中,它可以支持自然语言的规划文本,并在后续步骤中解析这些自然语言的输入。其优势在于,模型不需要进行复杂的结构化输出,只需生成自然语言即可。这使得模型的训练和优化过程更为简单,同时也降低了模型的出错率。
1.3.2. 对提示词的要求
Function Calling类的智能体结构通过微调模型来支持用户输入选择函数和结构化输入,这个过程其实这提高了输出稳定性,并简化了提示工程的复杂程度。相比之下,ReACT方式需要对模型进行更加细致的指导,让通用模型拥有输出规划、函数所需参数的能力,虽然这缓解了对模型本身输出能力的依赖,却增加了对提示工程的依赖,需要针对模型的特性来设计对应的提示模板,生成规划(函数的选择)和函数所需的API,并可能需要提供样例,消耗的上下文Token也相对更多一些。
尽管Function Calling对模型的要求更高,但通过提示模板,普通的模型也可以具备简单的Function Calling的能力。通过在prompt中说明希望的输出格式和字段描述,大模型可以直接输出符合要求的内容。
1.3.3. 对推理的要求
在智能体结构的设计中,ReACT和Function Calling在推理要求上存在显著差异。Function Calling强调的是单/多步骤的JSON输出,而ReACT则允许LLM输出一个自然语言规划,这为智能体提供了思考的空间并能在后续的执行过程中动态地修正规划(Reflection)。
Function Calling通过微调的模型,使其更擅长返回结构化输出。这种方法可以产生确定性的结果,同时降低错误率。然而,由于缺乏思维链,整个Function Calling的过程重度依赖于模型自身的推理性能,引发了大模型推理的重要问题 – 缺乏解释性,整个推理过程相较于ReACT方式更加黑盒。相比之下,ReACT的CoT部分允许智能体在执行任务时进行更深入的推理和思考。这种方法使得智能体能够更准确地理解任务,并在执行过程中进行调整。
在实际应用中,Function Calling和ReACT都可能需要执行多轮的拆解、推理和调用才能得到结果。Function Calling隐藏了Thought过程,而ReACT则更加开放和透明。这使得ReACT更适合需要高度定制和灵活性的应用场景,而Function Calling则更适合需要快速和确定性输出的场景。
1.3.4. 优略势的总结
总的来说,在智能体结构的设计中,Function Calling方式通过微调模型来支持用户输入选择函数和结构化输入,这提高了输出稳定性,简化了提示工程,无需提供示例来教导模型如何推理和输出结构化数据,其效果也更加稳定。然而,Function Calling模型方法较为黑盒,开发者可控性较低,且对大语言模型要求较高。
相比之下,ReACT方法更加通用,留给开发者的改造空间更多。ReACT支持结构化的Function Calling,但其提示的设计更为复杂,可能占用更多的上下文Token空间。ReACT方法中的模型仅依赖于通过提示模板进行的上下文学习,让生成更加灵活的同时也增加了提示模板设计的复杂程度。相较而言,在不微调模型的情况下,ReACT框架更易于拓展,基于场景设计出不同的规划结构和工具调用结构。
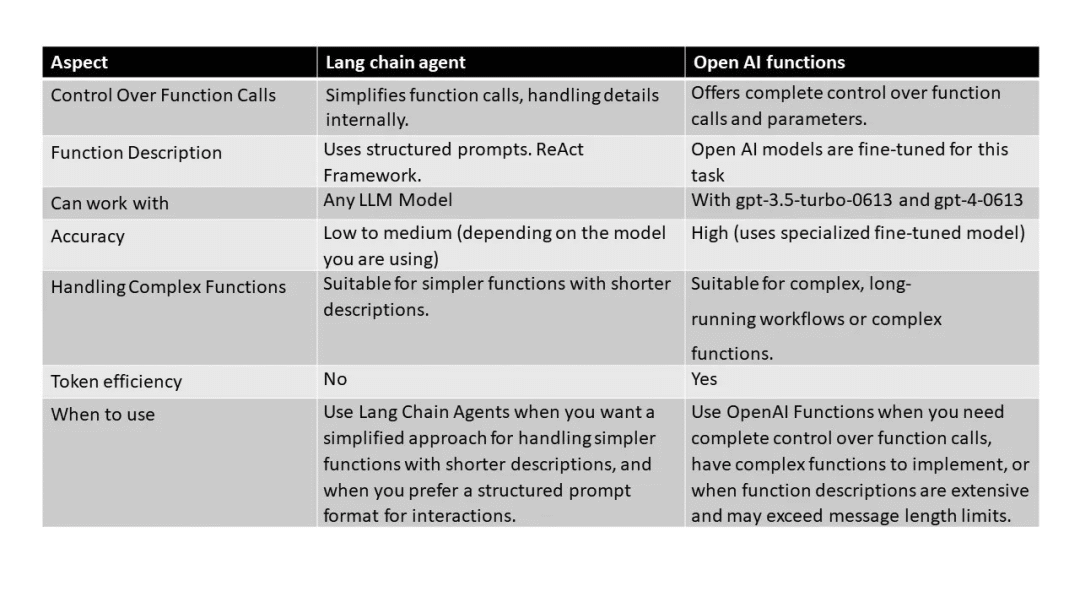
Function Calling和ReACT各有优势。Function Calling在简化流程和提高输出稳定性方面具有优势,而ReACT在通用性和灵活性方面更胜一筹。因此,在选择智能体结构时,应根据具体的应用场景和需求来决定使用哪种方法。
二. 两种框架的现状:
2.1. 国内大模型对Function Call功能的支持
阿里Qwen-Chat系列:
Qwen-Chat模型在Function Calling方面针对工具使用和Function Calling功能进行了深度优化,并在开源中文的工具调用测试集中表现出色。这使得用户能够轻松基于Qwen开发智能体类应用,甚至可以利用Python代码解释器来增强Qwen。为实现工具调用,Qwen团队依据ReAct Prompting原理提供了相关文档,并在openai_api.py中支持了Function Calling。为扩展上下文长度并打破训练序列长度的限制,Qwen的模型中引入了多种技术,如NTK感知插值、窗口注意力和LogN注意力缩放。这些技术将Qwen-14B的上下文长度从2K扩展到超过8K个标记,Qwen-1.8B/7B则从8K到32K代币,显著提升了模型在处理长文本时的性能。
智谱ChatGLM系列:
ChatGLM3-6B支持工具调用、代码执行、智能体任务等功能。对于比较复杂的问题,模型可能需要进行多次工具调用。这时,可以根据返回的response是str还是dict来区分生成的回复和工具调用请求。这些特点使得ChatGLM3-6B在处理复杂问题、执行代码和调用工具方面具有更高的灵活性和效率
月之暗面Kimi模型:
Kimi模型在Function Calling方面展现了其智能化的特点。通过在Messages中描述工具或函数,Kimi大模型能够智能地选择并输出一个包含调用一个或多个函数所需的参数的JSON对象,从而实现链接使用外部工具的目的。此外,Kimi大模型还支持使用一些智能体平台,如Coze、Bisheng、Dify和LangChain等框架,来创建和管理这些工具。这使得用户能够配合Kimi大模型设计更加复杂的工作流程。这些特点使得Kimi模型在Function Calling方面具有较高的灵活性和扩展性,能够满足用户在不同场景下的需求。
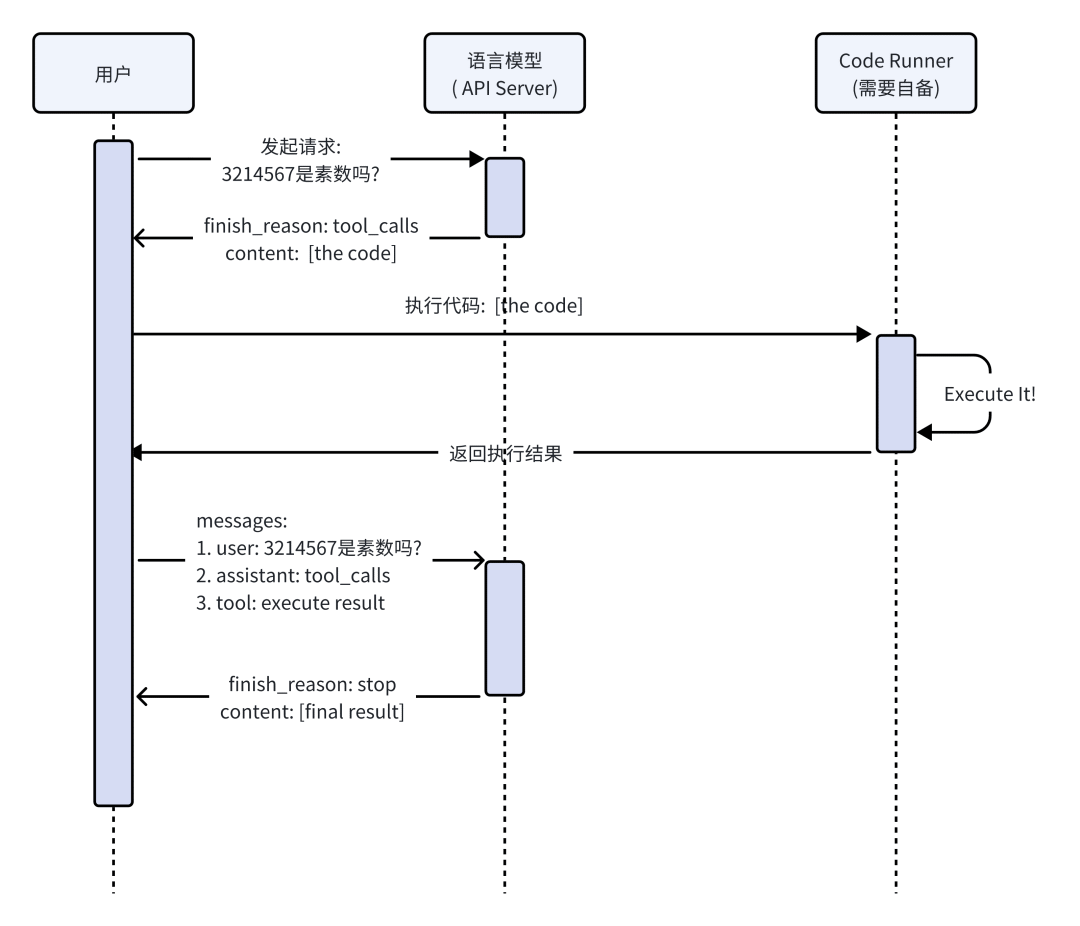
其他模型:
除此之外,字节的豆包大模型、上海人工智能实验室的InternLM2-Chat模型、百度的文心EB系列模型也支持Function Calling的功能,能够让用户通过这些模型来进行Function Calling类智能体的设计;
2.2. 各大框架对ReACT和FC的支持
Langchain
在OpenAI更新了Function Calling功能之后,LangChain也将其集成到了智能体应用的设计当中,并提供了专门的框架来支持这类Function Calling功能。Langchain的Function Calling技术允许模型在需要时调用一个或多个工具,并使用适当的输入进行响应。这种技术的核心在于API调用,通过描述工具并让模型智能地选择输出结构化对象,例如包含调用这些工具参数的JSON,从而实现更可靠、有效的工具调用。Langchain的Function Calling具有多个显著特点。首先,它支持将多个工具绑定到调用聊天模型的工具上,并允许模型选择调用哪个工具。这种灵活性使得智能体可以重复调用工具并接收结果,直到查询得到解决。其次,Langchain的Function Calling采用了ToolCall接口,以支持更广泛的提供者实现,包括Anthropic、Google Gemini和Mistral等。这种兼容性使得Langchain的Function Calling具有更广泛的应用场景。
LangChain的react方式智能体构建属于原教旨主义,是最早一批将react推理模式运用与实际应用开发中的框架;而现在langchain也没有放弃ReACT形式的智能体结构,在Langsmith中,提供了更加可视化的ReACT智能体应用的设计和测试方法,并突出了其规划的部分
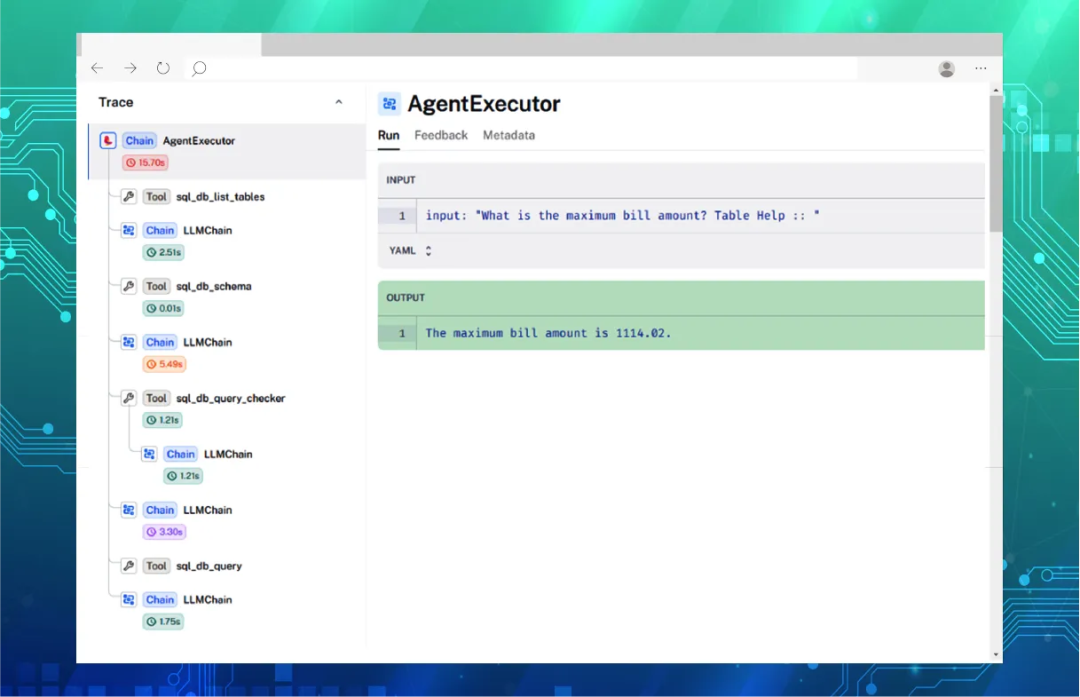
LangChain的LangSmith平台,是一个智能体应用的开发平台和框架
Dify
Dify的Function Calling与ReAct智能体框架是自然语言处理领域两项重要的技术方向。Function Calling允许模型调用一个或多个工具,并使用适当的输入进行响应,从而实现更可靠、有效的工具调用。而ReAct则通过观察环境状态并生成相应的反应来与环境交互,适用于处理动态环境和复杂交互场景。Dify为AI代理提供了50多个内置工具,如Google Search、DELL·E、Stable Diffusion和WolframAlpha,使得这两项技术在实际应用中具有广泛的应用场景和高度的灵活性。
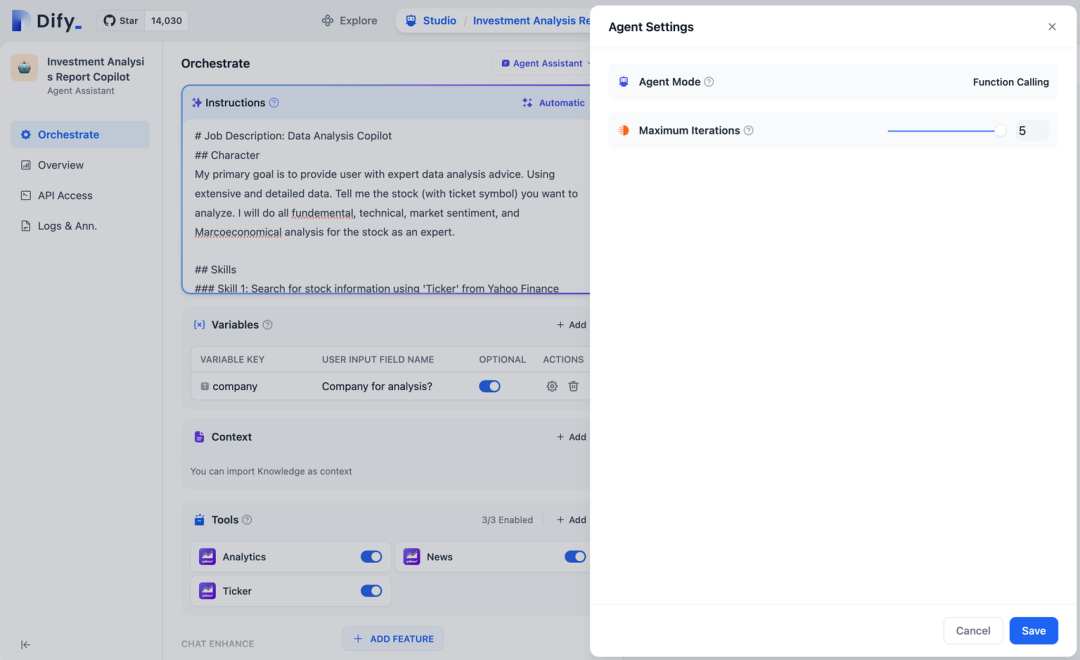
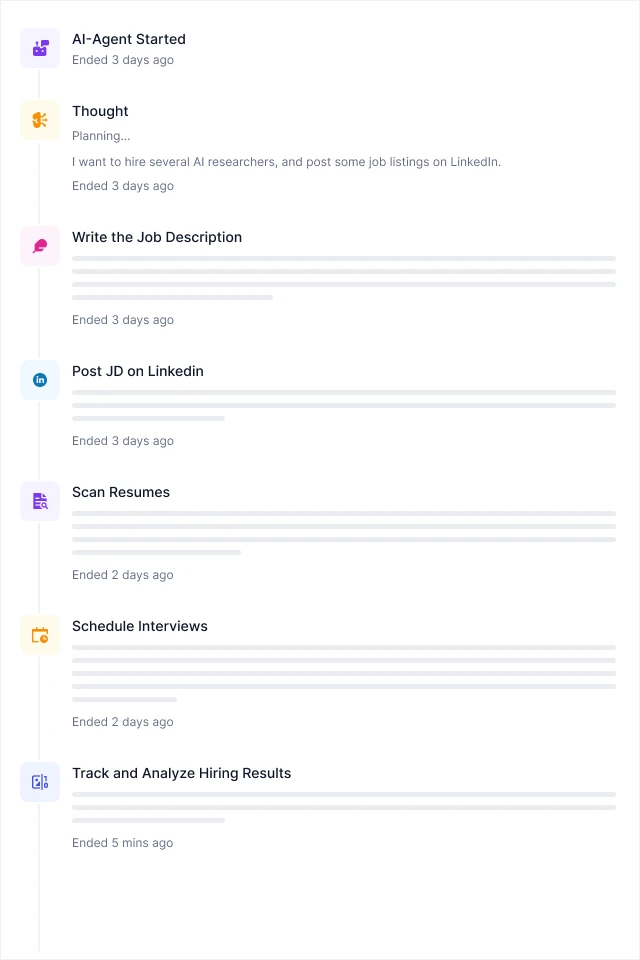
LLaMAindex
LLaMAIndex是一个全面的智能体框架,为用户提供自动推理和决策的能力。其能够接受用户的输入或查询,通过内部决策来执行查询,并返回正确的结果。LLaMAIndex的关键组件包括将复杂问题分解为较小的问题、选择和使用外部工具、规划任务序列以及将已完成任务存储在内存模块中。
在LLaMAIndex中,Function Calling和ReACT是两种主要的智能体结构类型。Function Calling代理可以与任何调用大型语言模型(LLM)的函数集成,这使其能够利用LLM大模型强大能力来执行各种任务。而ReACT代理则可以在任何聊天或文本完成端点中工作,通过跨端点的方式来实现更复杂的任务。
除此之外,LLaMAIndex通过提供高级工具和低级组件,使得构建和调试代理变得更加容易,核心代理成分如查询规划、工具使用等,也可以作为独立模块使用,进一步增强了其灵活性和可扩展性。
其他智能体框架
除此之外还有类似于Simpleaichat、Outlines、AgentGPT、AutoChain这类的智能体开发框架,但大部分活跃于去年,现在其中很多框架都已不在更新;
总结
智能体应用的开发逐渐成为了各个大模型应用开发平台所关注的重点,无论是ReACt类型的框架,还是Function Calling类型的模型,都在以难以想象的速度不断迭代。在未来几个月,可以确定是智能体应用的开发方法仍然会进一步演变,直到我们找到真正的智能体应用开发范式,能够放心地将工作中的琐事交给AI,从而把精力放在我们真正感兴趣的事情上。
如何系统的去学习大模型LLM ?
作为一名热心肠的互联网老兵,我意识到有很多经验和知识值得分享给大家,也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑,所以在工作繁忙的情况下还是坚持各种整理和分享。
但苦于知识传播途径有限,很多互联网行业朋友无法获得正确的资料得到学习提升,故此将并将重要的 AI大模型资料 包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。
😝有需要的小伙伴,可以V扫描下方二维码免费领取🆓

一、全套AGI大模型学习路线
AI大模型时代的学习之旅:从基础到前沿,掌握人工智能的核心技能!

二、640套AI大模型报告合集
这套包含640份报告的合集,涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师,还是对AI大模型感兴趣的爱好者,这套报告合集都将为您提供宝贵的信息和启示。

三、AI大模型经典PDF籍
随着人工智能技术的飞速发展,AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型,如GPT-3、BERT、XLNet等,以其强大的语言理解和生成能力,正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

四、AI大模型商业化落地方案

阶段1:AI大模型时代的基础理解
- 目标:了解AI大模型的基本概念、发展历程和核心原理。
- 内容:
- L1.1 人工智能简述与大模型起源
- L1.2 大模型与通用人工智能
- L1.3 GPT模型的发展历程
- L1.4 模型工程
- L1.4.1 知识大模型
- L1.4.2 生产大模型
- L1.4.3 模型工程方法论
- L1.4.4 模型工程实践 - L1.5 GPT应用案例
阶段2:AI大模型API应用开发工程
- 目标:掌握AI大模型API的使用和开发,以及相关的编程技能。
- 内容:
- L2.1 API接口
- L2.1.1 OpenAI API接口
- L2.1.2 Python接口接入
- L2.1.3 BOT工具类框架
- L2.1.4 代码示例 - L2.2 Prompt框架
- L2.2.1 什么是Prompt
- L2.2.2 Prompt框架应用现状
- L2.2.3 基于GPTAS的Prompt框架
- L2.2.4 Prompt框架与Thought
- L2.2.5 Prompt框架与提示词 - L2.3 流水线工程
- L2.3.1 流水线工程的概念
- L2.3.2 流水线工程的优点
- L2.3.3 流水线工程的应用 - L2.4 总结与展望
- L2.1 API接口
阶段3:AI大模型应用架构实践
- 目标:深入理解AI大模型的应用架构,并能够进行私有化部署。
- 内容:
- L3.1 Agent模型框架
- L3.1.1 Agent模型框架的设计理念
- L3.1.2 Agent模型框架的核心组件
- L3.1.3 Agent模型框架的实现细节 - L3.2 MetaGPT
- L3.2.1 MetaGPT的基本概念
- L3.2.2 MetaGPT的工作原理
- L3.2.3 MetaGPT的应用场景 - L3.3 ChatGLM
- L3.3.1 ChatGLM的特点
- L3.3.2 ChatGLM的开发环境
- L3.3.3 ChatGLM的使用示例 - L3.4 LLAMA
- L3.4.1 LLAMA的特点
- L3.4.2 LLAMA的开发环境
- L3.4.3 LLAMA的使用示例 - L3.5 其他大模型介绍
- L3.1 Agent模型框架
阶段4:AI大模型私有化部署
- 目标:掌握多种AI大模型的私有化部署,包括多模态和特定领域模型。
- 内容:
- L4.1 模型私有化部署概述
- L4.2 模型私有化部署的关键技术
- L4.3 模型私有化部署的实施步骤
- L4.4 模型私有化部署的应用场景
学习计划:
- 阶段1:1-2个月,建立AI大模型的基础知识体系。
- 阶段2:2-3个月,专注于API应用开发能力的提升。
- 阶段3:3-4个月,深入实践AI大模型的应用架构和私有化部署。
- 阶段4:4-5个月,专注于高级模型的应用和部署。
这份完整版的大模型 LLM 学习资料已经上传CSDN,朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】
😝有需要的小伙伴,可以Vx扫描下方二维码免费领取🆓

