苏州高新区网站建设建筑网图集

👀樊梓慕:个人主页
🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C++》《Linux》
🌝每一个不曾起舞的日子,都是对生命的辜负
目录
前言
1.进程创建
2.进程终止
2.1探究main函数返回值
2.2探究普通函数退出的执行情况
2.3进程退出的场景
2.4进程退出的方式
2.4.1main函数返回
2.4.2调用exit()
2.4.3调用_exit()
2.4.4exit与_exit的区别
2.4.5exit与_exit的关系
3.进程等待
3.1进程等待的必要性
3.2进程等待的方法
3.2.0输出型参数status
3.2.1wait方法
3.2.2waitpid方法
4.进程程序替换
4.1什么是进程程序替换?
4.2进程程序替换的细节
4.3进程程序替换的函数
4.2.1execl
4.2.1execlp
4.2.2execv
4.2.3execvp
4.2.4exec*可以执行系统的指令(程序),可以执行我们自己编写的程序么?
4.2.5execle
4.2.6execvpe
4.2.7execve
前言
本篇文章博主将会与大家共同学习进程控制的相关内容,快来一起学习吧。
欢迎大家📂收藏📂以便未来做题时可以快速找到思路,巧妙的方法可以事半功倍。
=========================================================================
GITEE相关代码:🌟fanfei_c的仓库🌟
=========================================================================
1.进程创建
进程创建的大部分内容其实我们已经在之前的文章就介绍的差不多了,比如fork函数创建子进程,fork函数的返回值的意义,以及写时拷贝等等,所以如果对这部分由疑问的话,大家可以到我的Linux专栏中找到进程概念了解fork函数的相关内容,找到进程地址空间了解写时拷贝的内容,这部分我就不再重复了。
樊梓慕-Linux专栏![]() http://t.csdnimg.cn/piqro
http://t.csdnimg.cn/piqro
2.进程终止
2.1探究main函数返回值
main函数的返回值是返回给谁的?
你可能会说是main函数的上层函数,但其实最终是通过加载器被操作系统调用的,也就是说main函数的返回值最终还是会给给操作系统,操作系统会读取main函数的返回值来检测进程的执行情况。
其实main函数的返回值具有特殊意义。
main函数的返回值叫做进程的退出码。
我们可以利用main函数不同的返回值表示不同的失败原因。
- 当返回0时,代表进程执行成功。
- 当返回其他非0数字时,代表着不同的错误原因。
我们可以用echo $?的指令来获取最近一次执行的进程的退出码:
比如:

注意:指令也是进程,只要是进程就会有退出码,所以只要你输入的指令正常执行了,查询到的退出码也是0。
 另外我们可以将退出码转化成为进程执行是否顺利的信息。
另外我们可以将退出码转化成为进程执行是否顺利的信息。
当然执行成功我们不需要知道为什么成功,只需要知道失败为什么而失败。
所以我们可以使用语言和系统自带的一些方法,进行转化:
比如在之前学习C语言时strerror函数可以通过退出码获取该退出码对应的错误信息:
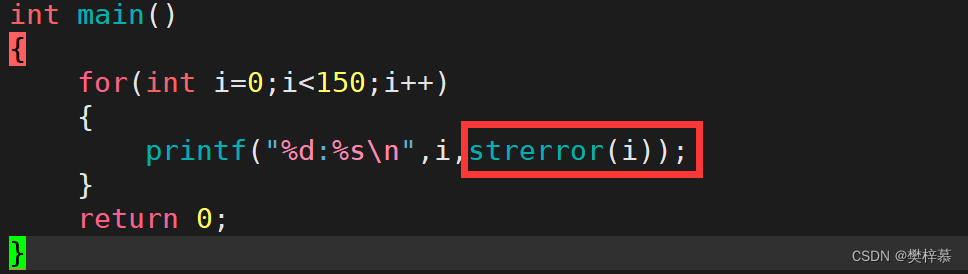
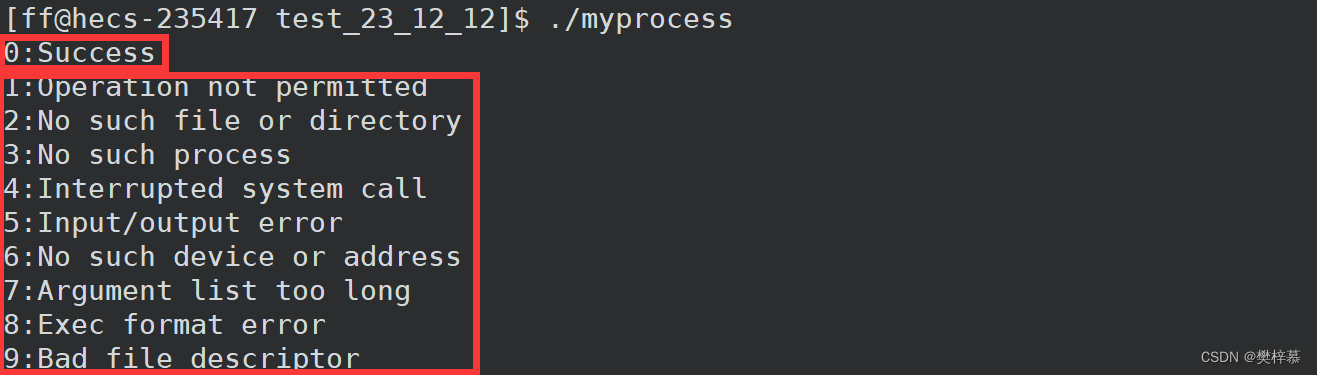
当然我们也可以自己设置退出码的字符串含义。
注意:其他函数退出,仅仅表示函数调用完毕。
2.2探究普通函数退出的执行情况
前面说普通函数退出,仅表示调用完毕,那我们怎么知道函数的执行情况呢?
调用函数,我们通常想看到两种结果:
- 函数的执行结果;
- 函数的执行情况。
比如fopen函数,当他成功时返回的是文件指针,失败时返回NULL,但我们如何知道更多有关失败的信息呢?

所以当fopen失败时会有错误码errno被设置,如:
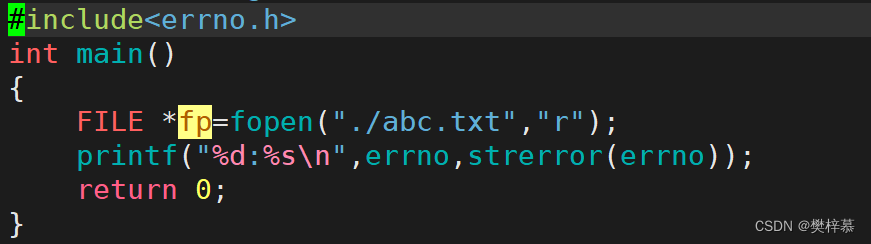

注意:这里的函数都指的是库函数,我们自己定义的函数在退出时不会有错误码被设置,当然你可以自己设计。
2.3进程退出的场景
- 代码运行完毕,结果正确
- 代码运行完毕,结果不正确
- 代码异常终止
我们肯定要先确定代码会不会有异常,然后再去看结果是否正确。(异常之后,退出码无意义)
所以什么是异常?
异常的本质实际上就是进程收到了异常信号。
我们模拟一下:
kill -l查看信号: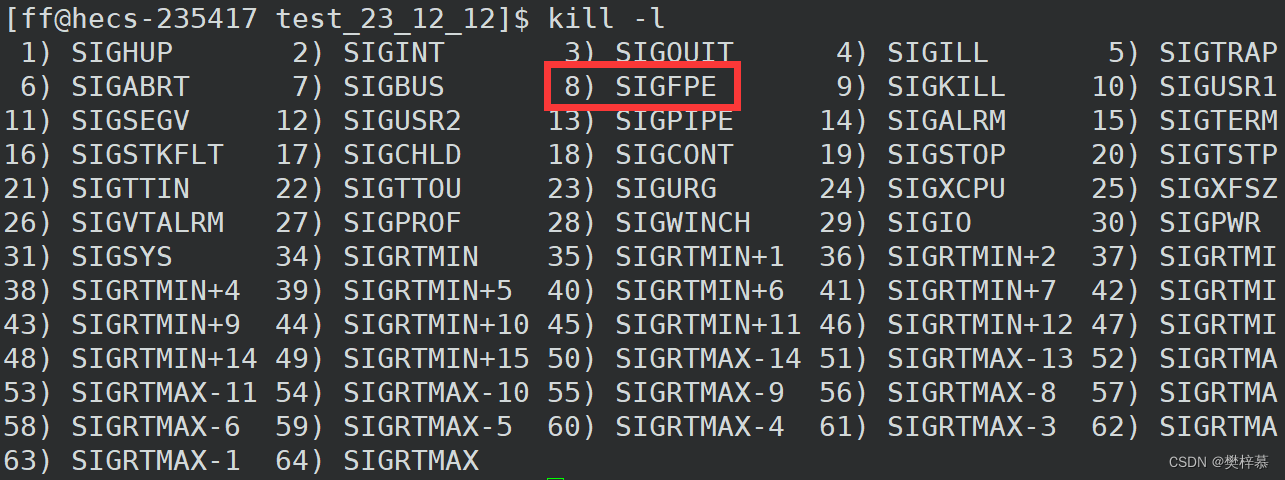 我们向该进程发送8号信号:
我们向该进程发送8号信号:

所以说异常就是进程收到了异常信号。
另外每个信号都有自己对应的编号,后面的内容是数字的宏名称。
所以不同的信号编号对应着不同的异常原因。
结论:进程最终的执行情况可用两个数字来表示,这两个数字一个为信号编号,一个为退出码。
2.4进程退出的方式
2.4.1main函数返回
我们可以用main函数return的方式退出进程。
2.4.2调用exit()
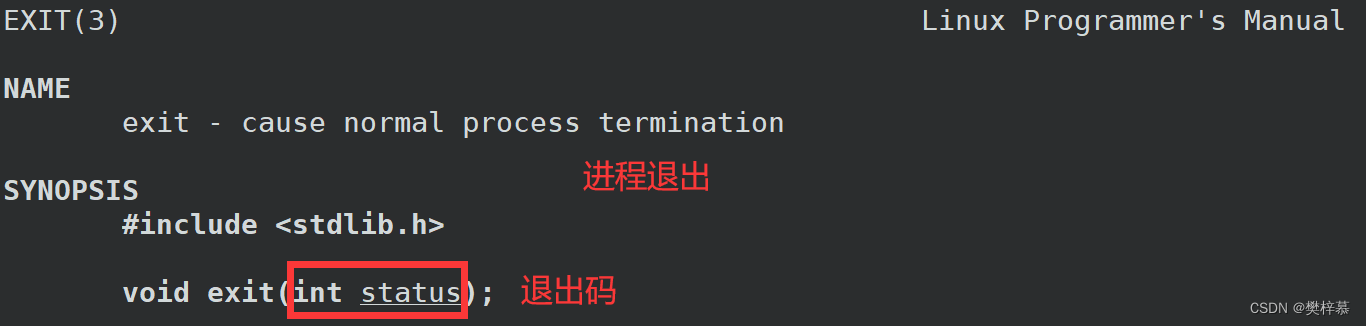
exit就是用来终止进程的,status代表着退出码,在我们的进程代码中,任意地方调用exit,都表示进程退出。
2.4.3调用_exit()
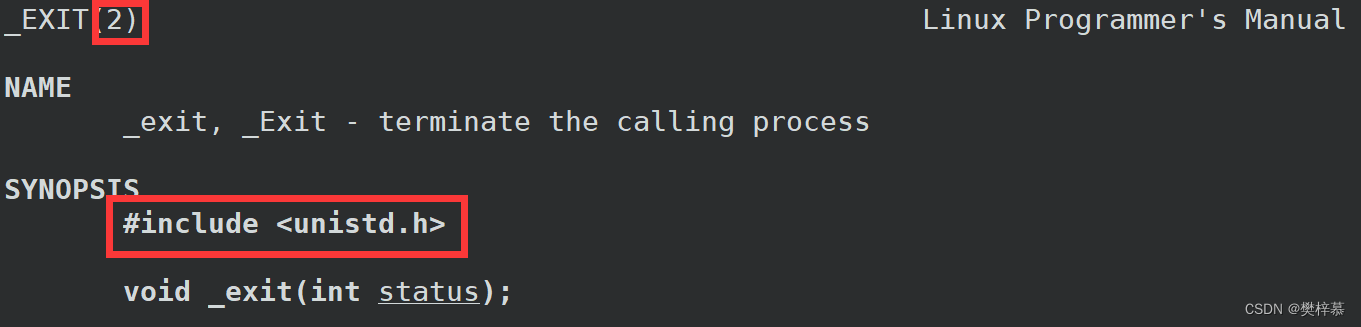
_exit属于2号手册,是系统调用,但也是可以用作终止进程。
2.4.4exit与_exit的区别
exit支持刷新缓冲区,_exit不支持刷新缓冲区!
什么意思呢?
首先:要知道利用printf打印内容时如果不加\n,该内容不会立即刷新出来,而是处在缓冲区内。
有了这个基础我们就来验证一下:
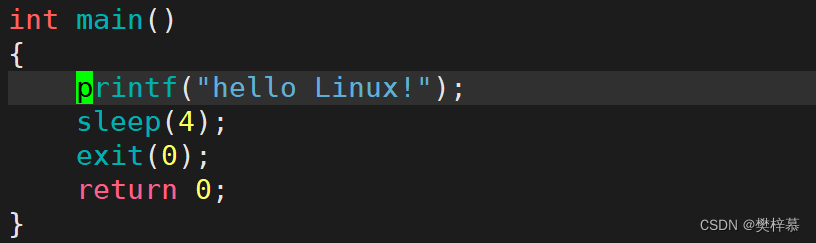
 我们发现四秒后执行exit,缓冲区内的内容仍然被刷新了出来,所以exit支持刷新缓冲区!
我们发现四秒后执行exit,缓冲区内的内容仍然被刷新了出来,所以exit支持刷新缓冲区!
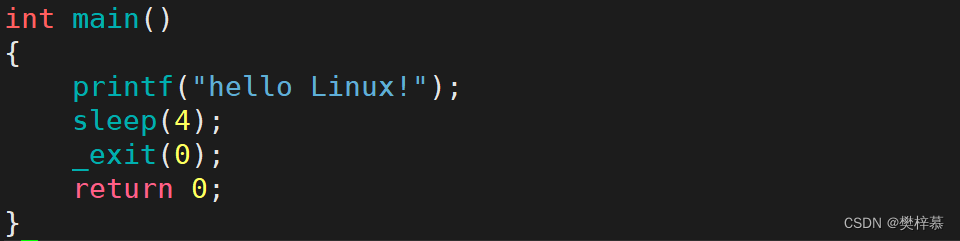
 我们发现四秒后执行_exit,缓冲区内的内容并没有刷新出来,所以_exit不支持刷新缓冲区!
我们发现四秒后执行_exit,缓冲区内的内容并没有刷新出来,所以_exit不支持刷新缓冲区!
2.4.5exit与_exit的关系
谁才有资格终止进程??
只有操作系统才能够终止进程,所以想要终止进程必须要调用系统调用_exit,所以exit的底层就是封装的_exit。
- 扩展:printf和scanf属于库函数,有资格对硬件写入么??所以printf和scanf的底层也必然封装了系统调用接口
思考:为什么要有exit这样的库函数封装系统调用接口,直接使用系统调用接口不好么?
首先语言要封装肯定是有要满足语言的特性或者为了简化使用系统调用的成本,但这些我们今天不考虑。
语言是如何具有跨平台性的?
不同的系统他们的系统调用肯定是不一样的,所以语言就对这些系统调用做了封装,从而在库的层面上把底层的差异化通过库的封装给屏蔽掉了!
3.进程等待
3.1进程等待的必要性
之前讲过,子进程退出,父进程如果不管不顾,就可能造成‘僵尸进程’的问题,进而造成内存泄漏。
另外,进程一旦变成僵尸状态,那就刀枪不入,kill -9 也无能为力,因为谁也没有办法杀死一个已经死去的进程。
最后,我们需要知道父进程派给子进程的任务完成的如何。
父进程通过进程等待的方式,回收子进程资源,获取子进程退出信息。
3.2进程等待的方法
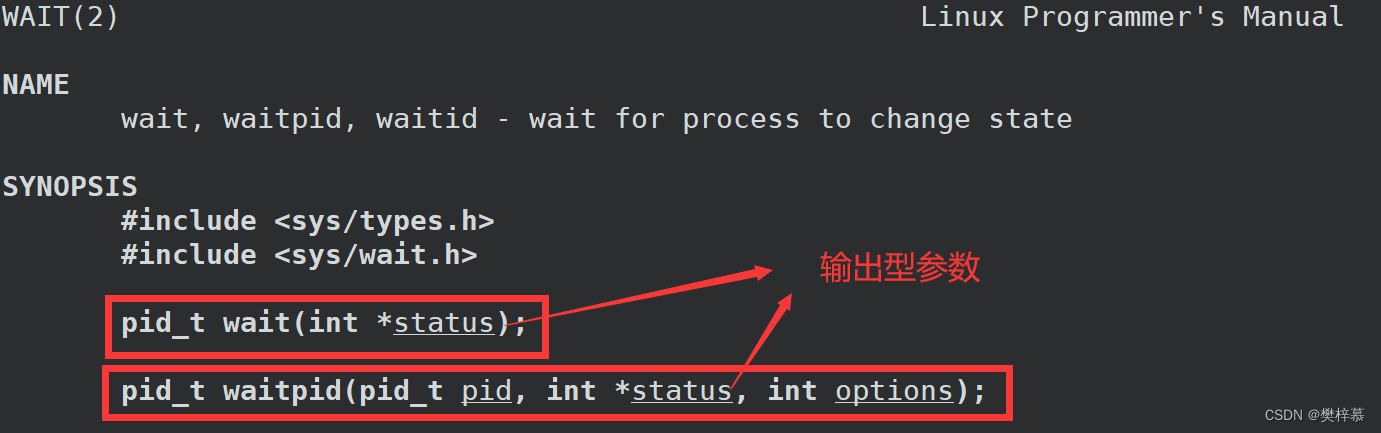
3.2.0输出型参数status
进程等待所用的两个函数wait和waitpid,都有一个status参数,该参数是一个输出型参数,由操作系统进行填充。
如果不关心子进程的退出状态信息,则可以对status参数传入NULL。否则,操作系统会通过该参数,将子进程的退出信息反馈给父进程。
status是一个整型变量,但status不能当作整型来看待,status的不同比特位所代表的信息不同,具体细节如下(这里我们只研究status低16比特位):
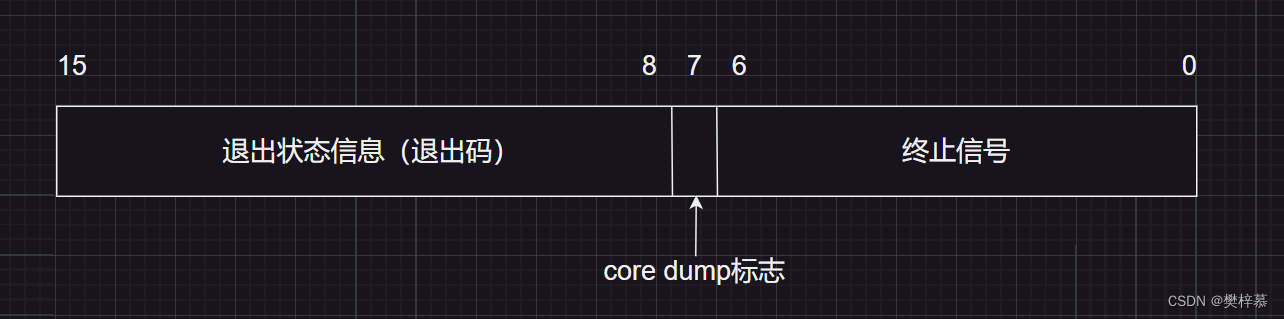
如图所示0-6位的七个比特位代表终止信号,而8-15位的八个比特位代表退出状态信息,这也刚好说明了:进程最终的执行情况可用两个数字来表示。
那我们可以尝试通过对status进行位操作来获取下终止信号和退出码:
exitCode = (status >> 8) & 0xFF; //退出码
exitSignal = status & 0x7F; //退出信号那我们每次都需要通过位操作来获取这两个数字么??
系统当中提供了两个宏来获取退出码和退出信号。
- WIFEXITED(status):若为正常终止子进程返回的状态则为真(查看进程是否正常退出)W(wait) IF(if) EXITED(正常退出)
- WEXITSTATUS(status):若WIFEXITED为零则提取子进程的退出码。(查看进程的退出码)W(wait) EXIT(exit) STATUS(状态)
exitNormal = WIFEXITED(status); //是否正常退出
exitCode = WEXITSTATUS(status); //获取退出码3.2.1wait方法
pid_t wait(int *status)等待任意一个子进程直到父进程读取到子进程的退出信息(阻塞等待),默认为阻塞等待。
返回值:
- 成功返回等待的子进程pid,失败返回-1。
参数:
- status:若不关心子进程的退出状态信息,则可以对status参数传入NULL。
3.2.2waitpid方法
pid_t waitpid(pid_t pid,int *status,int options);返回值:
- 等待成功返回被等待进程的pid。
- 如果设置了选项
WNOHANG,而调用中waitpid发现没有已退出的子进程可收集,则返回0。 - 如果调用中出错,则返回-1,这时errno会被设置成相应的值以指示错误所在。
参数:
- 当参数pid=-1时,则等待任意子进程。
- 当参数pid>0时,等待进程标识符为pid的子进程。
- status:若不关心子进程的退出状态信息,则可以对status参数传入NULL。
- 当options=0时,为阻塞等待。
- 当options=
WNOHANG时,为非阻塞等待,即父进程检测到子进程没有退出会立即返回0不会一直等待什么也不做(操作系统会循环式的检测子进程是否退出,这叫做基于非阻塞的轮询访问),而如果返回值小于0则代表等待失败,大于0代表等待成功并返回被等待进程的pid。 - 非阻塞等待的优点是:轮询期间不要傻傻的等着,可以做做其他事情。
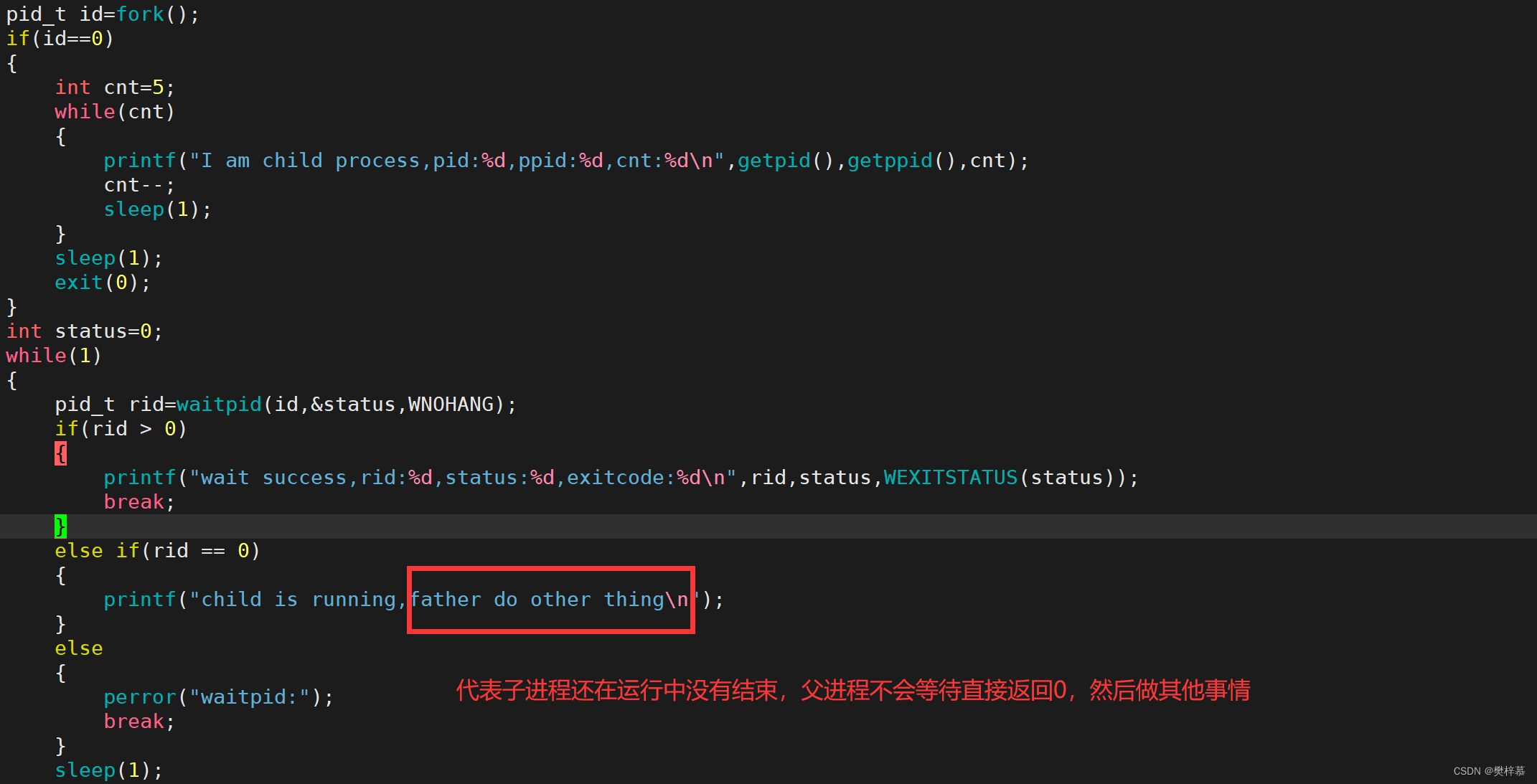
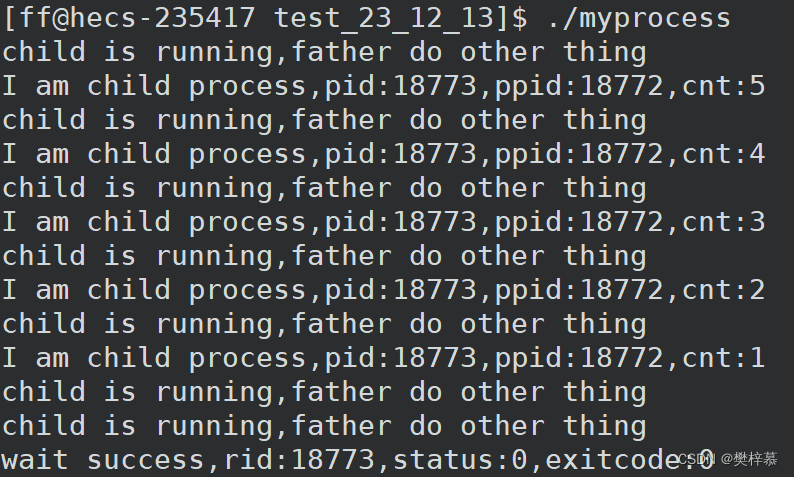
小贴士:HANG其实就是一种死机的说法,所以这里的WNOHANG可以记为W(wait) NO(no) HANG。
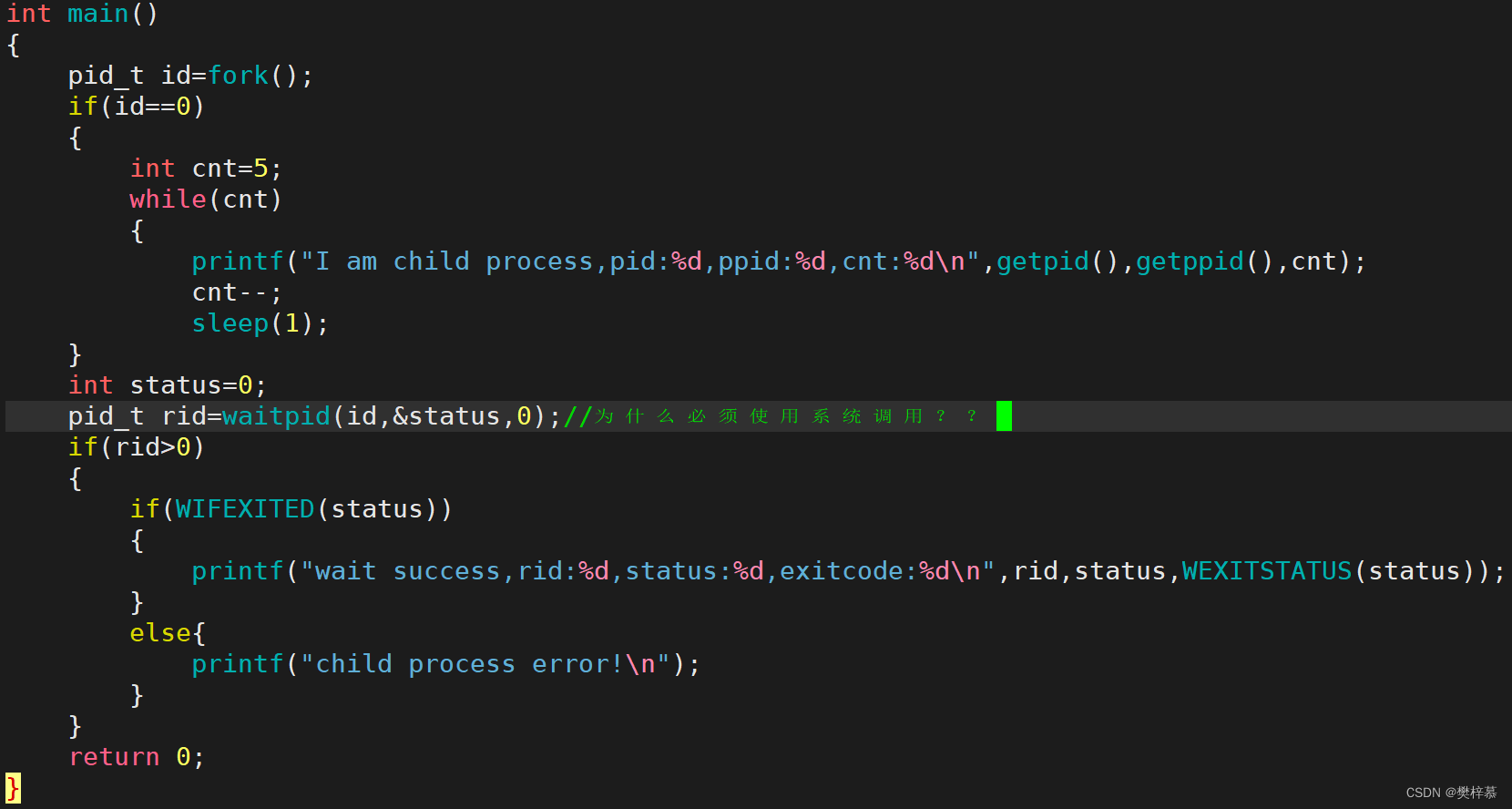
思考:为什么需要waitpid这个系统调用来获取进程的退出码和信号?
利用两个全局变量,当进程哪里出问题时,我自己修改全局变量的值改成对应的退出码和信号不就行了么?
注意:进程独立性!!
- 因为全局变量属于父进程,子进程要对该共享变量修改,会发生写时拷贝,子进程退出时,父进程接收不到修改后的信息,进程的独立性!!
所以必须需要系统调用,当子进程退出时,会释放掉进程地址空间、页表等,只留一个PCB,PCB中会保存这两个数字,所以当父进程回收子进程时,通过系统调用waitpid(注意:父进程不能直接访问子进程的PCB,这也是通过系统调用才能拿到的,操作系统不相信任何人)就能拿到退出进程的退出码和信号了,此时才可以将这两个数字写入到整型变量status!
4.进程程序替换
4.1什么是进程程序替换?
我们创建的子进程可以执行其他程序的代码么?
可以,这就需要用到进程程序替换的知识了。
若想让子进程执行另一个程序,需要调用一种exec函数。
当进程调用exec函数时,该进程的物理内存上的代码和数据完全被新程序替换,并从新程序的启动例程开始执行。
也就是说不影响进程PCB、进程地址空间和页表,将替换执行的程序的代码和数据覆盖到原来的进程物理内存上!
思考:进程程序替换时,有没有创建新的进程?
不会,只是进程在物理内存中的代码和数据发生了改变,进程的PCB、进程地址空间、页表都没有改变,所以并没有创建新的进程。
思考:子进程进行进程程序替换会不会影响父进程的代码和数据?
不会,当检测到子进程进行进程程序替换时会发生写时拷贝(因为对之前父子共享的代码和数据进行了修改(写入),所以会发生写时拷贝),此后父子进程的代码和数据也就分离了,所以子进程进行进程程序替换后不会影响父进程的代码和数据。
4.2进程程序替换的细节
- 程序替换一旦成功,原来的后续的代码将不会执行,因为被替换掉了。
- 进程程序替换接口只有失败返回值,没有成功返回值。(因为如果成功代表着程序被替换掉了)
- 替换完成,不创建新的进程。
- 进程程序替换接口其实就是扮演的加载器的角色,如果没有要替换的程序就是加载。(将程序加载到内存)。
4.3进程程序替换的函数
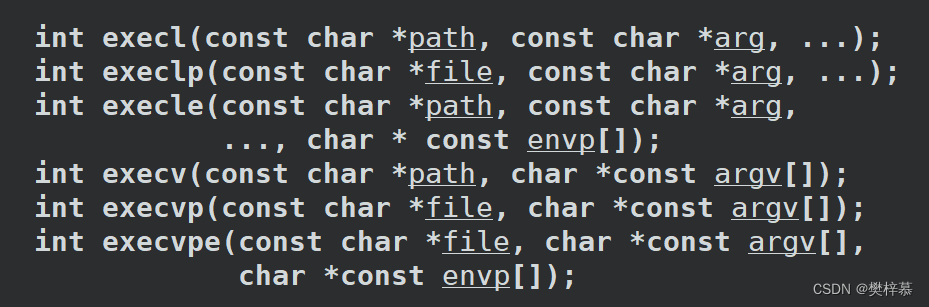
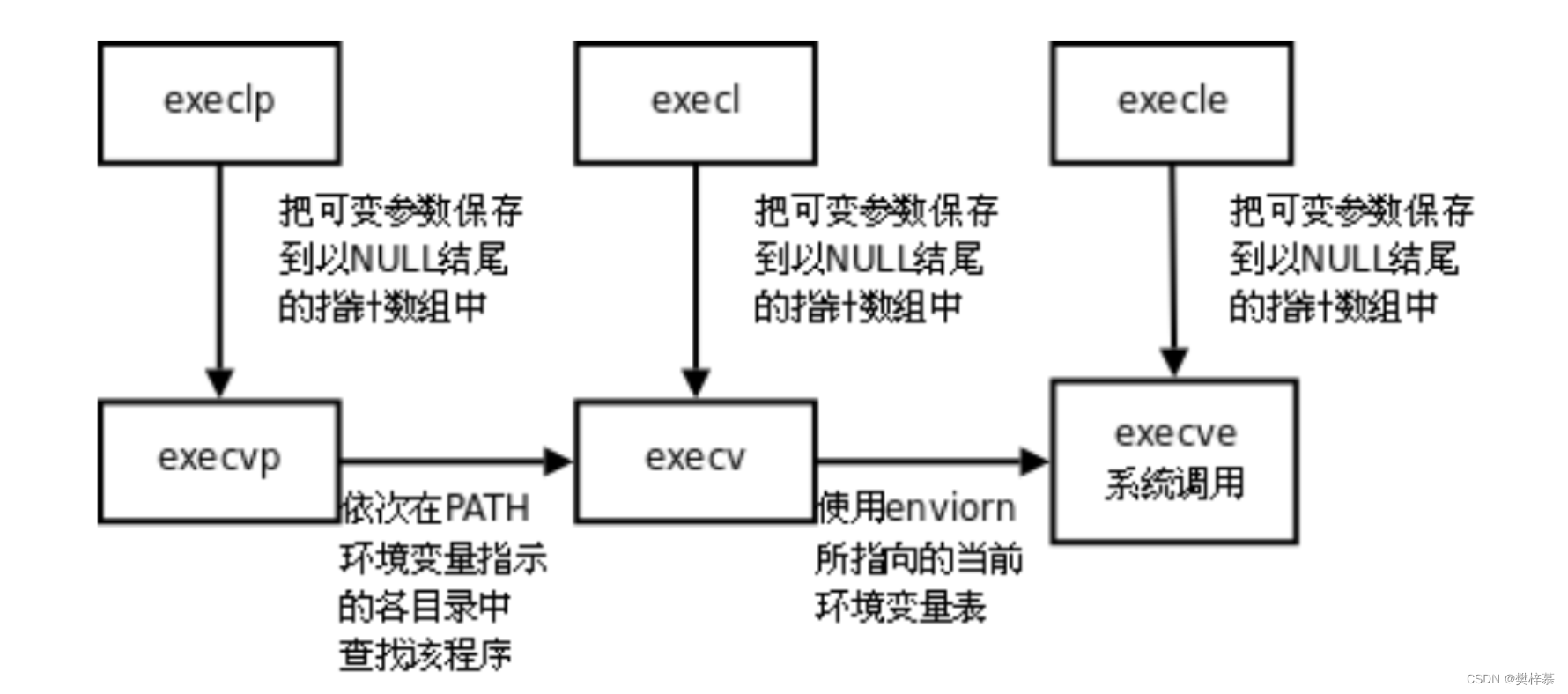
我们发现进程程序替换函数都是exec+p/l/v/e。他们分别暗指什么意思呢?
函数名中'p'的含义(PATH):
- 程序替换函数中名字带'p'的参数一般传程序的名字即可,他会自己到环境变量PATH的路径下查找该程序。
- 名字不带'p'的参数一般传绝对路径。
函数名中'l'和'v'的含义(list/vector):
- 名字中带'l'的,一般后面的参数是以列表list形式呈现的,如
execl("/usr/bin/ls","ls","-a","-l",NULL);- 名字中带'v'的,一般后面的参数是以数组vector形式呈现的,如
char* myargv[] = { "ls", "-a", "-i", "-l", NULL };
execv("/usr/bin/ls", myargv);函数名中'e'的含义(环境变量):
- 名字中带'e'的,一般表示可以给替换后的程序传递全新的环境变量表。
4.2.1execl
int execl(const char *path, const char *arg, ...);//...为可变参数,可类比printf函数参数:
- const char *path:程序的路径
- const char *arg:要进行的操作,可变参数列表
实例:
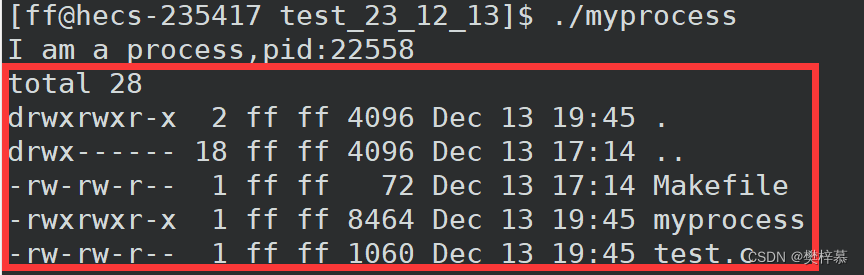
4.2.1execlp
int execlp(const char *file, const char *arg, ...);参数:
- const char *file:程序名称
- const char *arg:要进行的操作,可变参数列表
实例:
execlp("ls", "ls", "-a", "-l", NULL);4.2.2execv
int execv(const char *path, char *const argv[]);参数: 略。
实例:
char* myargv[] = {"ls", "-a", "-l", NULL};
execv("/usr/bin/ls", myargv);4.2.3execvp
int execvp(const char *file, char *const argv[]);参数:略。
实例:
char* myargv[] = {"ls", "-a", "-l", NULL};
execvp("ls", myargv);4.2.4exec*可以执行系统的指令(程序),可以执行我们自己编写的程序么?
首先我们来插一句题外话
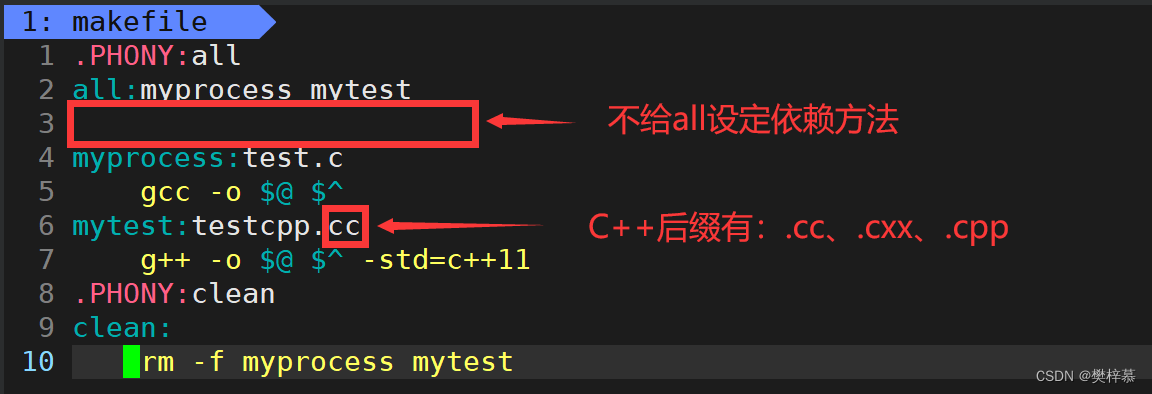
makefile如何写可以在make时对两个文件进行编译链接形成两个可执行程序呢?
我们知道makefile从上到下进行扫描时默认只会生成一个可执行程序(从上往下第一个)。
那如何处理呢?
因为all依赖于myprocess和mytest,所以这两个必然会被生成,但是不给all依赖方法,也就是说啥也不干,所以就能形成两个可执行程序了。
写一段C++代码,一会做程序替换用:
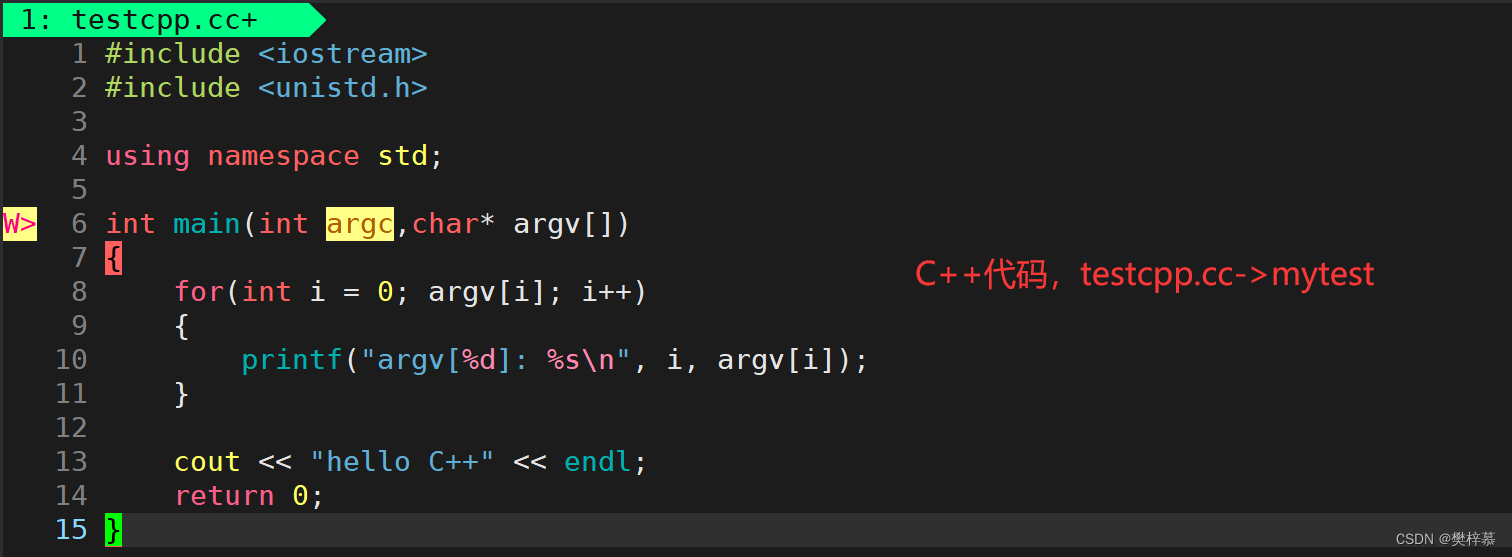
测试用函数:
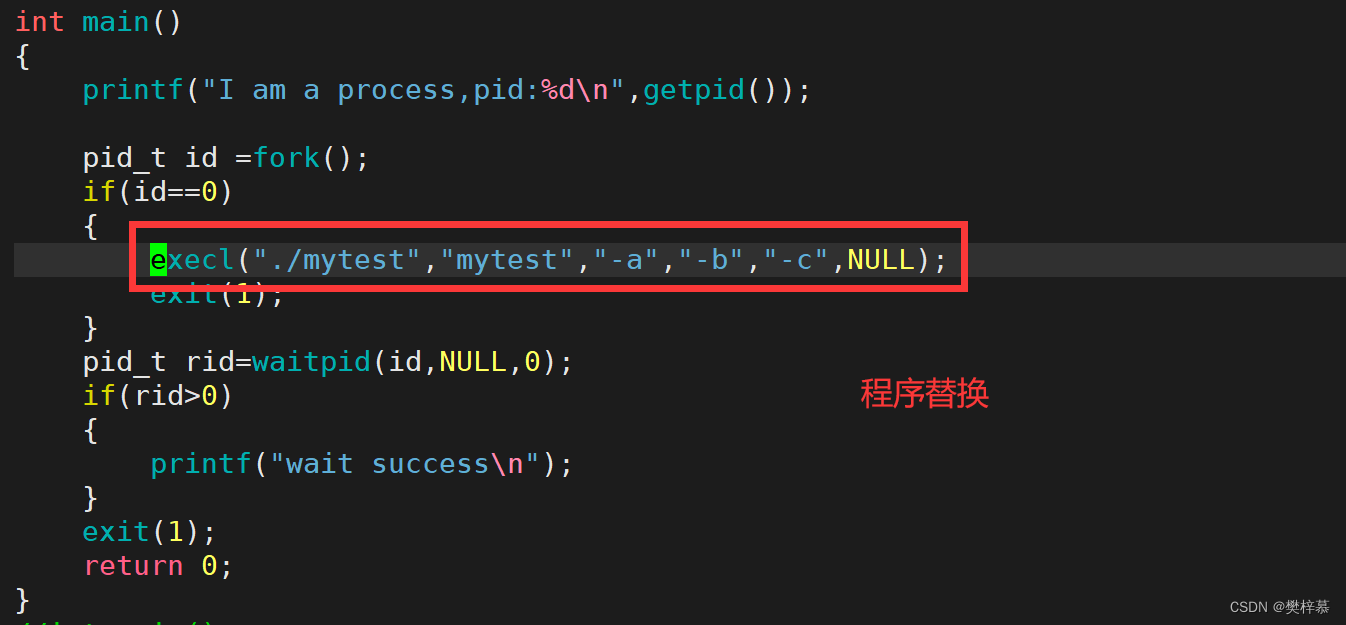
通过执行myprocess,就能观察到替换后的执行情况:
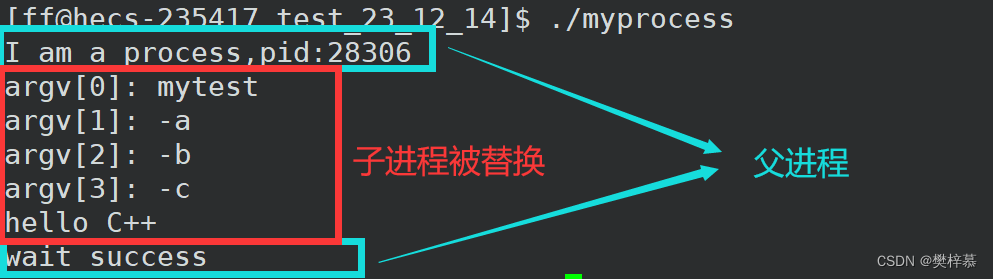
所以可以执行我们自己编写的程序,无论是什么语言(因为最终都会生成可执行程序)。
根据上面的例子我们发现进程替换时传递了命令行参数,那环境变量参数呢?其实有这样的参数可以给替换后的程序传递全新的环境变量信息。(注:子进程和替换后的进程用的同一个进程地址空间,所以环境变量依旧会被继承下去,虽然替换后代码和数据会写时拷贝,但环境变量部分不受影响)
接下来我们学习另外两个程序替换函数:
4.2.5execle
int execle(const char *path, const char *arg, ..., char *const envp[]);参数:
- const char *path:程序的路径
- const char *arg:要进行的操作,可变参数列表
- char *const envp[]:要覆盖的全新的环境变量
实例: 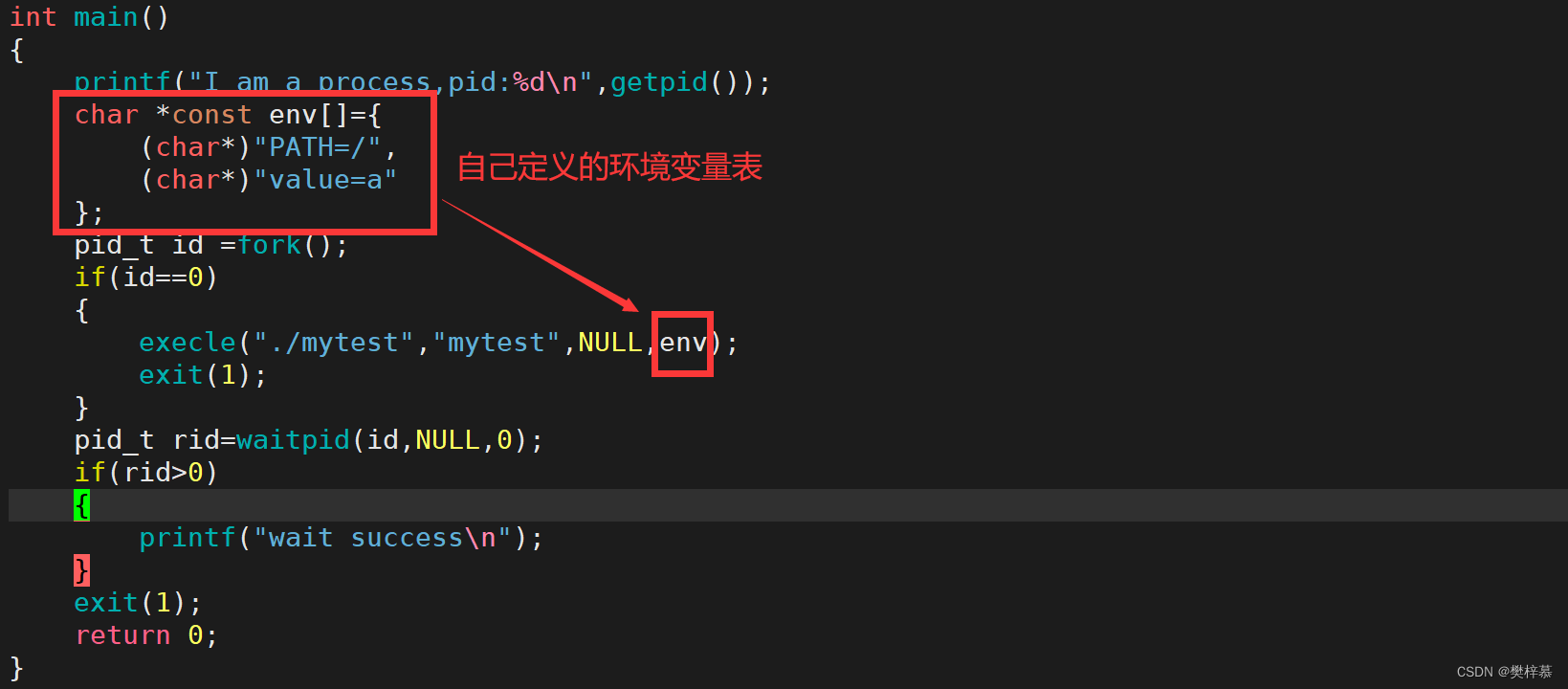
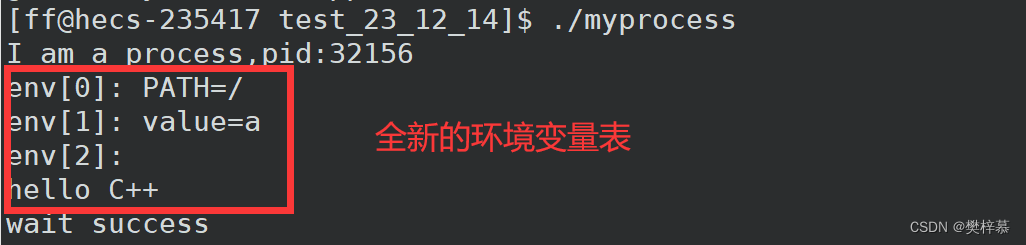
4.2.6execvpe
参数:略。
实例:
char* const env[]={"PATH=/","value=a"};
char* myargv[] = {"ls", "-a", "-l", NULL};
execvpe("ls", myargv, env);4.2.7execve
看到这你会发现以上的六种函数功能十分相似,因为他们都是由execve这个系统调用封装而来的!
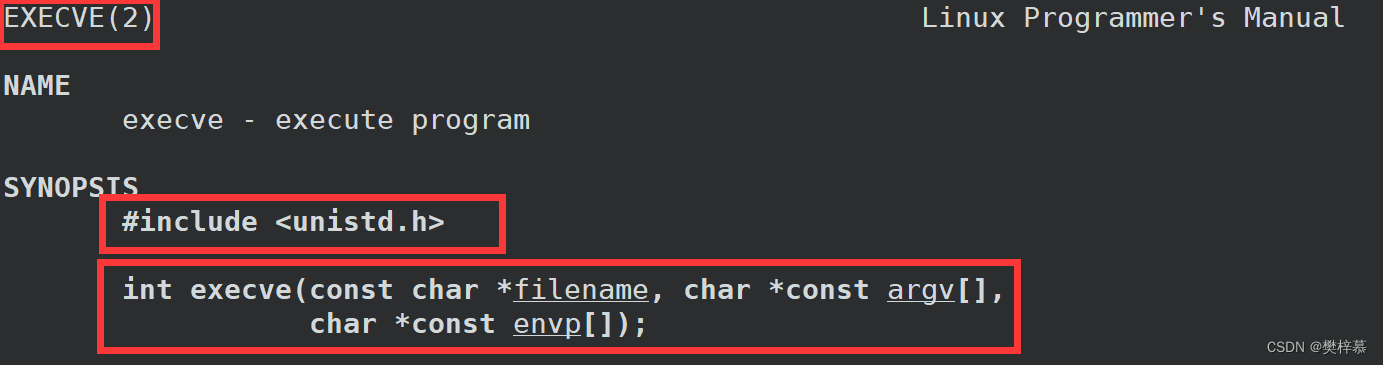
=========================================================================
如果你对该系列文章有兴趣的话,欢迎持续关注博主动态,博主会持续输出优质内容
🍎博主很需要大家的支持,你的支持是我创作的不竭动力🍎
🌟~ 点赞收藏+关注 ~🌟
=========================================================================