昆山网站建设机构溧阳市城乡建设局网站
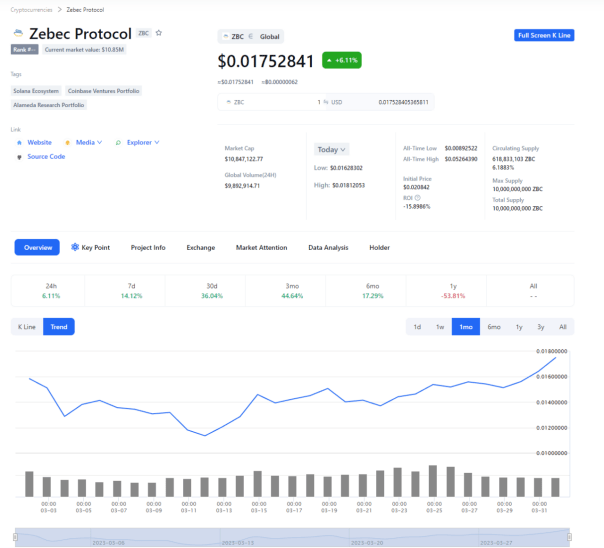
近期,ZBC通证迎来了新一轮上涨趋势,我们看到其从3月11日左右的低点$0.0115上涨至$0.0175,这也是近期的最大涨幅之一。我们看到,推动ZBC上涨的主要因素,是Zebec生态近期频繁的布局所带来的系列利好推动。
本文将对近期的利好要素进行盘点,以帮助读者进一步了解Zebec生态的发展现状。
Zebec Labs推出规模2000万美元生态基金,用于孵化 Nautilus Chain 生态
此前,Zebec 生态曾成立了 Zebec Labs ,其将以投资、孵化等形式,推动生态的发展。在近期,Zebec Labs 推出了首期规模为2000万美元生态基金,以用于 Nautilus Chain 生态的发展, Nautilus Chain 上的开发者都可以向 Zebec Labs 申请资金。

据了解,该计划分为两部分,包括 Nautilus 上启动的开发者的经济激励、在 Nautilus 上启动的社区激励措施两个部分。
l Nautilus 上启动的开发者的经济激励
1. 评审团和社区将选出前 10 名项目,并授予他们“每月船长赏金”。赏金金额从 5,000 美元到 10,000 美元不等,金额为 $ZBC,将根据金额分阶段发放。(注册将在主网启动之前开放。)
2. Nautilus Chain 上的项目在 3 个月内达到超过 5,000,000 美元的 TVL,将有机会获得生态基金提供的流动性激励。有关激励申请的详细信息将在 Nautilus 主网上线后公布。
3. 优质项目或有机会获得Modular Labs的直接投资,最高投资额为1,000,000美元,并有机会获得Modular Labs合作伙伴VC的追加跟投。
4.Zebec Labs 还将为黑客马拉松、Layer 3 学术建设和未来的 BUIDL 活动提供奖金和赞助支持。
l 在 Nautilus 上启动的社区激励措施
1. 技术支持:无论您是需要技术支持、更多人力,还是只是需要更多场地来展示您的项目,都可以从 Zebec 团队获得帮助。
2. 营销支持:Zebec 团队还将提供营销支持。Zebec Labs 可以帮助制定营销策略、增长计划、品牌和其他相关营销垂直领域,以帮助项目达到目标受众并实现业务目标。
3. 生态支持:Zebec Labs还可以帮助您与其他生态项目更紧密地合作,包括合作伙伴整合、行业知识共享等。
4. Zebec流媒体支付支持:Zebec Labs提供Zebec流媒体支付技术支持,连接支付渠道。
5. Web2 企业到 Web3 转换支持:Zebec Labs为转换解决方案提供全面的咨询支持。
目前,Poseiswap 是 Nautilus Chain 上的首个DEX,也是首个应用, Zebec Labs 目前向 Poseiswap 提供了150万美元的资助,以帮助其实现长期的发展。Zebec Labs的启动,将帮助Zebec生态实现更为可持续的发展,并逐渐走向新的繁荣。
ZBC通证也将随着生态的发展,而被赋予更多的消耗场景与应用场景。
Nautilus Chain 测试网“Triton”数据喜人
目前,Nautilus Chain 已经上线了测试网“Triton” ,允许任何用户参与测试网的交互测试,而目前该测试网上线不久,就已经得到了行业的广泛关注。
目前,根据 Nautilus Chain 官方3月31日数据显示,其测试网“Triton”上总交易量达到了324795笔,总地址数达到了30493个,参与人数达到了6142人。相较于前一日,新增交易笔数 70141、新增交互地址数 3339个以及参与新增参与人数1650人。
作为行业内首个支持开发者自由定制化的Layer 3链 ,Nautilus Chain 本身具备十分鲜明且独特的技术特点,它的几个关键的技术优势:
1. 无缝生态系统集成的模块化设计
通过将共识、计算和存储封装在不同的层中,Nautilus 链增强了可扩展性和定制性。它与 Eclipse 的集成将它连接到以太坊,并且它可以使用 Celestia 实现数据可用性 (DA)。这使得 Nautilus 可以与 EVM 链和 Cosmos 链互操作,同时保持高可扩展性。
2.EVM兼容性
作为有史以来第一个基于 Eclipse 的并行 EVM 汇总,Nautilus 与其他 EVM 链具有高度的互操作性。它还可以跨链与不同的 VM 同步数据,这是对其他第 2 层或多链 EVM 系统具有挑战性的壮举。这一成就为 Rollup 技术的发展树立了新的里程碑。
3.隐私
Nautilus 旨在提供隐私支付——迁移到 ZK-rollups 将实现更强大的隐私功能。隐私对于许多商业应用程序和 Web3 支付基础设施的大规模采用至关重要。为了进一步促进采用和合规性,Nautilus 将实施基于 ZK 的反洗钱控制,不会侵犯链上隐私。随着 Nautilus 成为全球支付系统中更重要的一部分,这将使 Nautilus 能够保护消费者并遵守审计员的要求。
4. 速度更快
与其他需要按顺序处理交易的 EVM 链不同,Nautilus 允许并行处理交易。事务的并行处理使 Nautilus 成为迄今为止最快的 EVM 链,初始 TPS 为 2,000,并且很快就会有更快的速度。
5.轻巧友好
由于其模块化设计,Nautilus 是“轻量级”的,这意味着它具有高度的互操作性、可扩展性和可定制性。将来,开发人员将能够选择在模块化链堆栈中使用哪些其他主要链,从而决定在哪些 VM 和执行层之间使用。这不仅可以帮助开发人员,还可以帮助其他链达到更高水平的性能和功能。
6. 独立性和 Web 2.0 的可扩展性
通过支持效率、安全性、隐私和合规性,Nautilus Chain 准备好将 Web3 更好地集成到 Web 2.0 世界中。这一直是 Zebec Protocol 的目标和愿景,Zebec Protocol 从一开始就致力于用区块链系统取代传统的金融基础设施。它的 Zebec Pay 工具是用于支付流的主要符合税收的工资单解决方案,由 Web3 和 We2 公司使用。Nautilus Chain 进一步实现了 Zebec 扩展 Web3 技术的愿景。
Nautilus Chain 生态的发展进展,正在为ZBC通证构建较为坚固的价值基础,而未来 Nautilus Chain 主网上线后,ZBC通证将开启极致通缩。
与万事达联手推出 Zebec Card
面对欧洲用户,Zebec Protocol 与 Mastercard 展开了新的合作,共同推出了可以用于加密支付的信用卡 Zebec Card。目前,该卡是首张基于 Solana 的支付卡,并能够在英国和欧盟的 26 个欧洲国家/地区推出后使用。
支持的具体国家包括 葡萄牙、克罗地亚、保加利亚、斯洛文尼亚、德国、法国、西班牙、波兰、比利时、希腊、芬兰、拉脱维亚、意大利、瑞典、列支敦士登、丹麦、马耳他、立陶宛、斯洛伐克、卢森堡、爱沙尼亚、挪威、匈牙利、捷克共和国(捷克)、罗马尼亚、爱尔兰。不包括奥地利、塞浦路斯共和国、冰岛和荷兰。
该卡与 Zebec 应用程序(Zebec Pay)以及基于 Solana 的钱包结合使用,使用户能够将他们的加密货币转移到卡中,并在世界任何地方使用 Mastercard 卡进行支付。Zebec Card 的持有者,可以使用其本地通证 $ZBC 通过该卡赚取高达7%的奖励。
目前,该卡持有者可以直接使用加密货币与法币的兑换,并支持使用该卡基于加密货币进行支付,以及使用该卡接受加密货币作为薪水报酬的支付,同样在Zebec 生态设施的支持下,进行流支付场景的应用。
该 Zebec Card 不收取注册费、年费或额外的兑换费,并提供最低(通常低于 1%)的交易费。英国和整个欧洲符合条件的国家/地区*的居民可以在Zebec.io上申请该卡,并计划于今年晚些时候在美国推出,美国候补名单已开放。
与 Mastercard 联合推出的 Zebec Card 正在让加密支付变得更加广泛。传统金融机构与加密生态的合作,意味着传统金融正在逐渐的与加密生态融入,Zebec 生态的扩张、ZBC通证应用场景的进一步广泛(包括销毁),正在成为ZBC通证上涨持续的利好消息。
除了面向欧洲地区的Zebec Card的推出外,$ZBC现在可以在 Coinbase Custody 上使用,这也是促进$ZBC通证上涨的利好之一。
该消息也正在被彭博社报道,并引发行业的广泛关注。

Poseiswap空投计划开启
据悉,Poseiswap 将拿出总量7%的通证为 Zepoch 节点持有者进行空投,而空投将总计分为三轮,Poseiswap 首期拿出总发行量1.4%(即总空投数量的20%) 对生态节点进行空投,具体规则如下:

1、其中25%给予早期生态节点(编号1-2317个节点)
这部分主要给予早期的 Zepoch 生态节点持有者,空投比例将按照持有节点数量空投,而空投解锁时间按照points折算到30-180天完成,节点需在空投前完成DEX交易交互与LP池质押交互操作,此外推荐人将获得额外空投收益。
2、其中75%针对新节点(包括未参与地平线计划获得APY奖励的节点),最高获得节点价值150%的APY空投。
这部分主要针对于新节点,
l 新购节点数量小于5个,将获得节点价值50%的空投
l 新购节点数量5至14个获得节点价值100%空投
l 新购节点数量大于等于15个节点获得节点价值150%空投
注意:可以获得什么级别的APY,看账户内所有节点数量,但是计算价值的时候,是看你新节点总金额。
这部分空投,将以24个月为解锁期,线性解锁,并且APY空投POSE通证的定价,将按照5日平局值计算,而推荐人将获得而外收益。
例:您同一个地址持有3个早期节点,2个新节点,那么怎么算得到多少价值的空投呢?
①、计算APY:3+2=5,所以可以拿100%的APY
②、计算价值:新节点是2个,所以您的空投价值就是这两个新节点购买花费的金额,假如这两个新节点总共5000U购买
空投价值即:5000U×100%=5000U
3、结算价格:$POSE数量将基于PoseiSwap推出后前五天的均价。
例如,如果您可得到的空投价值等于 10000 美元,而$POSE在推出的前五天的平均价值为 50 美分(0.50 美元),您将获得 20000 $POSE。
而针对早期参加过APY活动的节点,本次APY可按照比例累加,此规则仅针对本次活动。
Poseiswap 的空投更加定向,这意味着该空投并不像过往的空投那样,多数空投给“羊毛党”、“工作室”等,所以相对来说其空投更加具备精准性与定向性,以建立更深的价值基础。
此外,我们看到该空投定向且线性释放,这意味其并不会一次性大规模流向市场,而随着 Nautilus Chain 的布局,这些空投通证持有者也会逐渐的因其拥有空投的通证资产,而进一步获得交易的特权与权益,以进一步促进这些空投通证的刚需构建较为坚固的价格基础。
我们看到,Zebec 生态始终保持着较为迅猛的发展势头,并持续的对ZBC通证构建价值基本盘起到促进作用,而这些布局对于ZBC通证、Zebec生态的发展都是持续性的,目前也是布局 ZBC 的最佳时期。
