上传了网站源码怎么做过期网站查询
- 没有git的请先安装git。可以百度一下如何安装git。
- 建立文件夹工作文件夹我这里建立的是feikong文件夹。在feikong文件夹里下载源代码访问github

git clone https://github.com/OpenIPC/aviateur.git

3. 下载VS:VS下载地址
安装VS:选择如下两个模块进行安装

4. 安装openipc指引下载对应编译环境vcpkg。
注意下载下面内容前需要先安装vs的cmake编译环境。


全部安装完毕后显示上面的截图

CMake projects should use: "-DCMAKE_TOOLCHAIN_FILE=D:/feikong/vcpkg/scripts/buildsystems/vcpkg.cmake
添加环境变量



5. 使用如下命令下载3rd
git clone https://github.com/floppyhammer/revector.git
git clone https://github.com/metayeti/mINI.git
git clone https://github.com/nlohmann/json.git
git clone https://github.com/OpenIPC/devourer.git
git clone https://github.com/libsdl-org/SDL.git

下载完成后把这几个文件复制到 aviateur\3rd文件夹内覆盖复制。
6. 打开VS,使用github账号登录。然后打开aviateur目录
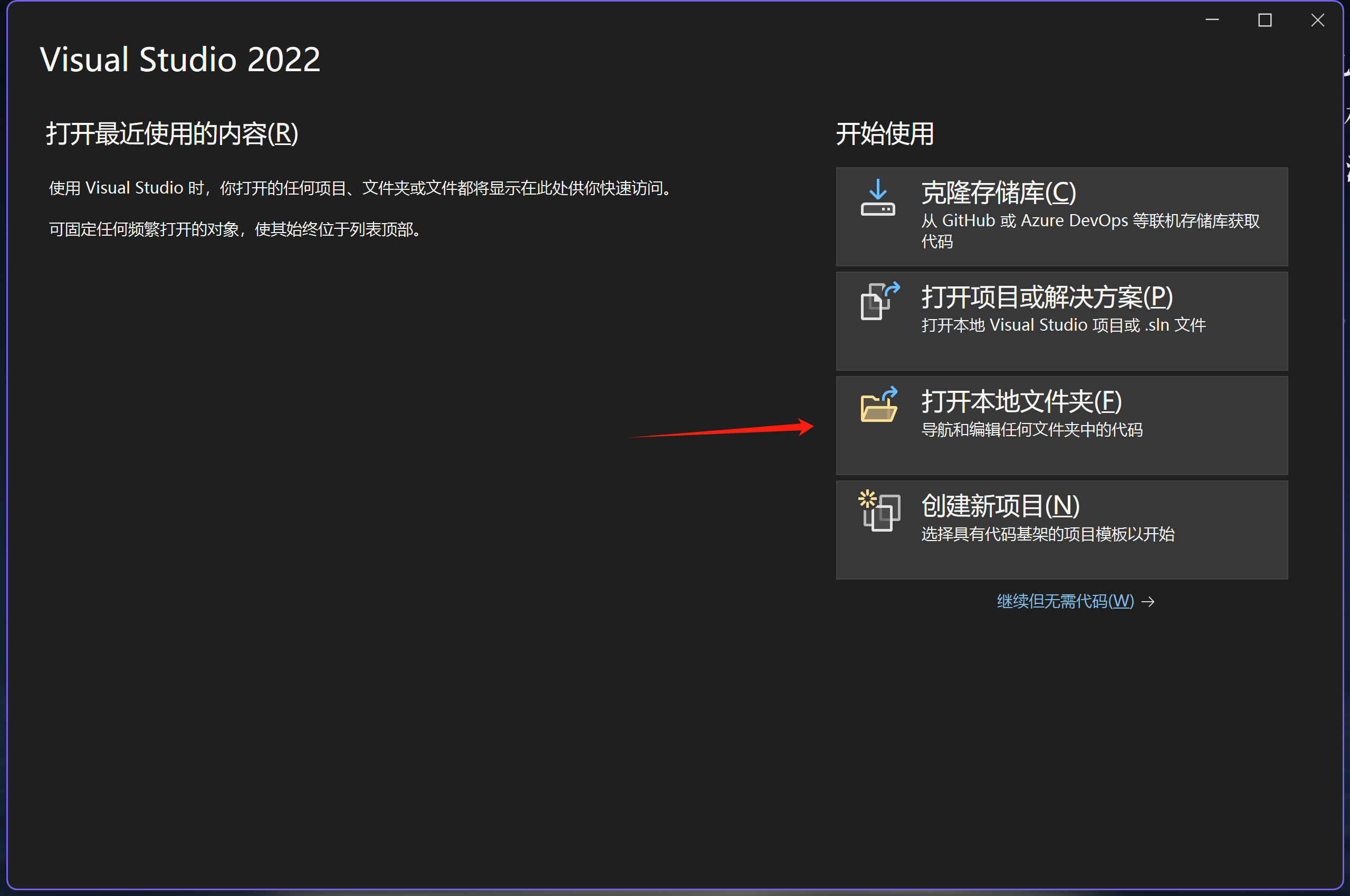
等待加载文件夹,加载完成后显示如下,打开src/main.cpp:

开始配置cmake

把下面两个变量配置成我们下载的vcpkg目录下的installed目录:D:\feikong\vcpkg\installed
保存后会在aviateur目录生成CMakeSettings.json文件用来调用正确的环境进行编译


然后就可以正常编译了。点击绿色空三角开始编译

编译成功后跳出如下运行界面。

编译的可执行.exe文件在如下目录:
D:\feikong\aviateur\out\build\x64-Debug\bin\assets
