当前位置：首页 > news >正文

网站html地图导航代码大全做ppt的网站叫什么

news 2025/11/3 5:24:45

网站html地图导航代码大全,做ppt的网站叫什么,广州商城网站制作网站,seo自动优化工具本文主要介绍算法中搜索算法的思想，主要包含BFS，DFS。搜索相关题目深度优先搜索和广度优先搜索广泛运用于树和图中，但是它们的应用远远不止如此。BFS广度优先搜索的搜索过程有点像一层一层地进行遍历，每层遍历都以上一层遍历的结果…

本文主要介绍算法中搜索算法的思想，主要包含BFS，DFS。

搜索相关题目

深度优先搜索和广度优先搜索广泛运用于树和图中，但是它们的应用远远不止如此。

BFS

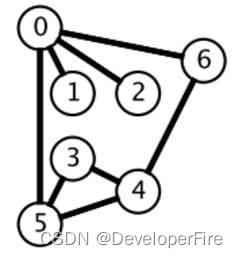
广度优先搜索的搜索过程有点像一层一层地进行遍历，每层遍历都以上一层遍历的结果作为起点，遍历一个距离能访问到的所有节点。需要注意的是，遍历过的节点不能再次被遍历。

第一层:

0 -> {6,2,1,5};

第二层:

6 ->

2 -> {}

1 -> {}

5 ->

第三层:

4 -> {}

3 -> {}

可以看到，每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离，推导出一个结论: 对于先遍历的节点 i 与后遍历的节点 j，有 di<=dj。利用这个结论，可以求解最短路径等最优解问题: 第一次遍历到目的节点，其所经过的路径为最短路径。应该注意的是，使用 BFS 只能求解无权图的最短路径。

在程序实现 BFS 时需要考虑以下问题:

队列: 用来存储每一轮遍历得到的节点；

标记: 对于遍历过的节点，应该将它标记，防止重复遍历。

计算在网格中从原点到特定点的最短路径长度

[[1,1,0,1],[1,0,1,0],[1,1,1,1],[1,0,1,1]]

1 表示可以经过某个位置，求解从 (0, 0) 位置到 (tr, tc) 位置的最短路径长度。

public int minPathLength(int[][] grids, int tr, int tc) {final int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};final int m = grids.length, n = grids[0].length;Queue<Pair<Integer, Integer>> queue = new LinkedList<>();queue.add(new Pair<>(0, 0));int pathLength = 0;while (!queue.isEmpty()) {int size = queue.size();pathLength++;while (size-- > 0) {Pair<Integer, Integer> cur = queue.poll();for (int[] d : direction) {int nr = cur.getKey() + d[0], nc = cur.getValue() + d[1];Pair<Integer, Integer> next = new Pair<>(nr, nc);if (next.getKey() < 0 || next.getValue() >= m|| next.getKey() < 0 || next.getValue() >= n) {continue;}grids[next.getKey()][next.getValue()] = 0; // 标记if (next.getKey() == tr && next.getValue() == tc) {return pathLength;}queue.add(next);}}}return -1;
}

组成整数的最小平方数数量

279. Perfect Squares (Medium)

For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.

可以将每个整数看成图中的一个节点，如果两个整数之差为一个平方数，那么这两个整数所在的节点就有一条边。

要求解最小的平方数数量，就是求解从节点 n 到节点 0 的最短路径。

本题也可以用动态规划求解，在之后动态规划部分中会再次出现。

public int numSquares(int n) {List<Integer> squares = generateSquares(n);Queue<Integer> queue = new LinkedList<>();boolean[] marked = new boolean[n + 1];queue.add(n);marked[n] = true;int level = 0;while (!queue.isEmpty()) {int size = queue.size();level++;while (size-- > 0) {int cur = queue.poll();for (int s : squares) {int next = cur - s;if (next < 0) {break;}if (next == 0) {return level;}if (marked[next]) {continue;}marked[next] = true;queue.add(cur - s);}}}return n;
}/*** 生成小于 n 的平方数序列* @return 1,4,9,...*/
private List<Integer> generateSquares(int n) {List<Integer> squares = new ArrayList<>();int square = 1;int diff = 3;while (square <= n) {squares.add(square);square += diff;diff += 2;}return squares;
}

最短单词路径

127. Word Ladder (Medium)

Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]Output: 5Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.

Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]Output: 0Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

找出一条从 beginWord 到 endWord 的最短路径，每次移动规定为改变一个字符，并且改变之后的字符串必须在 wordList 中。

public int ladderLength(String beginWord, String endWord, List<String> wordList) {wordList.add(beginWord);int N = wordList.size();int start = N - 1;int end = 0;while (end < N && !wordList.get(end).equals(endWord)) {end++;}if (end == N) {return 0;}List<Integer>[] graphic = buildGraphic(wordList);return getShortestPath(graphic, start, end);
}private List<Integer>[] buildGraphic(List<String> wordList) {int N = wordList.size();List<Integer>[] graphic = new List[N];for (int i = 0; i < N; i++) {graphic[i] = new ArrayList<>();for (int j = 0; j < N; j++) {if (isConnect(wordList.get(i), wordList.get(j))) {graphic[i].add(j);}}}return graphic;
}private boolean isConnect(String s1, String s2) {int diffCnt = 0;for (int i = 0; i < s1.length() && diffCnt <= 1; i++) {if (s1.charAt(i) != s2.charAt(i)) {diffCnt++;}}return diffCnt == 1;
}private int getShortestPath(List<Integer>[] graphic, int start, int end) {Queue<Integer> queue = new LinkedList<>();boolean[] marked = new boolean[graphic.length];queue.add(start);marked[start] = true;int path = 1;while (!queue.isEmpty()) {int size = queue.size();path++;while (size-- > 0) {int cur = queue.poll();for (int next : graphic[cur]) {if (next == end) {return path;}if (marked[next]) {continue;}marked[next] = true;queue.add(next);}}}return 0;
}

DFS

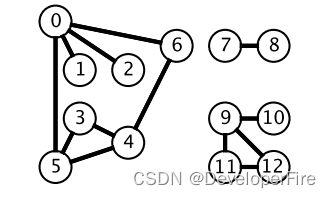
广度优先搜索一层一层遍历，每一层得到的所有新节点，要用队列存储起来以备下一层遍历的时候再遍历。

而深度优先搜索在得到一个新节点时立马对新节点进行遍历: 从节点 0 出发开始遍历，得到到新节点 6 时，立马对新节点 6 进行遍历，得到新节点 4；如此反复以这种方式遍历新节点，直到没有新节点了，此时返回。返回到根节点 0 的情况是，继续对根节点 0 进行遍历，得到新节点 2，然后继续以上步骤。

从一个节点出发，使用 DFS 对一个图进行遍历时，能够遍历到的节点都是从初始节点可达的，DFS 常用来求解这种可达性问题。

在程序实现 DFS 时需要考虑以下问题:

栈: 用栈来保存当前节点信息，当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。

标记: 和 BFS 一样同样需要对已经遍历过的节点进行标记。

查找最大的连通面积

695. Max Area of Island (Easy)

[[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int maxAreaOfIsland(int[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int maxArea = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {maxArea = Math.max(maxArea, dfs(grid, i, j));}}return maxArea;
}private int dfs(int[][] grid, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0) {return 0;}grid[r][c] = 0;int area = 1;for (int[] d : direction) {area += dfs(grid, r + d[0], c + d[1]);}return area;
}

矩阵中的连通分量数目

200. Number of Islands (Medium)

Input:
11000
11000
00100
00011Output: 3

可以将矩阵表示看成一张有向图。

private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int numIslands(char[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int islandsNum = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] != '0') {dfs(grid, i, j);islandsNum++;}}}return islandsNum;
}private void dfs(char[][] grid, int i, int j) {if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {return;}grid[i][j] = '0';for (int[] d : direction) {dfs(grid, i + d[0], j + d[1]);}
}

好友关系的连通分量数目

547. Friend Circles (Medium)

Input:
[[1,1,0],[1,1,0],[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.

好友关系可以看成是一个无向图，例如第 0 个人与第 1 个人是好友，那么 M[0][1] 和 M[1][0] 的值都为 1。

private int n;public int findCircleNum(int[][] M) {n = M.length;int circleNum = 0;boolean[] hasVisited = new boolean[n];for (int i = 0; i < n; i++) {if (!hasVisited[i]) {dfs(M, i, hasVisited);circleNum++;}}return circleNum;
}private void dfs(int[][] M, int i, boolean[] hasVisited) {hasVisited[i] = true;for (int k = 0; k < n; k++) {if (M[i][k] == 1 && !hasVisited[k]) {dfs(M, k, hasVisited);}}
}

填充封闭区域

130. Surrounded Regions (Medium)

For example,
X X X X
X O O X
X X O X
X O X XAfter running your function, the board should be:
X X X X
X X X X
X X X X
X O X X

使被 'X' 包围的 'O' 转换为 'X'。

先填充最外侧，剩下的就是里侧了。

private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
private int m, n;public void solve(char[][] board) {if (board == null || board.length == 0) {return;}m = board.length;n = board[0].length;for (int i = 0; i < m; i++) {dfs(board, i, 0);dfs(board, i, n - 1);}for (int i = 0; i < n; i++) {dfs(board, 0, i);dfs(board, m - 1, i);}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == 'T') {board[i][j] = 'O';} else if (board[i][j] == 'O') {board[i][j] = 'X';}}}
}private void dfs(char[][] board, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || board[r][c] != 'O') {return;}board[r][c] = 'T';for (int[] d : direction) {dfs(board, r + d[0], c + d[1]);}
}

能到达的太平洋和大西洋的区域

417. Pacific Atlantic Water Flow (Medium)

Given the following 5x5 matrix:Pacific ~   ~   ~   ~   ~~  1   2   2   3  (5) *~  3   2   3  (4) (4) *~  2   4  (5)  3   1  *~ (6) (7)  1   4   5  *~ (5)  1   1   2   4  **   *   *   *   * AtlanticReturn:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).

左边和上边是太平洋，右边和下边是大西洋，内部的数字代表海拔，海拔高的地方的水能够流到低的地方，求解水能够流到太平洋和大西洋的所有位置。

private int m, n;
private int[][] matrix;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public List<int[]> pacificAtlantic(int[][] matrix) {List<int[]> ret = new ArrayList<>();if (matrix == null || matrix.length == 0) {return ret;}m = matrix.length;n = matrix[0].length;this.matrix = matrix;boolean[][] canReachP = new boolean[m][n];boolean[][] canReachA = new boolean[m][n];for (int i = 0; i < m; i++) {dfs(i, 0, canReachP);dfs(i, n - 1, canReachA);}for (int i = 0; i < n; i++) {dfs(0, i, canReachP);dfs(m - 1, i, canReachA);}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (canReachP[i][j] && canReachA[i][j]) {ret.add(new int[]{i, j});}}}return ret;
}private void dfs(int r, int c, boolean[][] canReach) {if (canReach[r][c]) {return;}canReach[r][c] = true;for (int[] d : direction) {int nextR = d[0] + r;int nextC = d[1] + c;if (nextR < 0 || nextR >= m || nextC < 0 || nextC >= n|| matrix[r][c] > matrix[nextR][nextC]) {continue;}dfs(nextR, nextC, canReach);}
}

查看全文

http://www.yayakq.cn/news/991520/