做网站有哪些好公司建设网站聊天室
文章目录
- 新机器到了要做的事情
- 背景
- 检查机器
- 安装系统
- 装系统步骤
- 总结
新机器到了要做的事情
背景
@运维 一台机器到了,去看看机器情况,小编之前是开发呀,由于种种原因,阴差阳错的做了运维,本以为是应用运维,装装软件看看日志,理想很丰满、现实很骨感呀,好家伙,上来让我检查硬件,这下子慌了神,服务器那是听说过没见过呀。
想到了之前课本上的水手,那的思想就是临危不乱,稳住,不会咱去查资料呗,这时候又想起了飞哥,开工干活。
可以看得出这是在小公司,大公司也不会让非专业的人士来做专业性很强的工作,在这里说好听点可以说是运维工程师,说的难听点那是在帮开发打杂。
检查机器
首先要看的是
- 服务器的电源指示灯、风扇和硬盘指示灯等是否正常工作
- 检查是否有任何物理损坏,例如松动的电线、损坏的散热器等
- 连接显示器,查看自检是否正常
- 查看系统内的硬盘、CPU、内存情况
机器检查结束后对机器进行入网操作
- 服务器都有管理口和业务口,首先对两个IP进行设置
- 安装操作系统,当系统安装完成后才能正常的使用
安装系统
- 设置BIOS,在设置BIOS的时候要选择UEFI的方式启动
- 使用U盘进行安装,一般是F10、F2以及Del键盘快速或者进入设置启动
- 安装Centos 7.9的步骤如下,步骤不是很完整,但重要的都在
如果不使用UEFI的方式启动,则无法使用4T以上的磁盘,UEFI的方式只认GPT分区的磁盘,或者没有格式的磁盘,MBR的则不支持UEFI,MBR支持legacy模式启动
装系统步骤
选择第一个直接安装,第二个是测试安装源的包,然后安装
- 选择语言英语即可
- 总体安装步骤如下

- 对磁盘分区,我习惯选择LVM分区,我觉得好管理,有大佬说大厂不用LVM,因为LVM影响性能的
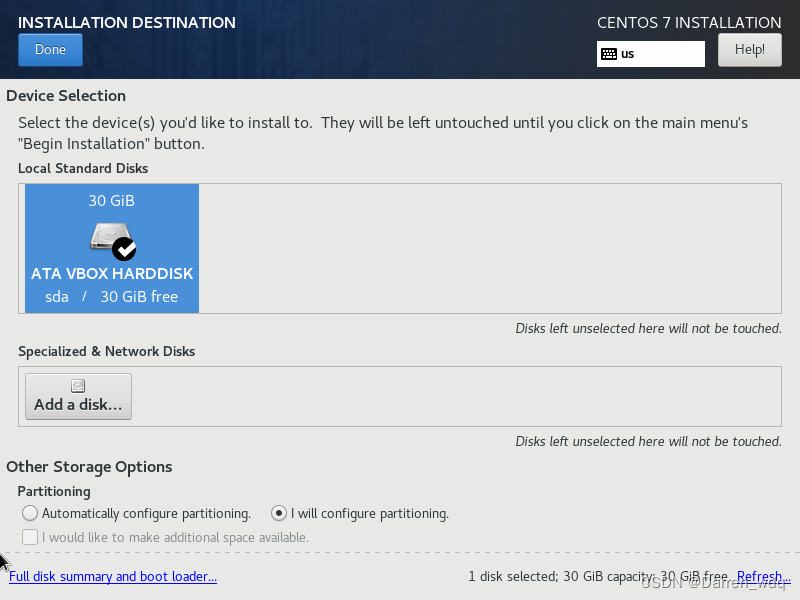
- 建议分三个区
/boot 1024M
swap 16G
/ 剩余的空间,可以不填写
关于swap分区有人这么说的
4G以内的物理内存,SWAP 设置为内存的2倍,不超过4G。
4-8G的物理内存,SWAP 等于内存大小。
8-64G 的物理内存,SWAP 设置为8G。
64-256G物理内存,SWAP 设置为16G。
当内存达到一定量时,是使用SWAP分区,当SWAP分区也不够时,那Linux就会杀掉占用内存最多进程,如盖值为60时,则内存超过100-60=40%的时候,使用SWAP分区,当使用SWAP分区时,程序会很慢。
# 查看超过多少%时使用SWAP分区
cat /proc/sys/vm/swappiness
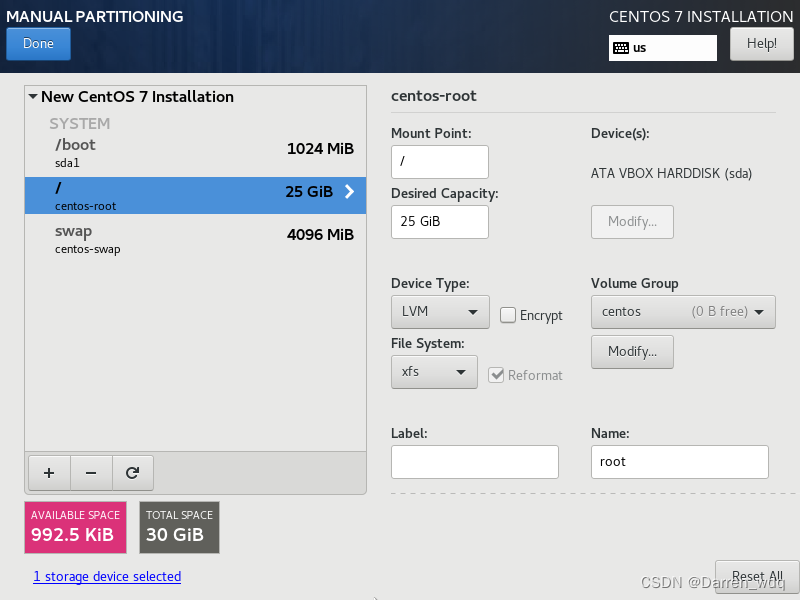
-
切勿反抗接受就好
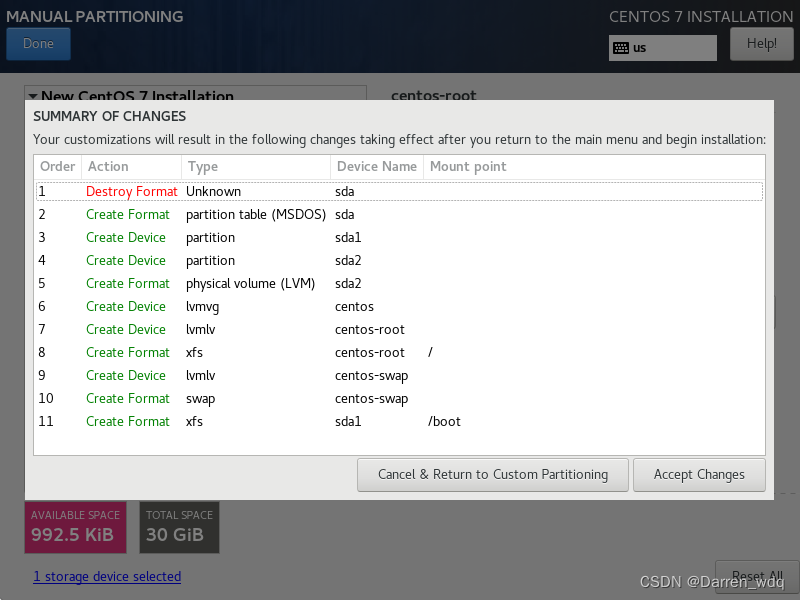
-
设置网络和主机名
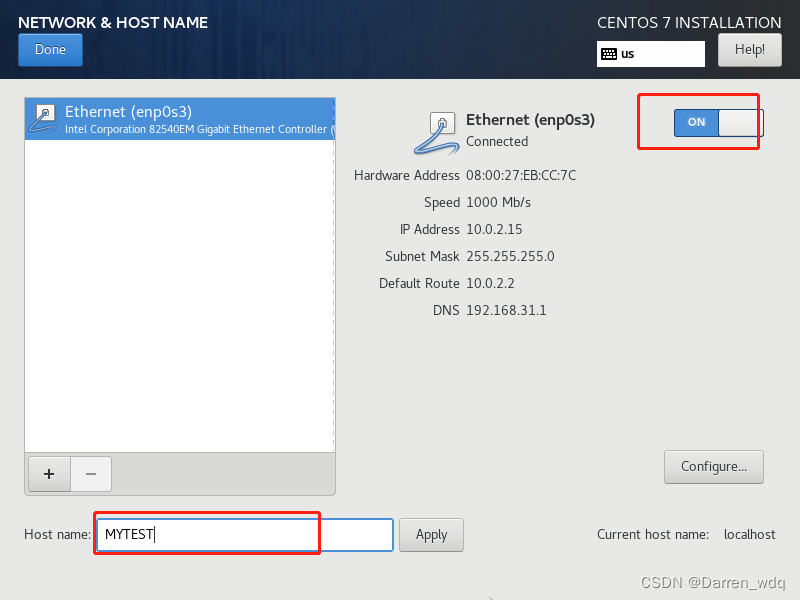
宿主机中开启这个,客户机关闭这个即可,关掉后会节省一些内存,当系统崩溃时记录日志的
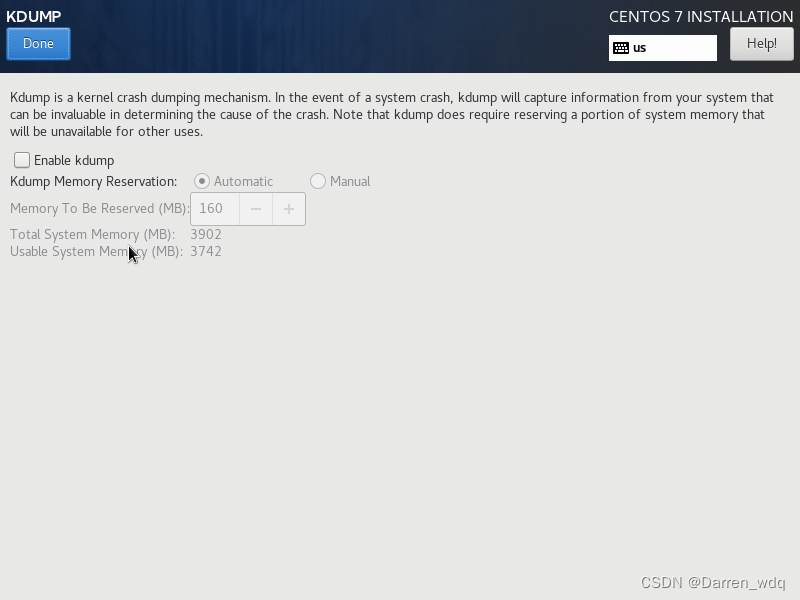
-
这时候再去设置时间,选择亚洲/上海,先打开网络再进行时区设置可以同步时间,这样会少安装一个软件包
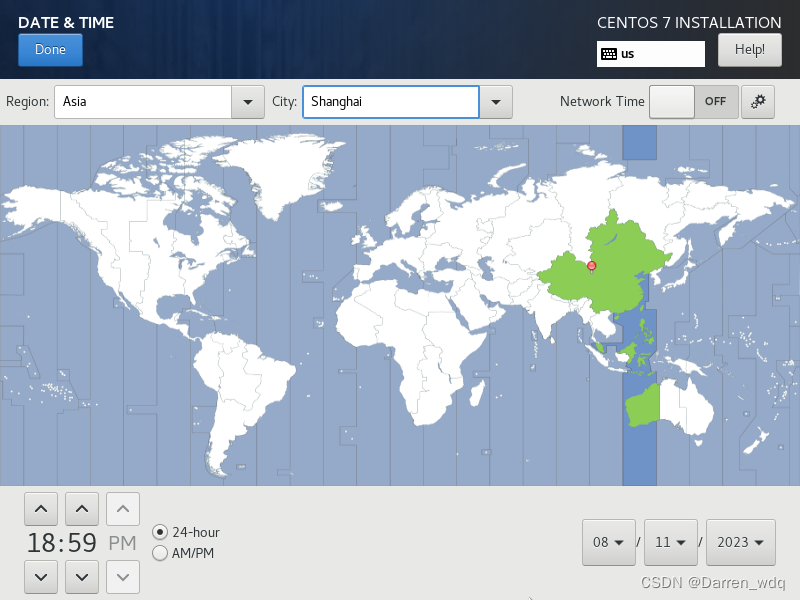
-
服务器的话建议选择最小安装
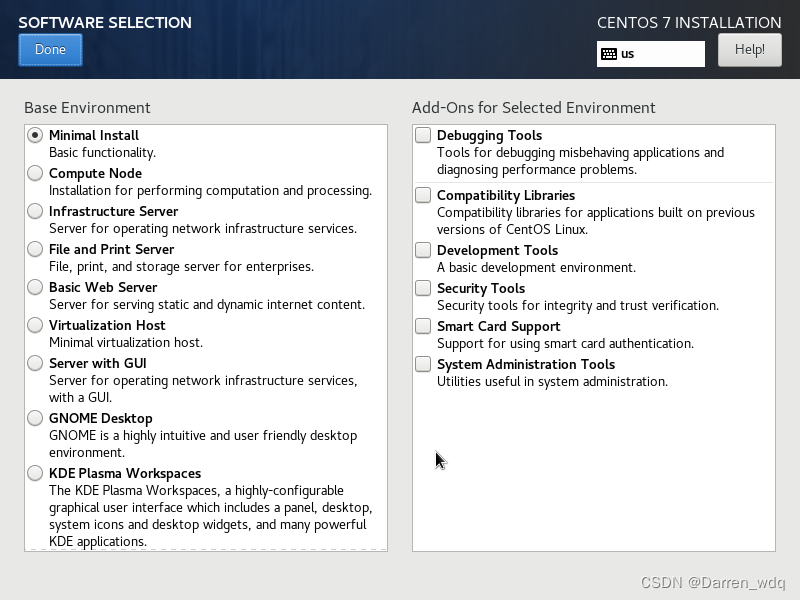
-
都设置好后,开始安装
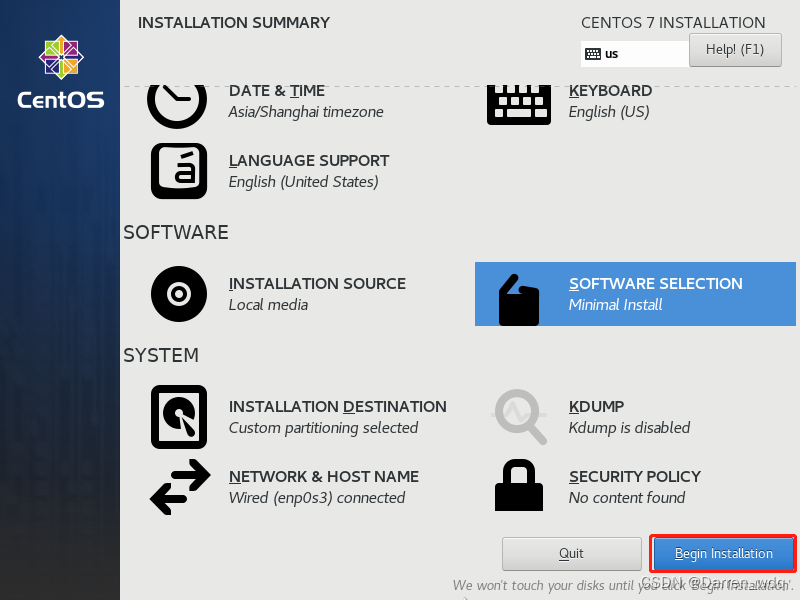
设置root密码
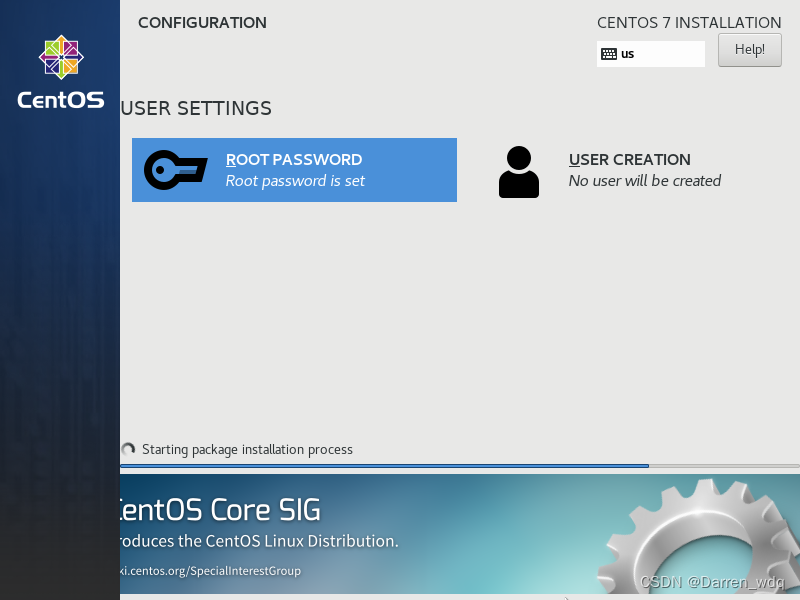
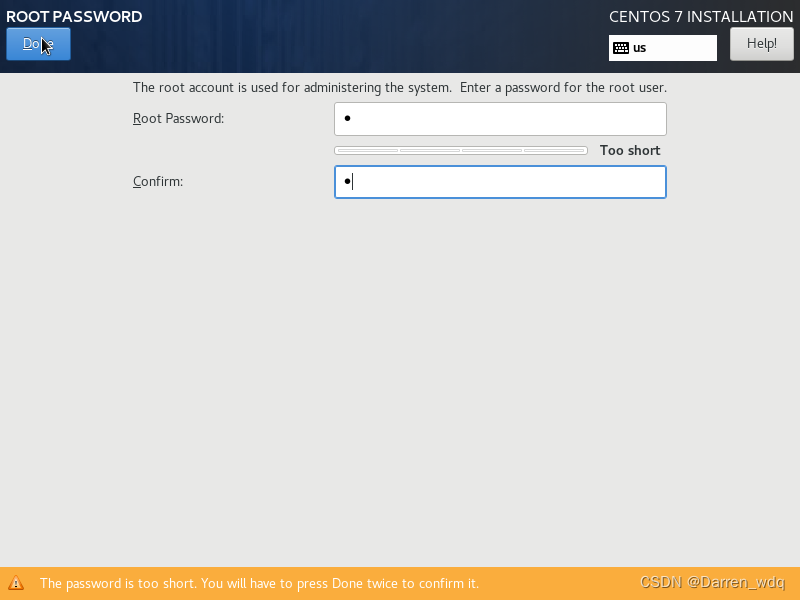
可以创建用户也可以不创建用户
- 接下来等待安装即可,最后重启即可
总结
这个机器是要做宿主机的,里面要装好几台虚拟机,找了一圈,最终选用KVM,其实现在装虚拟机都很多种如
- KVM
- VirtualBox
- VMware vSphere/ESXi
- Proxmox
- Microsoft Hyper-V
这些虚拟机软件感觉VirtualBox和Hyper-V都是在个人机器上用的居多,ESXi也不熟悉,就选用了KVM,现在好多都不用KVM了,而是选择OpenStack、ZStack,这些不仅支持集群,而且性能较好,因为这里只有一台机器,有很多不确定性,先选择了KVM,下一篇我们介绍安装KVM。
