网站首页怎么做全屏swf东莞手机建网站
文章目录
- 前言
- 一、类的理解
- 二、如何创建ABAP类
- `a.`类的定义与构成
- `b.`类的访问区域
- `c.`特殊方法
- `d.`类的继承
- 三、类中参数的使用
- `a.`IMPORTING / EXPORTING
- `b.`CHANGING
- `c.`RETURNING
- `d.`EXCEPTION
- 四、使用类做一个小案例
- `a.`CLA_PER 计算周长
- `b.`CLA_AREA 计算面积
- `c.`EXCEPTION 的应用
- 五、抽象类
- `a.`抽象类的定义
- `b.`抽象方法的使用
- `c.`抽象类的作用 与 好处优点
- 六、最终类
- `a.`最终类定义
- `b.`最终方法定义
- 七 、接口 (INTERFACE)
- `a.`接口的定义
- `b.`接口的使用
- `c.`接口的作用 与 好处优点
- 八、事件
- `a.`触发类定义
- `b.`捕获类定义
- `c.`运行展示
- `d.`值得注意的点
- `e.`注册所有可以触发该事件的实例
- `f.`静态事件
- 九、总结
前言
这篇文章给大家介绍一下SAP中ABAP面向对象,在ABAP最初的时候只有面向过程的编写方式,所谓面向过程就是我在编写过程中是有一个很明显的因果关系的,就是我因为我要怎么样才要做什么 我从哪里到哪里,从一个开端到一个结尾不断去进行的,在后来ABAP是引入了面向对象的概念,也就是Object-oriented简称OO,面向对象它的核心其实是一种解决方案,它是把我们生活中具体的的事务进行一个抽象化,在抽象的过程中呢我们抓住两个核心的内容,分别是属性和方法,属性是用来描述我们这个对象具体的属性以及特征的,方法它是用来定义对象有哪些具体行为的。面向对象的实现过程核心就是类,类就是我们对具体的事务进行抽象创建的东西就叫做类,类相比我们原本的那种代码编写方式有一些优点,例如代码的重复利用,对数据进行封装使用。类有三大特性:封装、集成、多态。这些特性文章后面都会讲解到。
一、类的理解
对于类的理解大家可以去网上搜着看,因为这是一种思想有人会将它讲的很好。这里我也结合自己的理解大概介绍一下我个人的理解。首先 万物皆对象 万物皆可类,世间的一切东西一切事务都可以抽象成类。就拿 狗 来说,狗有很多品种 有各种各样的。我们可以把狗抽象成为一个类,然后就可以创造出无数个对象,创造的这些对象可以说都是独一无二的,那么如何去设计 狗 这个类,这个是我们要思考设计的,首先类有属性,就是特征,狗有什么特征呢?狗有颜色 花色, 狗有大型小型中型,狗有 公 有母,狗的性格 有温顺 有凶狠 ,狗的体力 有强 有弱。。。等等 等等 这些都是属性 都是特征。在用类创建一个狗的对象的时候这些属性特征我们都可以用参数传递表示。类还有方法,对于狗这个类来说 ,狗可以叫,可以跑,可以睡觉,可以吃饭。。。。等等 等等 这些都是狗的行为和方法。对象在执行了这些方法之后具体会做什么 那么就是在这个方法里面去设定了,对于狗来说 吃饭了体型可以长胖 睡觉了可以增加体力。这就是一个狗类大致的设计,这就是面向对象思想。如果没有面向对象 我们想想 如果在程序或者游戏中要创建1000个狗 得如何去设计数据结构 得写多少个变量,这是不敢想想的。会非常臃肿与复杂 并且程序可维护性太低了。得乱死。当我们用面向对象这种思想去设计创建1000个狗的时候 那么代码的复用 和 可维护性是很高的。编写代码的效率也是很高的 要创建一个狗的对象 只需要 一行代码即可。而且狗的这些属性状态都会被保存在对象里面,用起来 访问起来也是很方便的。说到访问 类 也有 公共 保护 私有 这些个访问修饰符,可以控制对类变量资源的访问权限。这也是我们一般数据类型难以达到的。再用游戏举例 吃鸡中 有各种各样的车,小轿车 皮卡车 装甲车 ,游戏中的车也肯定是需要被抽象成为类的,对于 属性 有 耐久度,有颜色,有速度,有油量。方法的话 可以开动跑起来,可以爆炸,可以爆胎。当子弹打到车的话 就会触发耐久度-1的方法。当耐久度为0的时候 车就会执行爆炸的方法。所以说万物皆对象 万物皆可类。类有三大特性 封装 继承 多态,封装 就是代码可以复用 创建一个对象只需要传参就像 调用方法直接用对象调用就行。继承 让我来理解就是对创建的类再次进行了细分,比如我可以创建一个 车的类,然后越野车这个类可以继承 车的类,小轿车这个类也可以继承车这个类,商务车这个类也可以继承车这个类。那么这些 越野车 小轿车 商务车 其实都有自己不同的属性特性。可以在这些继承的类中设置不同的特性 比如设置 大小 载人量 商务车肯定是大于小轿车的。这就是继承吧。多态的话 字面意思理解就是多种型态就是对象表现出来的多种型态,比如我们创建了一个动物类 ,动物类都是会有叫声的。然后 我们的狗类 和 猫类 都继承这个动物类,然后创建 一个狗对象 和 猫对象,这两个对象都去调用叫的这个方法,那么会表现出来不同的型态,狗会 汪汪汪 而 猫会 喵喵喵,这就是当我们调用同样的方法 可能因为对象的不同而表现出不同的型态。也就是多态允许不同的对象对相同的方法作出不同的响应。多态一般都是继承来实现的 当我们子类去调用方法的时候可以根据自己当前的属性特征来重写父类的方法,这意味着,尽管调用的是相同的方法,但根据对象的实际类型特征属性等,可以执行不同的代码。多态性提高了代码的灵活性和可扩展性。
二、如何创建ABAP类
在SAP中类有全局类和本地类,全局类就是我们SE24创建的类,全局类是在任何程序任何函数中都可以使用的,本地类就是我们在程序中创建的类,本地类只能在本程序中使用。下面我主要介绍本地类的创建使用。
a.类的定义与构成
本地类声明类的时候我们会分成两个部分去定义,分别是 1、 构成类的一些具体的组件项目 2、 类方法具体的内容。
1.类的定义
类就如下图所示定义,详情还请还代码中注释。DEFINITION 就是我们上面所说的第一部分, IMPLEMENTATION 是第二部分。
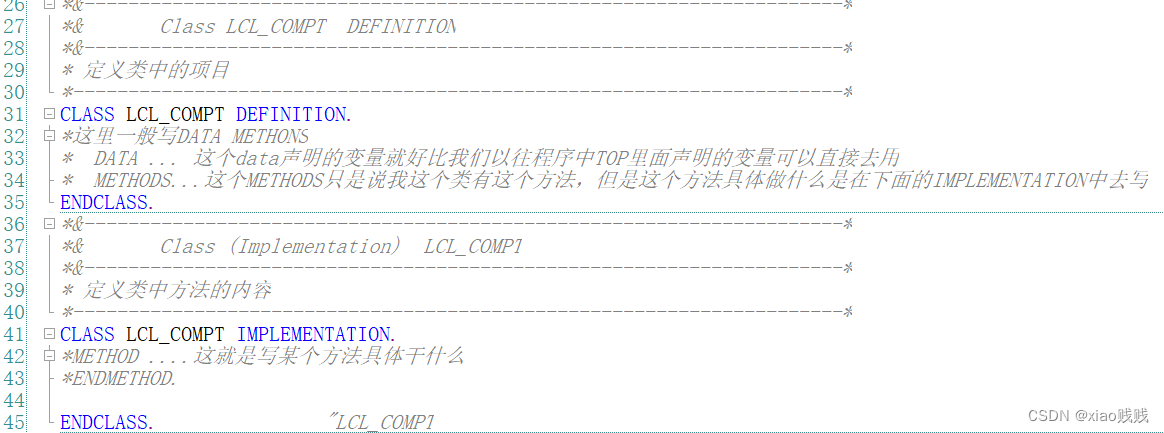
2.类的构成要素
类的所有要素都要在声明部分实现也就是写在DEFINITION中,一共有大三要素 1.属性(Attributes): 属性其实就有点类似于变量常量可以用DATA / CONSTANTS来定义。 2.方法(Method): 方法就是我具体实现的一些功能,例如我传进去两个参数这个方法就帮我计算这个两个参数的和。就是封装起来的一些小功能。方法可以直接去使用也可以定义一些交互参数去使用。 3.事件(Event): 它其实是一中特殊的方法,定义之后可以由两个类关联使用的,例如我这边达到某种状态了我触发一个事件在另外一个类中我们可以针对这个事件去进行处理,后面会详细讲到的。
3.实例组件 静态组件 常量
类中的 属性 和 方法 都分为两种 分别为: 静态属性(CLASS-DATA 、 CLASS-CONSTANTS),静态方法(CLASS-METHODS),实例属性(DATA),实例方法(METHODS)。 如下图所示 类方法、类属性 顾名思义就是类的方法和属性可以直接用类去调用不用创建对象,实例方法、实例属性 就是需要实例化一个对象 必须通过对象才能调用。在类中声明的常量用类和对象都可以去访问。但是一般是通过类用 => 去访问。

b.类的访问区域
1.访问区域如何定义
类在DEFINITION定义的过程 有一个分区的概念,就是我类中所定义的属性 方法 这些组件都必须定义在某个区域中。如下面的案例所示。
a.给组件设定访问区域

b.使用类的实例属性实例方法
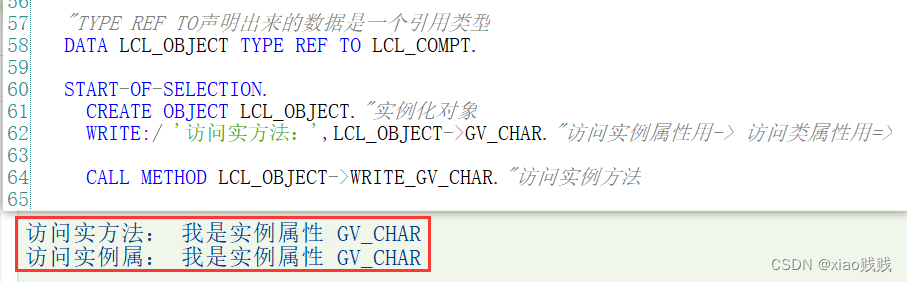
c.使用类的静态属性静态方法
实例组件是依附于实例的,不同的实例之间有自己不同的属性值都是相互独立的,静态组件大家用的都是一套存在类里面的。就是不管任意哪个实例去调用静态组件效果都是相同的值。下面我们对之前定义的类增加了一个静态属性和静态方法,然后让之前的实例方法中访问了我们定义的静态属性,接着我们使用=>访问了静态属性静态方法。
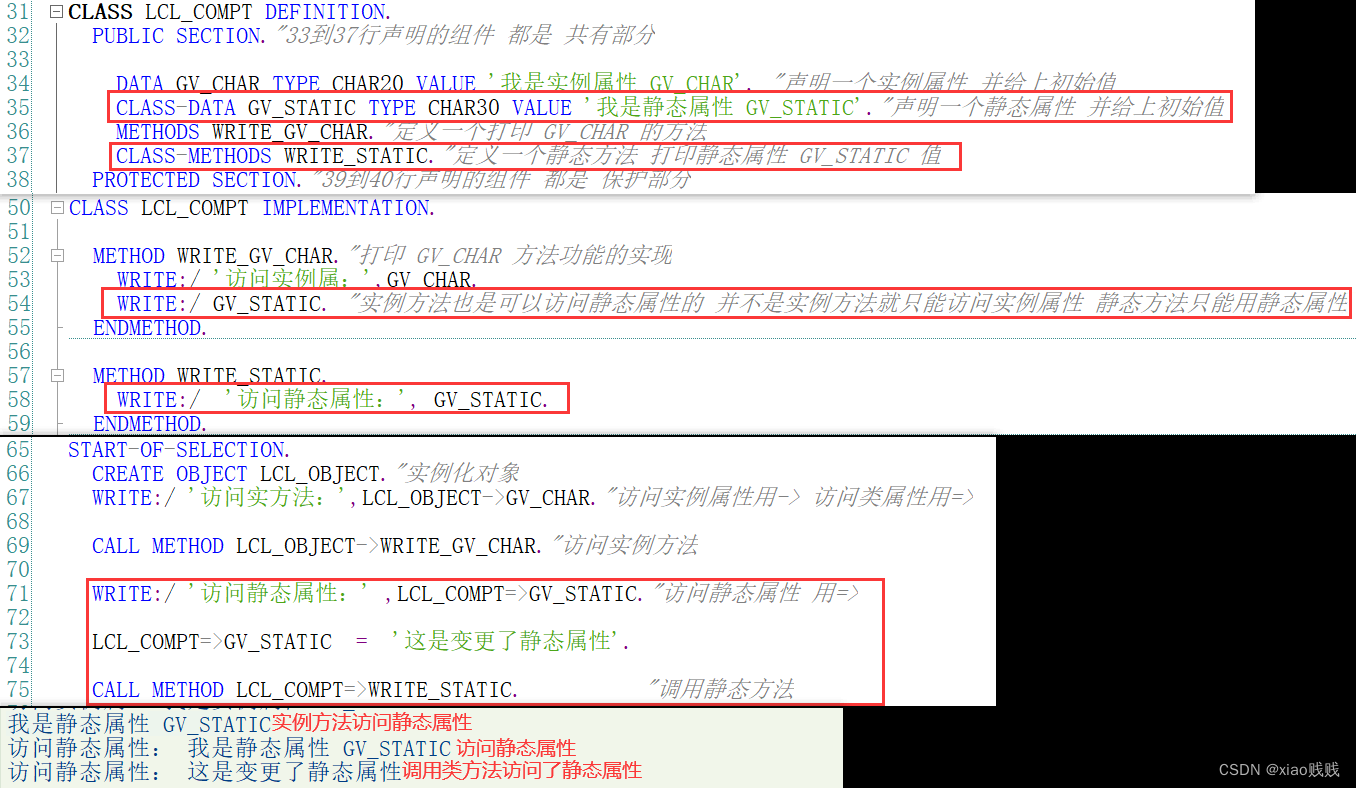
在 DEFINITION 中声明的组件不管是属性还是方法 它是属于什么样的可见性什么级别的,一共分为三个访问区域,分别是 1.公有部分(Public Section)、2.保护部分(Protected Section) 、3.私有部分(Priivate Section) 要弄清这三个访问区域有什么区别 我们要了解到类中的这些变量方法 谁都可以去用。首先比如我们有一个类它有一个Data ,一般情况这个Data 1、类本身可以去用 2、继承类可以用 3、还有外部可以去用。 类本身去用就是我当前 DEFINITION 里面声明的这些东西我自己可不可以用,继承类去用 就是我参照这个类再声明了一个类跟这个类是有关联的我能不能去用,外部去用 就比如我创建了一个报表程序 然后我调用这个类 或者是这个类已经使用结束了我在其他地方再去使用能不能用。如果访问区域是 私有部分(Priivate Section) 的话 也就是只有在我类的内部我自己本身可以用,你不能在其他程序代码中去访问调用。下面有一个表格大家可以看一下。
| . | 公有部分 PUBLIC | 保护部分 PROTECT | 私有部分 PRIVATE |
|---|---|---|---|
| 这个类的方法 (类本身) | √ | √ | √ |
| 类继承的方法 (继承类) | √ | √ | X |
| 对外的数据接口 (外 部) | √ | X | X |
2.访问区域的实际应用案例
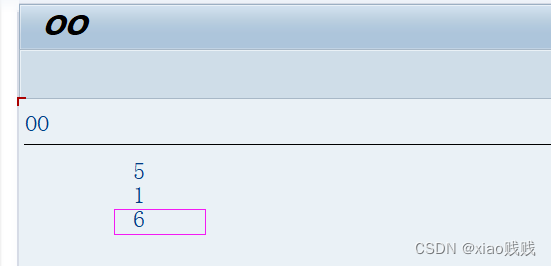
下面这个例子中我们在类中定义的属性和方法都是实例属性 实例方法,上面我们说过 实例属性 和 实例方法一定要通过 对象 去访问,不能通过 类 直接访问。还有一点就是我们定义的实例组件这些属性 方法 都是存储在每个对象之中的 相互独立互不影响的。比如一个狗类 有一个体力值的实例属性初始值都为10,当我创建两个 狗对象 的时候 这两个 狗对象 的体力值都为10,当我修改了 狗对象1 的体力值为15的时候,并不会影响我们狗对象2的体力值。 就是实例属性依附于某个对象 ,静态属性依附于类。 下面这个例子大家详细看注释就行。
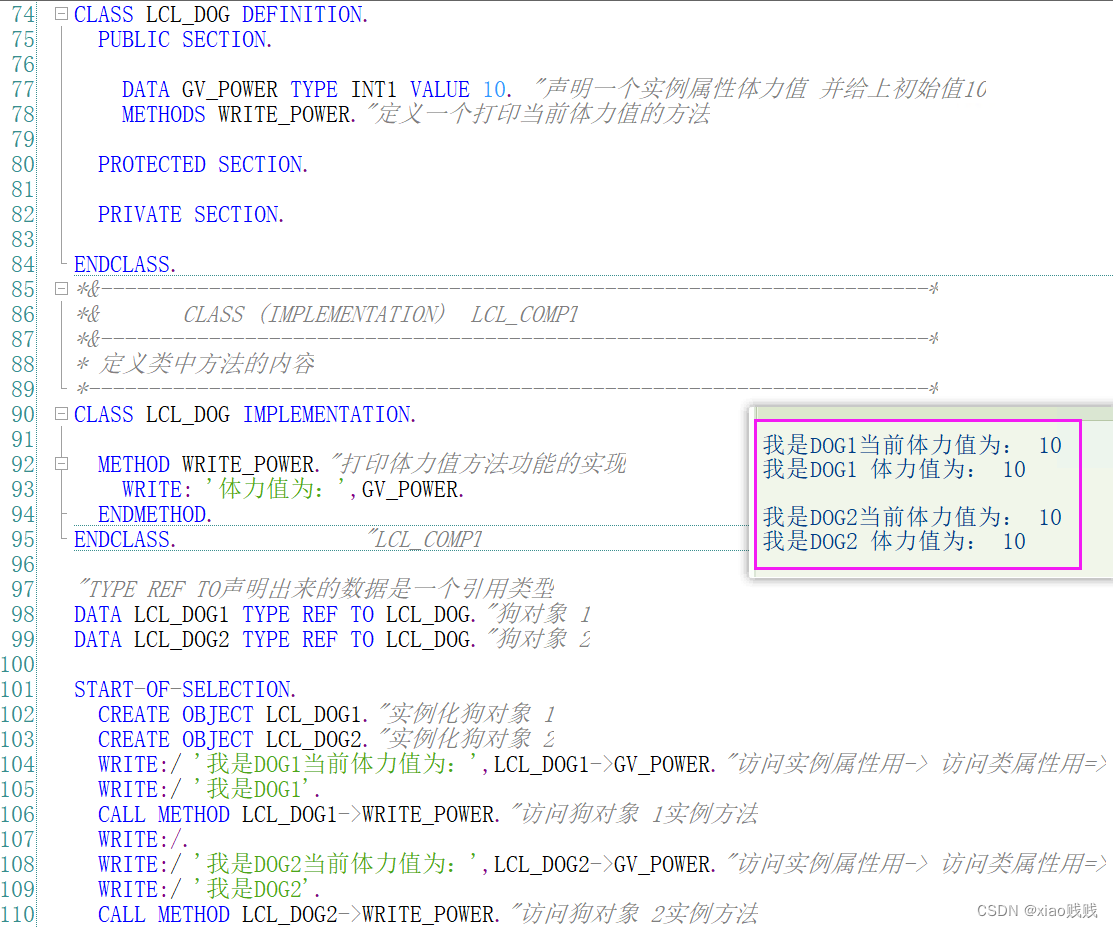
上面的注释和运行结果很详细,现在我去单独修改 狗对象1 的体力值 再查看运行结果,可以看到 狗对象2 的体力值并没有受影响。

a.组件定义在公共部分的效果
其实上面打印狗对象体力值的案例就是定义在公共部分访问调用的效果,这里就不再演示了。
b.组件定义在保护部分的效果
下面我们将实例属性和实例方法都定义在了保护区,当激活的时候发现会报错不允许我们访问受保护的属性方法。这是因为我们在这个类的外部访问或者修改了这个类的实例属性实例方法。也是就是说我要访问和调用保护区的属性方法我只能在类的内部区访问。
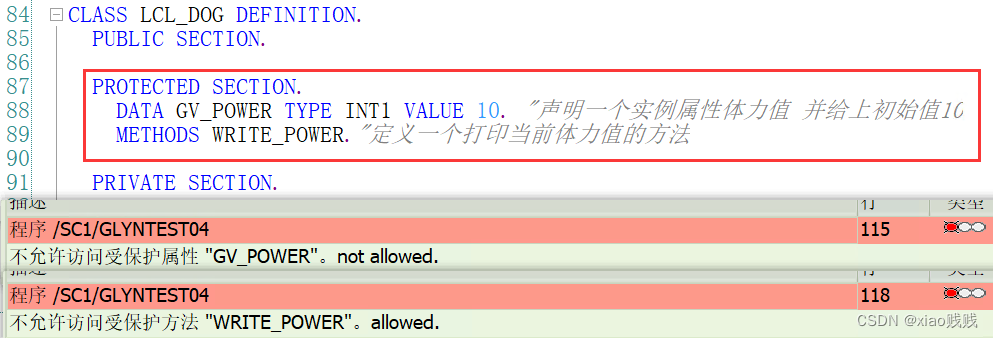
下面这个例子就很明显的能看出效果,当我们把方法定义在公共部分,把属性定义在保护部分。然后这个方法在外部是可以调用的,然后这个方法又在类的内部去访问了实例属性,这就是只能在我类的内部我类本身可以去访问使用,你不能在类的外面去访问调用。
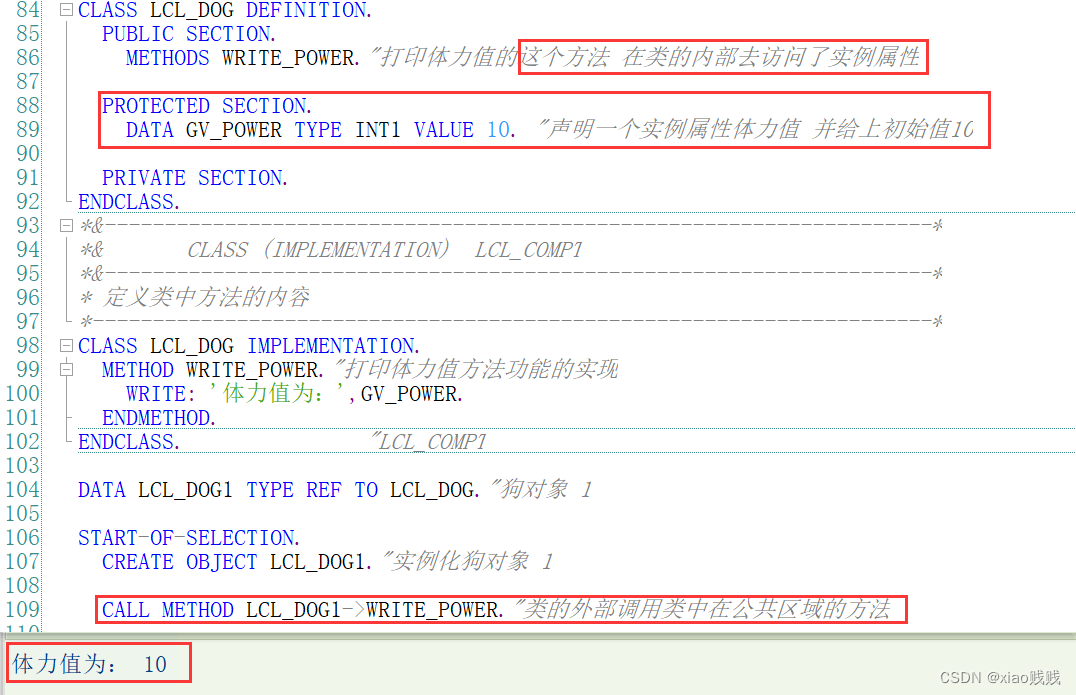
c.组件定义在私有部分的效果
通过上面的案例我相信大家已经理解了访问区域有什么作用,如果定义在私有部分就是只能我类内部我类本身去访问调用。和保护部分的区别就是 保护部分的组件 继承类也可以去访问。私有部分请看如下案例。
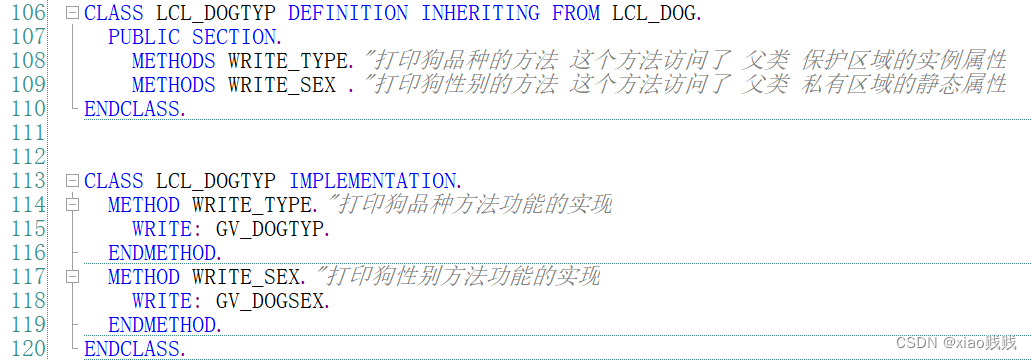
1.首先我们在类中的保护区域 定义了一个狗品种的实例属性,再到私有区域定义了一个狗性别的静态属性。

2.我们再定义一个继承类,继承类其实就不用从0开始定义组件,因为它把父类的一些东西都带了过来,父类的定义就必须从0开始定义一些组件。我们这里定义一个 狗品种的类 并用关键字 INHERITING FROM 继承 狗类 也就是它的父类了。然后这个 狗品种 类我们定义了两个方法 分别去访问了父类中 保护区域 的实例属性 和 私有区域 的实例属性。
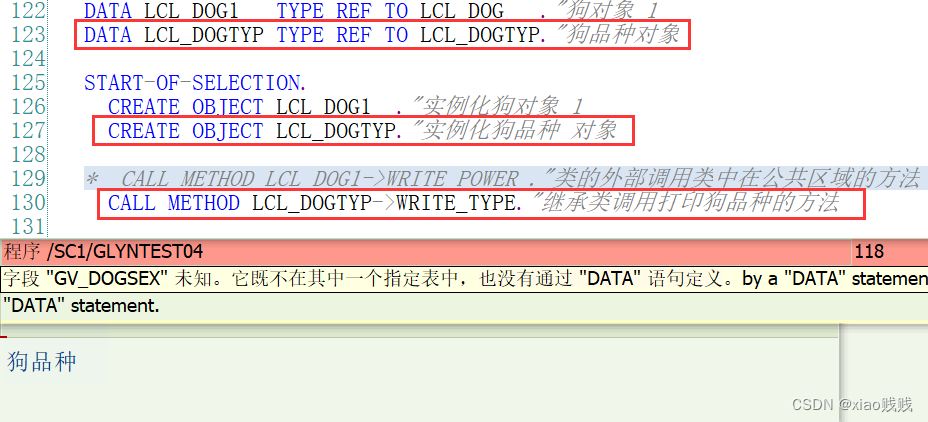
3.现在的结果很明显,就是我们不能访问 父类中私有区域 的静态属性,但是可以访问保护区域的实例属性。并且如果访问私有区域的属性会直接报错不存在 并不是报错不允许访问。
c.特殊方法
在类中有一种特殊的方法叫构造方法,这个方法是在对象进行实例化的时候自动进行初始化调用,如果没有构造方法的话,这个对象实例化之后一定是一个空的,就是对象没有什么属性值,当我想在对象初始化的时候想给某些特征赋值的时候,那么这个时候就要使用构造方法,构造方法是没有返回值的,只能进行数据的传入。构造方法不能显式的去调用。一般都是在CREATE OBJ 实例化对象的时候进行调用传参,一个类只能有一个 构造方法 和一个 类构造方法,这两种方法的区别是,类构造方法是实例化第一个对象的时候进行自动调用,而 构造方法是每次实例化对象的时候都会自动调用。
其实个人感觉构造方法就是为了灵活的创建不同属性的对象,其实在上面的例子中我们有一些实例属性用 VALUE 关键字设定了默认了属性值,每次实例化对象的时候都是固定的值了不能灵活变动,当然我们可以再进行修改属性值以达到我们想到的对象属性状态。
但是有了构造方法就不一样了,我们每次可以传入不同的值,而且这个方法是自动调用的,比如我们想要创建两个狗对象,狗对象1 要求是 黄色 性别为 母 狗,狗对象2 要求是 白色 性别为 公 狗,这样我们在 CREATE 实例化对象的时候就可以给构造方法直接传入不同的属性值来达到我们这两个对象不同的属性状态。
1.类构造方法的使用
类构造方法是通过 CLASS-METHODS CLASS_CONSTRUCTOR 来进行声明的,方法名是固定的。
a.定义类构造方法
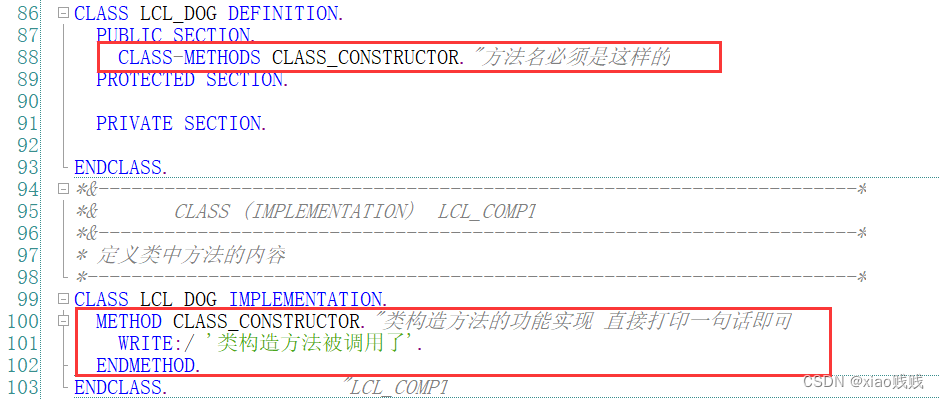
b.类构造方法的初始化调用
可以看到我们只是实例化了两个对象并没有去调用方法,但是类构造方法确实是被调用了,这就是初始化调用,并且 类构造方法只会在第一个对象实例化的时候调用一次后续实例化对象都不会再调用了。
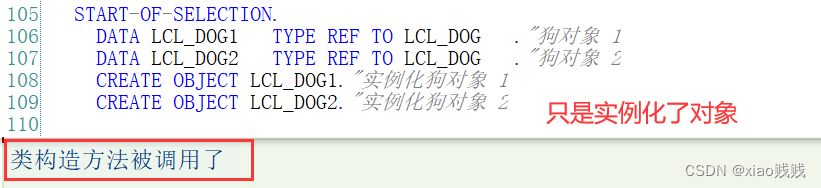
2.构造方法的使用
构造方法是通过 METHODS CONSTRUCTOR 来进行声明的,同样的方法名也是固定的。
a.定义构造方法
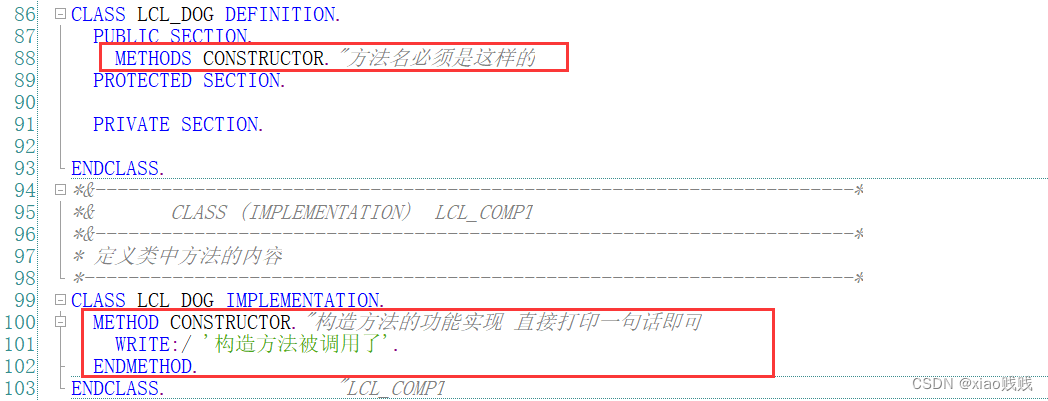
b.构造方法的初始化调用
下面的构造方法被调用了两次是因为我们实例化了两个对象,这两次构造方法的调用意义是不一样的,它是为了不同的对象而调用服务的。
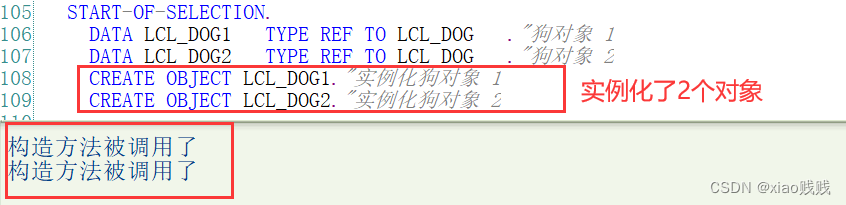
3.应用构造方法到案例中
我们可以设想我们在做一款游戏,这个游戏中有一个生存的人类,人类有一个属性值为孤独状态还有一个属性值为幸福度,游戏中还有可爱的小狗狗,当有狗狗存在的时候,人类的孤独状态就变为 不孤独。当游戏中出现3个不同颜色的狗狗时幸福度就叠满。
这个案例我在做的时候我发现了一个值得注意的问题。就是 类构造方法并不是我们想的那样是实例化第一个对象的时候就会执行一次。而是只要你 访问类的静态属性、调用类的静态方法,或者 实例化类的对象,类构造方法就会被调用。
a.代码示例

b.运行效果
我只是访问了静态属性并没有实例化对象类构造方法也被 调用了 num 从0变为了1
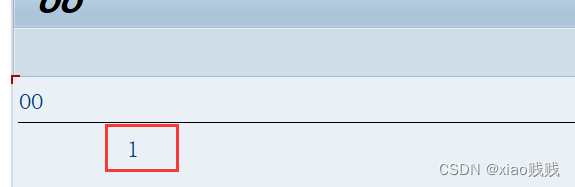
c.所以记住这句话
访问类的静态属性、调用类的静态方法、实例化类的对象,类构造方法就会被调用。且后续不会再被调用也就是只会执行一次。
d.类的继承
类的继承我们在上面做继承类访问父类私有区域的案例中也介绍过如何定义继承类,下面我们再介绍一下继承类其他的特点和使用方法。
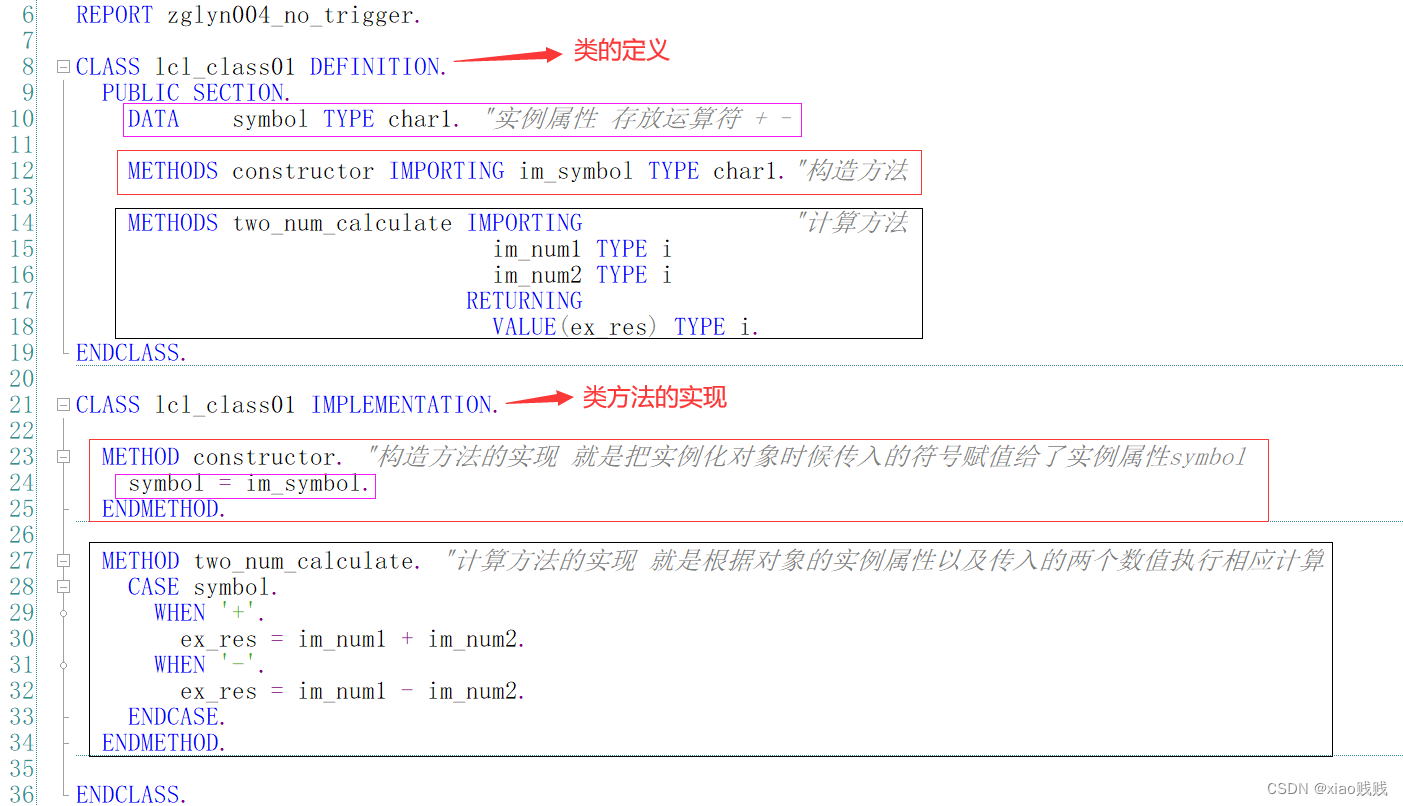
我们还是用一个案例来进行讲解吧,我们定义一个两数计算的类,这个类有构造方法,在实例化对象之前必须传入 加号 或者 减号,如果传入 加号 那么这个对象就是用来计算加法的,如果传入减号 那么这个对象就是用来计算减法的,类中有一个计算方法,给这个方法传入两个数值就能返回相应的计算结果。这个类就用做是我们的 父类。
再定义一个子类,继承我们上面的父类,这个子类有一个方法可以对父类计算的方法做调整,这里我们调整成为计算传入两个数值的乘法。
1.定义使用父类
定义父类主要运用 构造方法、实例属性、实例方法 以及 实例方法发参数的传入传出。参数这块的使用不明确的可以先看 本文: 三、类中参数的使用
a.定义
详情还请看代码中的注释
b.使用
详情还请看代码中的注释

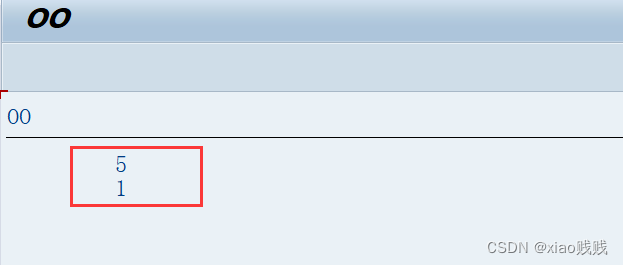
c.运行效果
传入的数值都是一样的,但是第一个对象是加法 3+2=5,第二个对象是减法 3-2=1
d.复制代码
复制代码在后面
2.定义使用继承类
主要看下图中的文字标注和代码中的注释即可。
a.定义
这里的定义我们主要演示对父类方法的重写。下面还有对父类方法的重载。
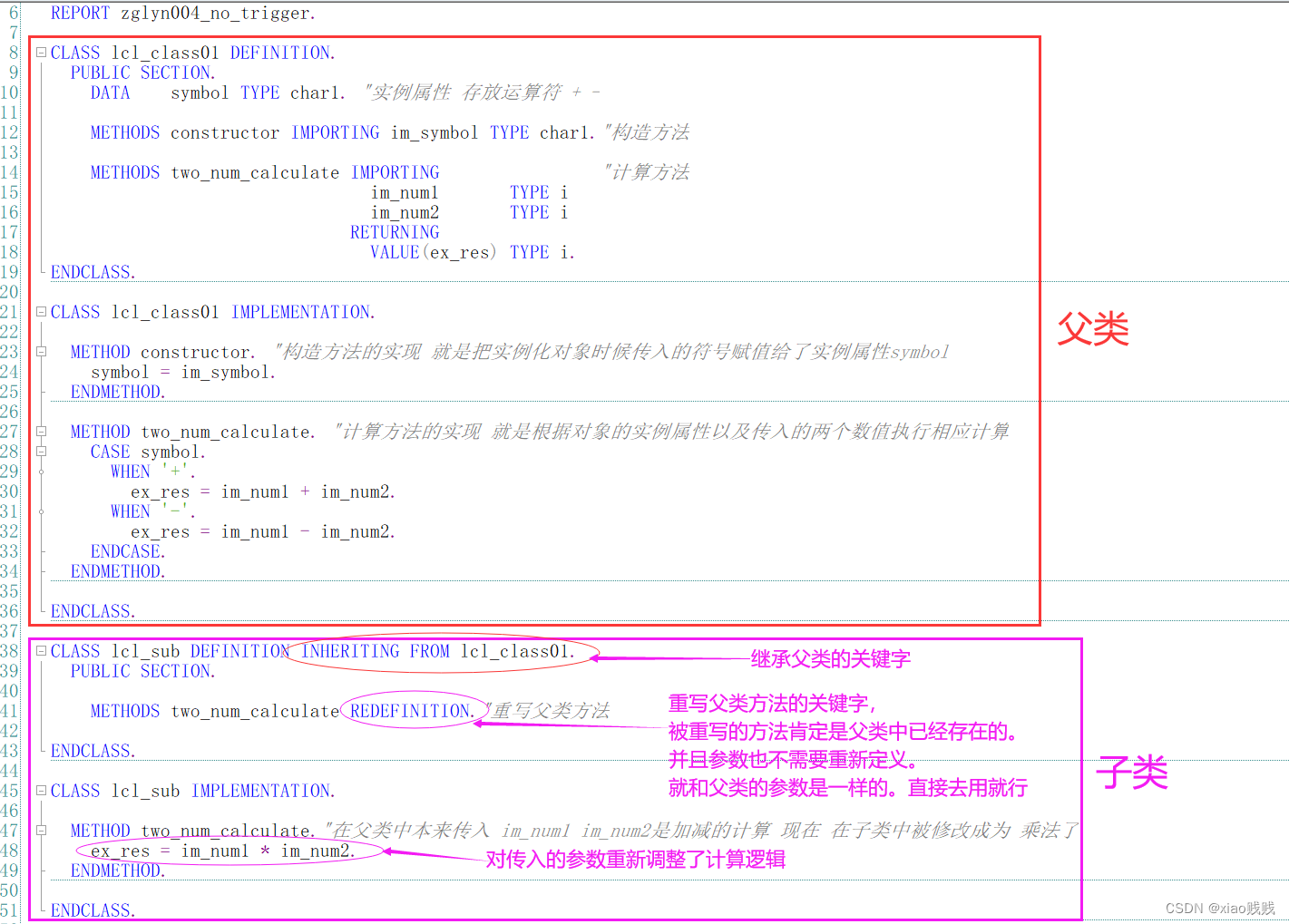
b.使用重写方法
详情还请看下图中文字的标注和代码中的注释,这里需要注意的是尽管我们子类中没写构造方法但是父类有我们就必须传参。尽管这个参数我们可能目前用不上。
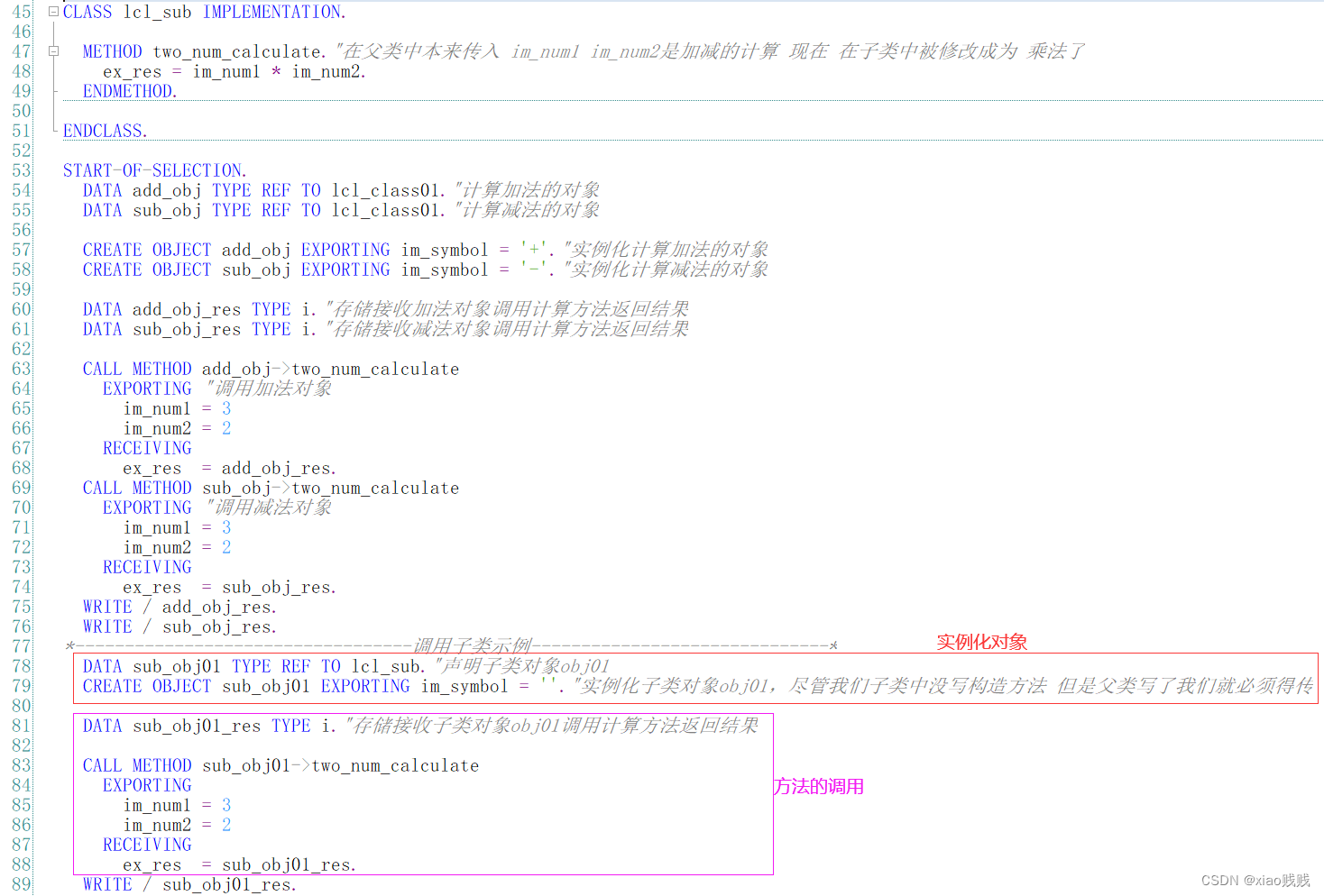
2 * 3 = 6
c.重载父类方法
这里我还是用一个案例来进行演示。现在有这么一个需求我在子类中定义一个方法,这个方法可以调用我父类加减计算的方法也可以调用我子类乘法计算的方法。那么此时就出问题了。two_num_calculate 这个方法在我父类中是计算加减的,在子类中之后被我修改成为计算乘法的了。现在 我子类中另外一个方法想同时调用这两个方法是不是感觉就冲突了?我们如何实现这样的效果呢?新定义的这个方法可以调用我父类加减计算的方法也可以调用我子类乘法计算的方法。这个问题具体看下图,要解决这个问题我们需要使用重载父类方法。
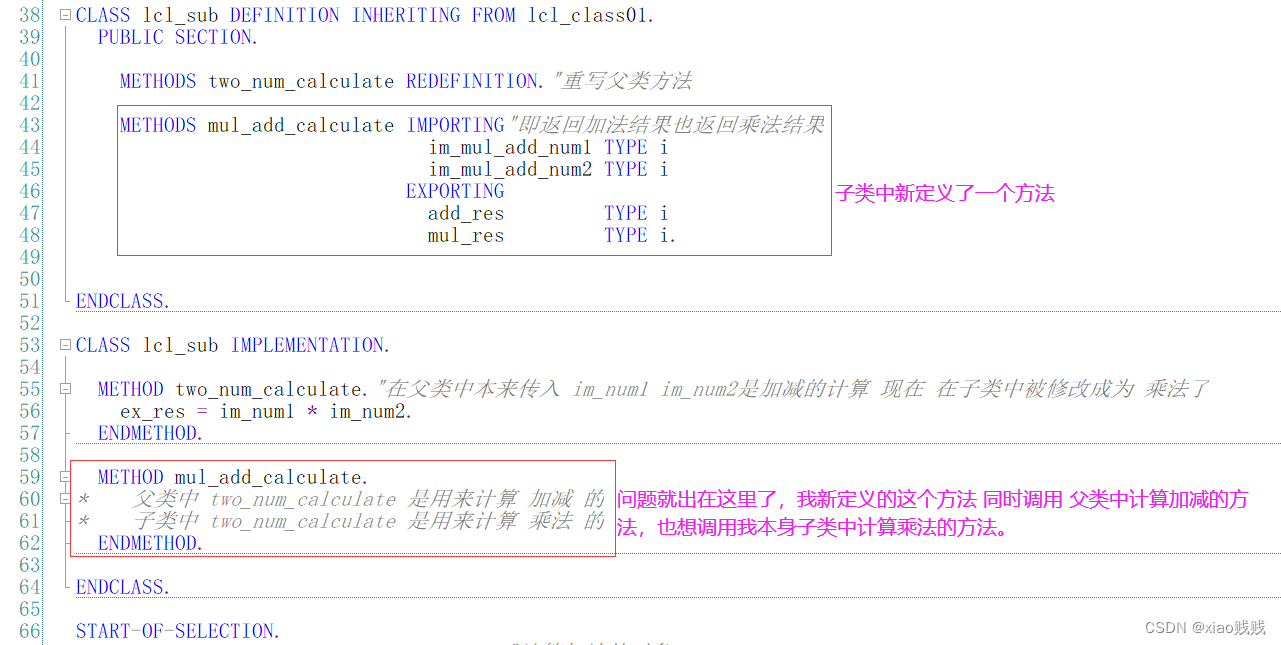
1.首先声明一点
我们并不会实现上面说的那样的效果,就是新定义了一个方法 我会在原来方法重写中调整修改达到同样的效果 主要是演示这个方法重载。上面只是为了让大家更好的理解这种情况。
2.使用SUPER关键字方法重载
详情请看代码中的注释和图片的文字标注。SUPER 关键字只能在 使用了 REDEFINITION 关键字的方法中调用原来父类的方法名。
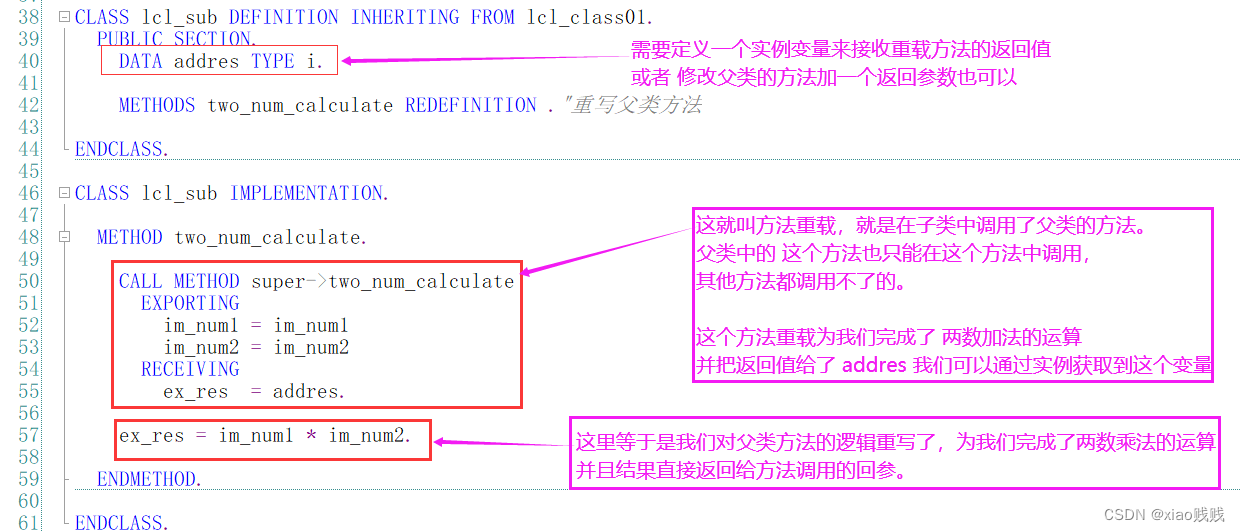
3.调用即结果展示

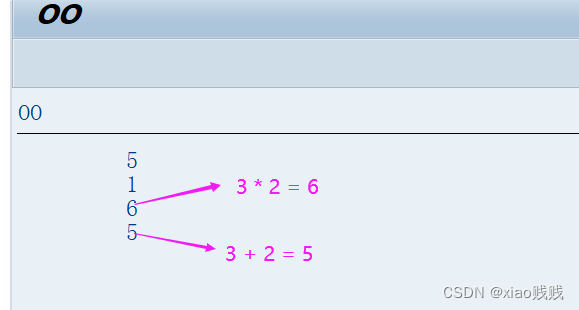
4.其他注意事项
上面我们说的是使用SUPER调用了父类的方法,如果我们想在类中调用自己本身的方法 直接调用即可 就跟我们正常调用方法一样。也可以写在方法名前面写个me->。详情请看下图注解。
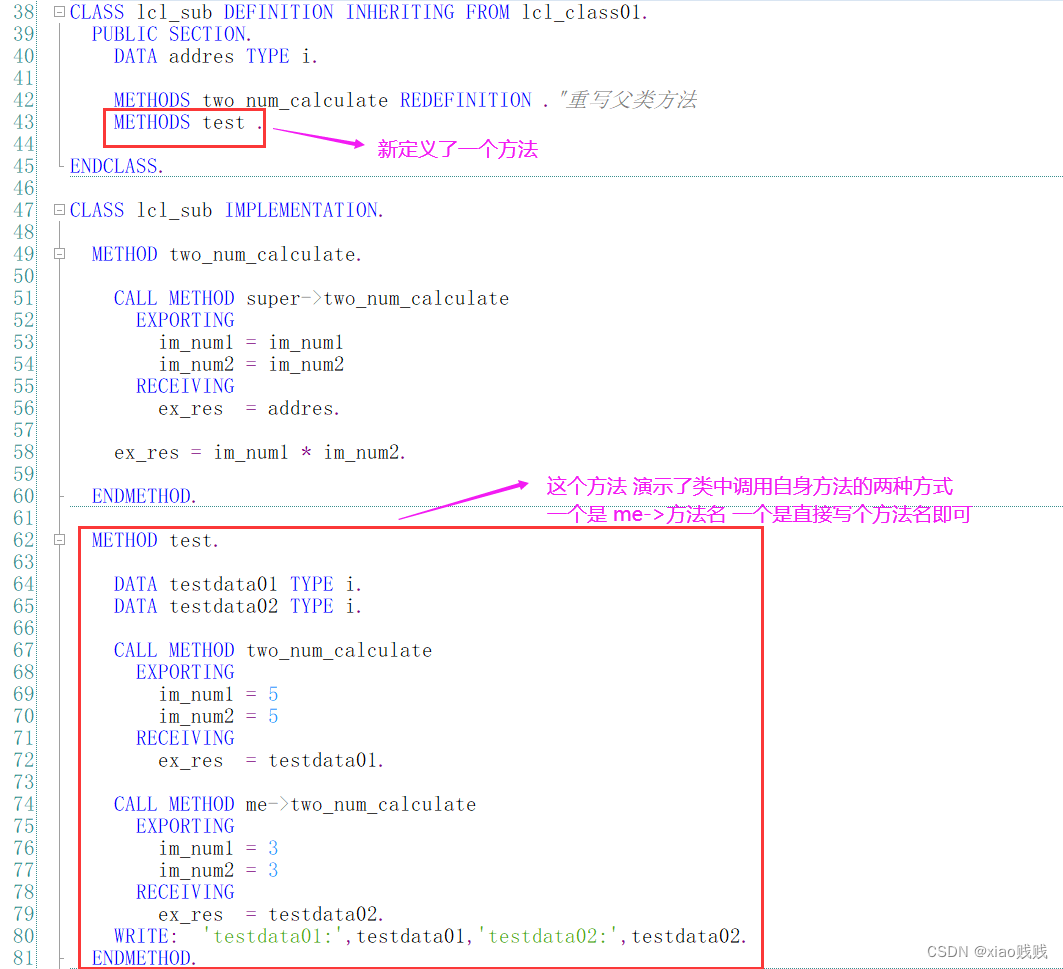

5 * 5 = 25 、3 * 3 = 9

3.Copy 代码
REPORT zglyn004_no_trigger.CLASS lcl_class01 DEFINITION.PUBLIC SECTION.DATA symbol TYPE char1. "实例属性 存放运算符 + -METHODS constructor IMPORTING im_symbol TYPE char1."构造方法METHODS two_num_calculate IMPORTING "计算方法im_num1 TYPE iim_num2 TYPE iRETURNINGVALUE(ex_res) TYPE i.
ENDCLASS.CLASS lcl_class01 IMPLEMENTATION.METHOD constructor. "构造方法的实现 就是把实例化对象时候传入的符号赋值给了实例属性symbolsymbol = im_symbol.ENDMETHOD.METHOD two_num_calculate. "计算方法的实现 就是根据对象的实例属性以及传入的两个数值执行相应计算CASE symbol.WHEN '+'.ex_res = im_num1 + im_num2.WHEN '-'.ex_res = im_num1 - im_num2.ENDCASE.ENDMETHOD.ENDCLASS.CLASS lcl_sub DEFINITION INHERITING FROM lcl_class01.PUBLIC SECTION.DATA addres TYPE i.METHODS two_num_calculate REDEFINITION ."重写父类方法METHODS test .ENDCLASS.CLASS lcl_sub IMPLEMENTATION.METHOD two_num_calculate.CALL METHOD super->two_num_calculateEXPORTINGim_num1 = im_num1im_num2 = im_num2RECEIVINGex_res = addres.ex_res = im_num1 * im_num2.ENDMETHOD.METHOD test.DATA testdata01 TYPE i.DATA testdata02 TYPE i.CALL METHOD two_num_calculateEXPORTINGim_num1 = 5im_num2 = 5RECEIVINGex_res = testdata01.CALL METHOD me->two_num_calculateEXPORTINGim_num1 = 3im_num2 = 3RECEIVINGex_res = testdata02.WRITE: 'testdata01:',testdata01,'testdata02:',testdata02.ENDMETHOD.ENDCLASS.START-OF-SELECTION.DATA add_obj TYPE REF TO lcl_class01."计算加法的对象DATA sub_obj TYPE REF TO lcl_class01."计算减法的对象CREATE OBJECT add_obj EXPORTING im_symbol = '+'."实例化计算加法的对象CREATE OBJECT sub_obj EXPORTING im_symbol = '-'."实例化计算减法的对象DATA add_obj_res TYPE i."存储接收加法对象调用计算方法返回结果DATA sub_obj_res TYPE i."存储接收减法对象调用计算方法返回结果CALL METHOD add_obj->two_num_calculateEXPORTING "调用加法对象im_num1 = 3im_num2 = 2RECEIVINGex_res = add_obj_res.CALL METHOD sub_obj->two_num_calculateEXPORTING "调用减法对象im_num1 = 3im_num2 = 2RECEIVINGex_res = sub_obj_res.WRITE / add_obj_res.WRITE / sub_obj_res.
*----------------------------------调用子类示例------------------------------*DATA sub_obj01 TYPE REF TO lcl_sub."声明子类对象obj01CREATE OBJECT sub_obj01 EXPORTING im_symbol = '+'.DATA sub_obj01res TYPE i.CALL METHOD sub_obj01->two_num_calculateEXPORTINGim_num1 = 3im_num2 = 2RECEIVINGex_res = sub_obj01res.WRITE / sub_obj01res.WRITE / sub_obj01->addres.WRITE / .CALL METHOD sub_obj01->test.
三、类中参数的使用
类函数可以拥有多个输入输出参数,类的输入输出接口参数必须与类函数中所定义类型保持一致。
a.IMPORTING / EXPORTING
数据输入/输出接口,接口参数可以参考单个变量,结构,或者内表。
1.IMPORTING
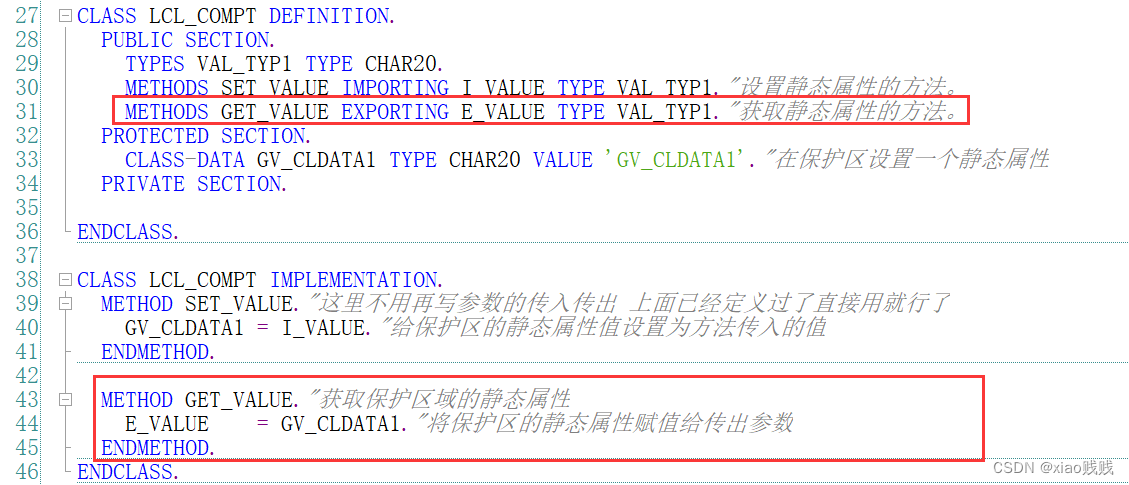
我们定义 一个SET_VALUE的方法,来给我们类中的静态属性设置值的一个方法,给这个方法设置一个传入参数。
注意在实现方法功能的时候 不用再写参数的传入传出 上面已经定义过了直接用就行了。
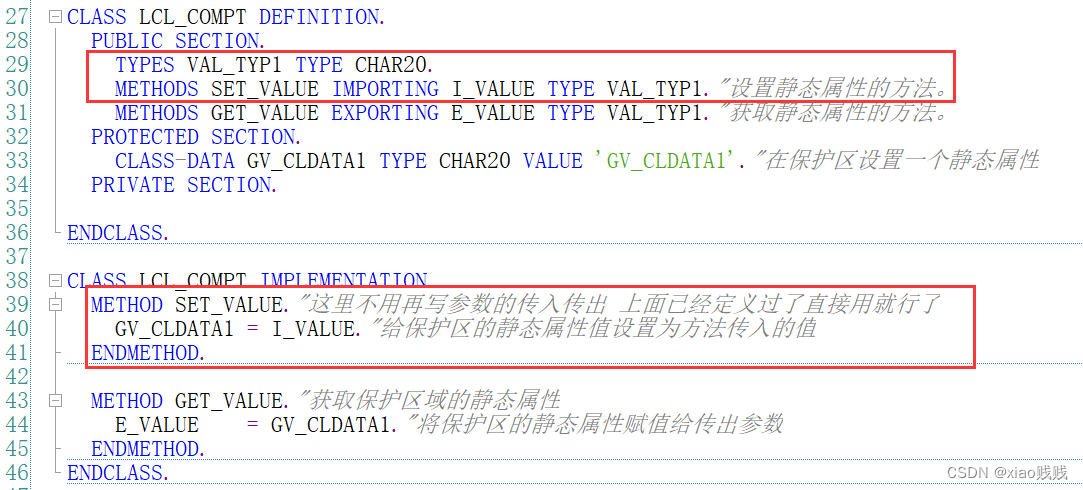
2.EXPORTING我们定义 一个GET_VALUE的方法,来获取我们类中的静态属性值的一个方法,给这个方法设置一个传出参数。
3.调用定义方法
下面我们来使用这两个方法 SET_VALUE 和 GE_VALUE。
方法中要 IMPORTING 传入的参数 我们在调用方法的时候要使用 EXPORTING 来将参数传入。方法中要 EXPORTING 传出的参数我们在调用的时候要用 IMPORTING 去接收方法中传出的参数,还有就是要注意传入传出的参数一定要跟方法里面的类型相兼容。 调用过程详情请看注释。
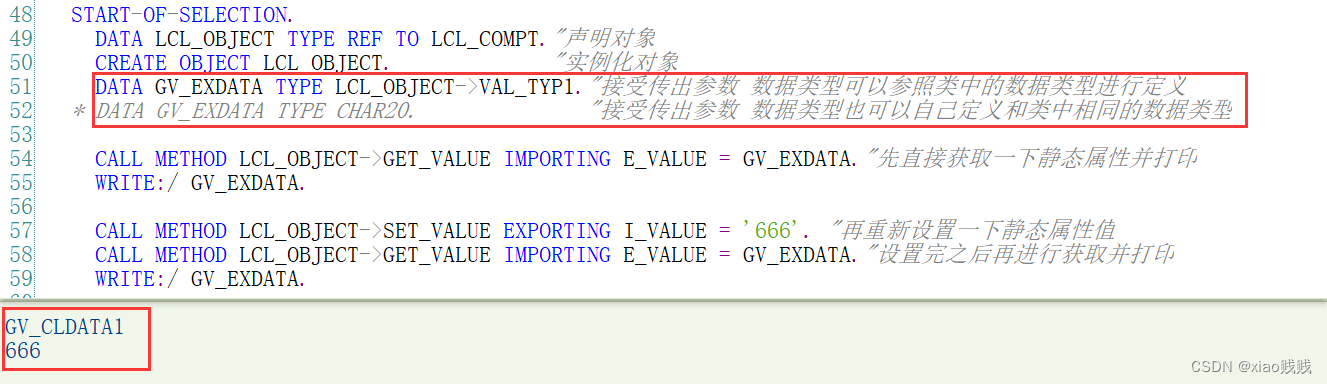
4.多参数的使用
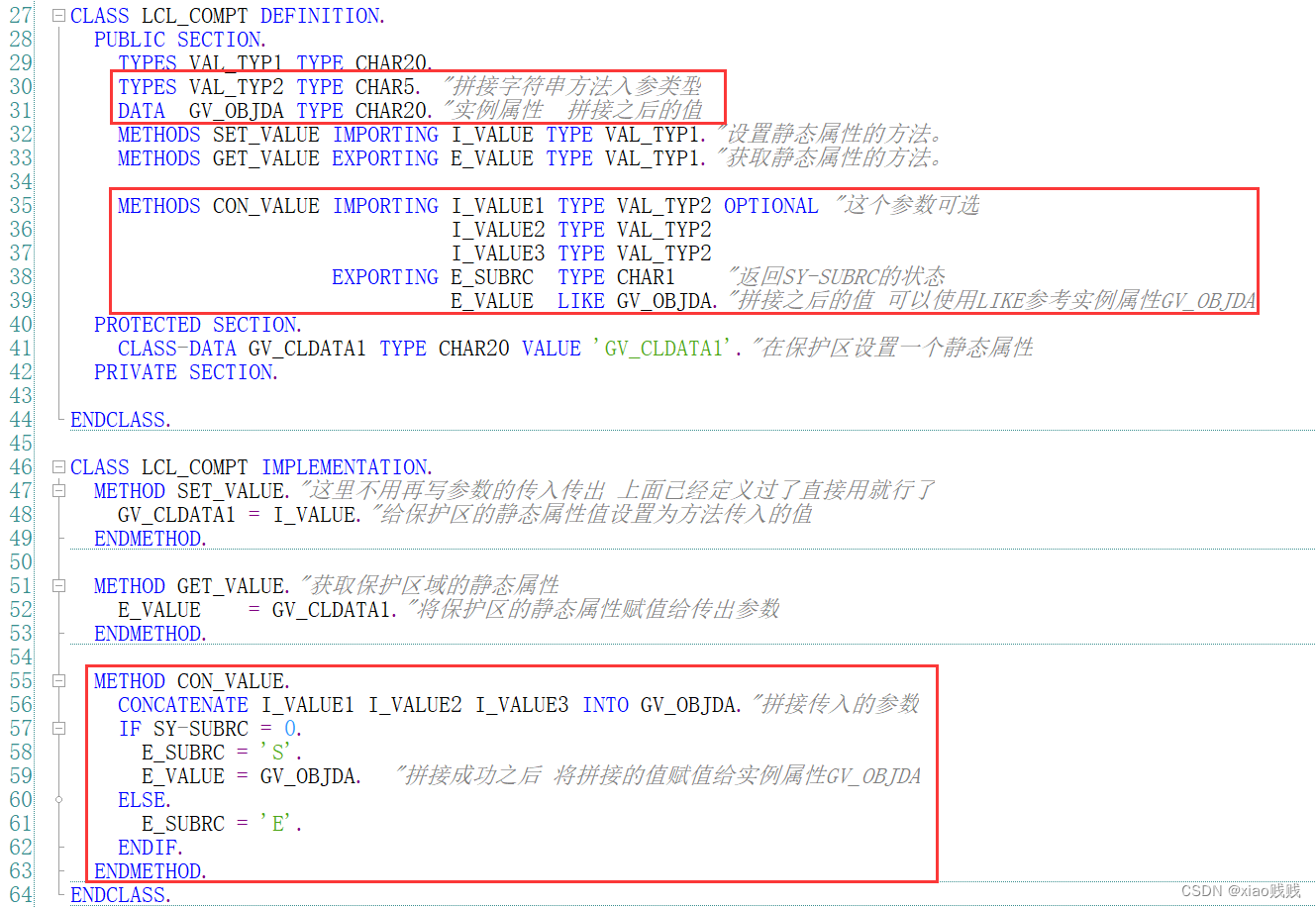
一个方法中可以同时 IMPORTING / EXPORTING 并且也都可以包含多个参数。我们再定义一个实例属性和实例方法。实例方法接收3个参数,传入后把这3个参数进行拼接赋值给实例属性,并且根据SY-SUBRC的值返回是否拼接成功标志。注意我们声明的方法其实和我们声明函数是一样的,EXPORTING 传出参数都是可选的,可以接收也可以不接收。在类中声明方法中的参数的时候也可以使用 OPTIONAL 后缀来定义这个参数是否必输。
a.定义
b.调用

c.运行结果
5.其他注意事项
当一个方法没有输出参数EXPORTING的时候可以通过以下方式调用
CALL METHOD method()."没有输入参数
CALL METHOD method()."一个输入参数
CALL METHOD method(f1 = a1 f2 = a2 fn = an)."N个输入参数
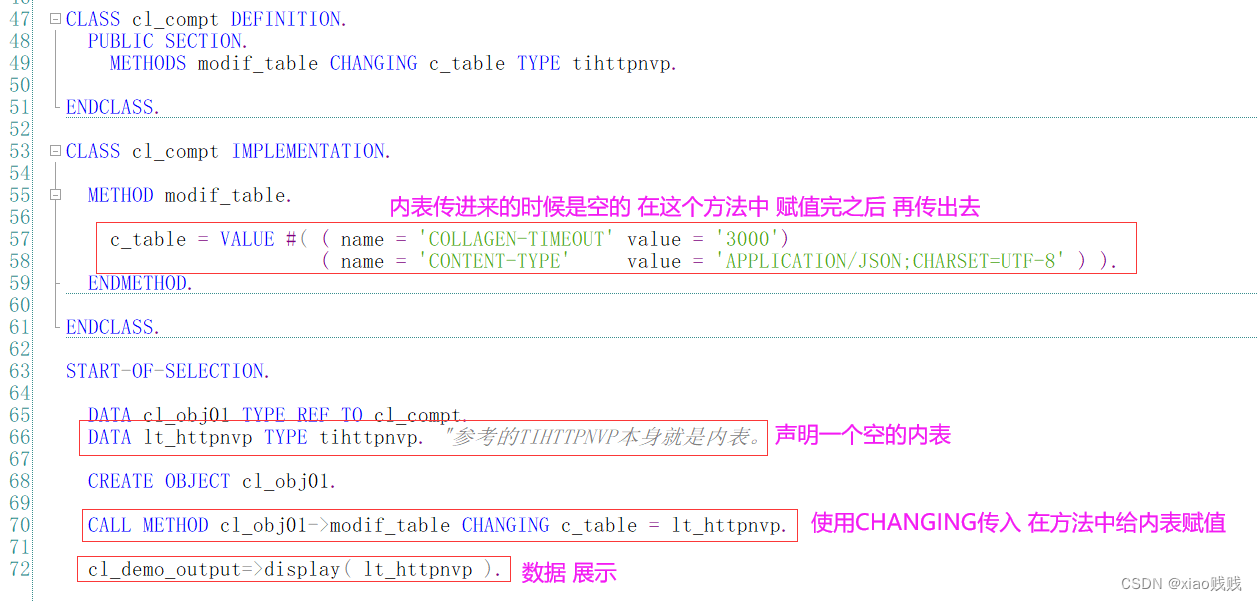
b.CHANGING
CHANGING是同时作为传入传出接口,接口参数可以参考单个变量 结构 或者内表。
1.传入内表
这就和 Perform 子程序的 用法没多大区别就不多做介绍了。
c.RETURNING
RETURNING是返回类 传递数值,该定义不能和CHANGING、EXPORTING同时使用,RETURNING 在返回参数的时候 必须使用 VALUE() 这样的后缀,表示用值传递,并且返回参数类型必须完整定义,如果类型定义为 C 这种不完整类型那么就会报错必须完整定义类型,我们其他传出传出参数的关键字也可以用VALUE表示值传递。RETURNING 的返回值在我们调用方法的时候要使用 RECEIVING来接收,并且RETURNING 只能定义一个形式参数作为返回参数。
1. 定义
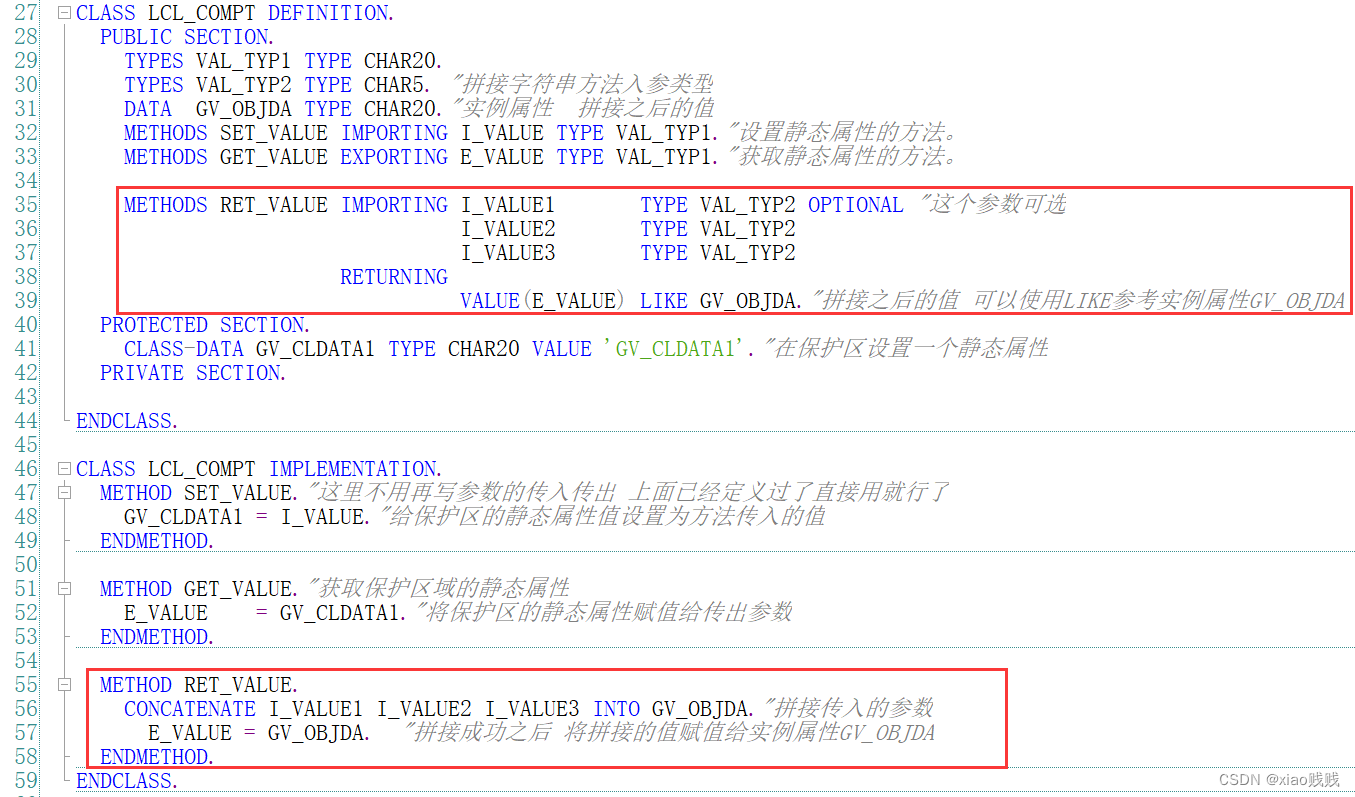
2. 调用 及 结果
如果方法中的返回值用了RETURNING,那么在调用该方法的时候还可以简写调用语句,如果传入参数只有一个值 只用给括号中填入传入参数,如果传入参数有多个值那么就得使用关键字一 一对应传参。简写调用语句详情请看本文 四-b-3

d.EXCEPTION
返回执行中所出现的错误抛出异常,具体使用方法请看本文 四-C
四、使用类做一个小案例
这个案例我们来用类做一个计算圆的面积的类,首先我们可以在类中的私有区域声明一个常量C_PI为圆周率3.14,在公共区域声明两个方法 一个CLA_PER方法用来计算圆的周长 有一个(IMPORTING)传入参数 I_R 为半径,一个(EXPORTING)传出参数E_PERIM为计算的周长,还有一个方法CLA_AREA 有一个(IMPORTING)传入参数 I_R为半径,一个(RETURNING)传出参数E_AREA为圆的面积。
a.CLA_PER 计算周长
1.定义
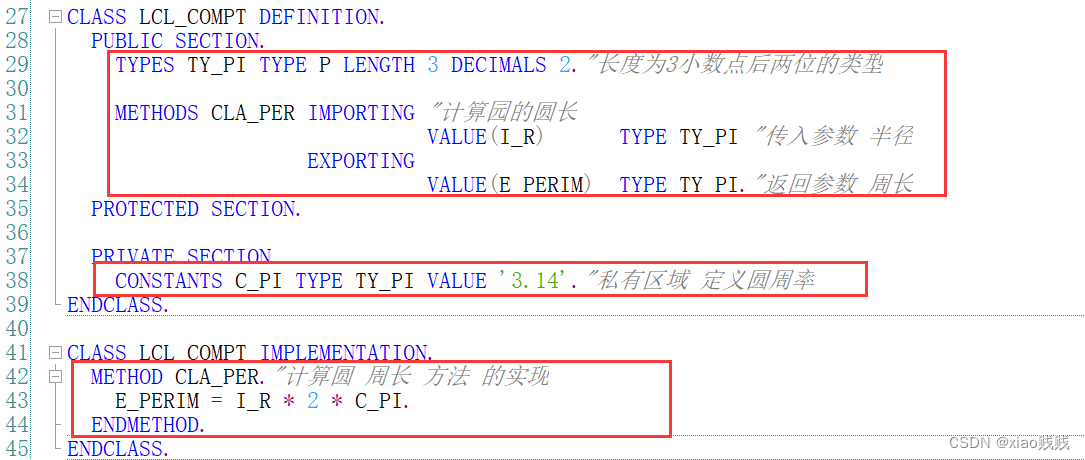
2.调用 及 结果
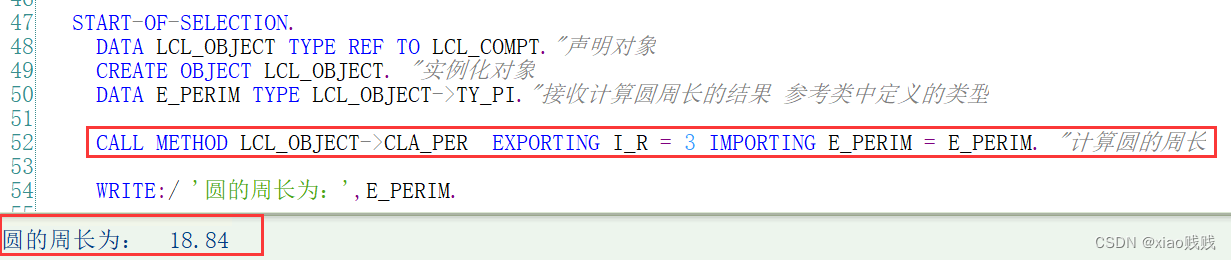
b.CLA_AREA 计算面积
1.定义
注意使用了RETURNING返回参数

2.调用 及 结果

3.调用(简化语法)

c.EXCEPTION 的应用
1.定义
在之前计算圆的面积方法中加入了 EXCEPTION 关键字 并定义 NO_LT_ZERO 异常 意思是不能小于0,在方法实现中首先对传入的半径进行判断小于0的话 直接用 RAISE 关键字抛出我们定义的这个异常。

2.调用
调用的时候用 EXCEPTION 关键字定义异常的编号,我们将 NO_LT_ZERO 这个异常定义为1,方法执行完可以用 SY-SUBRC 判断是否异常,如果 SY-SUBRC 为1的话就打印传入半径不能小于0。下面调用的时候我们半径传入的是-2所以为抛出异常1。并打印传入半径不能小于0。


五、抽象类
抽象类只需要在类中定义一些抽象方法, 而不用去定义具体的实现功能,抽象类中也可以定义非抽象方法并且编写方法的实现,从而被子类继承到。抽象类是 不能直接被参照实例化的。必须进行子类的派生继承之后才能去使用。
a.抽象类的定义
定义抽象类要使用关键字 ABSTRACT 定义抽象方法也要实用关键字 ABSTRACT。
1.定义 抽象类 抽象方法
下面这个抽象类中定义了一个实例方法一个抽象方法,抽象方法是不用写实现的,抽象类如果不用写任何其他方法的实现的话也不用写 IMPLEMENTATION 部分。

2.不写IMPLEMENTATION部分
我们只留一个抽象方法 去掉 IMPLEMENTATION 部分也是可以正常激活的 如图一所示。如果存在非抽象方法没有 IMPLEMENTATION 部分 是会报错的 如图二所示。下面我们会调用这个抽象方法。
图一

图二
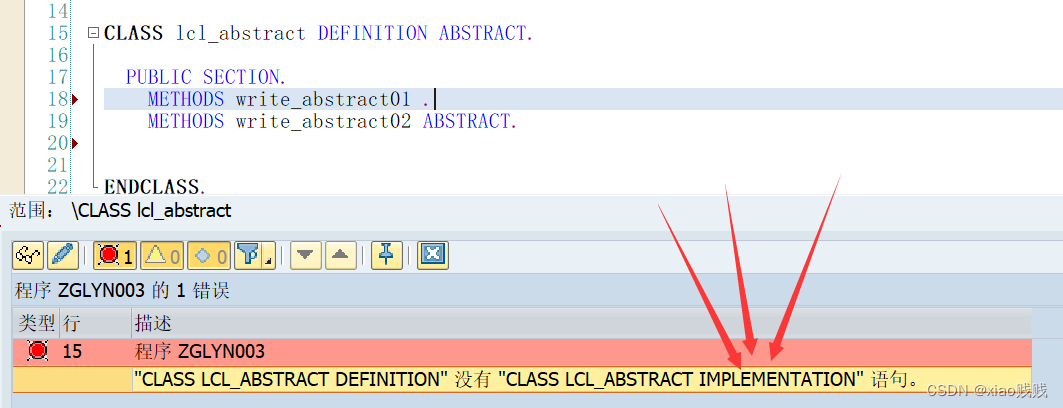
3.非抽象类中不能定义抽象方法
如果我们在一个非抽象类中也就是普通的类中定义一个抽象方法是会报错的。
b.抽象方法的使用
想要使用抽象方法那么就必须定义一个继承类,来继承抽象类,再到继承类中对抽象方法进行重写。
1.定义继承类

2.调用重写的方法
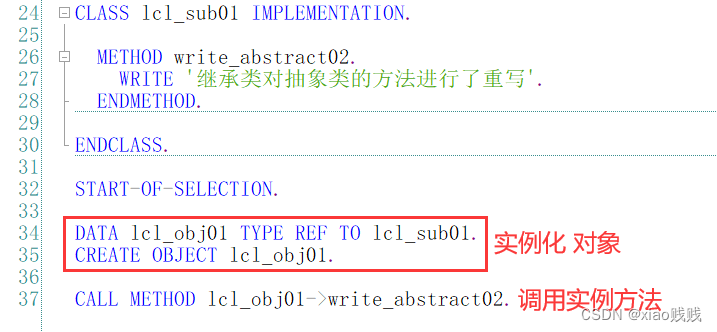
3.运行效果
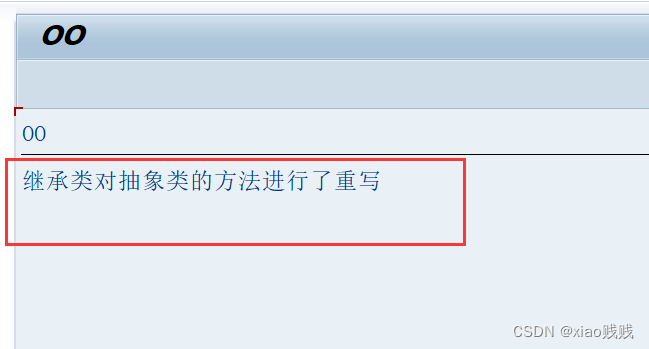
c.抽象类的作用 与 好处优点
通过使用抽象类,你可以创建一个灵活、可扩展和可维护的代码结构,从而使得代码更具适应性和重用性。
1.定义通用接口和行为
抽象类允许你定义一组通用的接口和行为,而不具体实现这些行为。这为子类提供了一个蓝图,使得子类可以按照需要去实现这些行为。
好处优点: 统一接口:所有子类都必须实现抽象类中定义的方法,确保接口一致性。灵活性:不同的子类可以根据具体需求实现不同的行为。
2.代码复用
抽象类可以包含具体的方法实现,这些方法可以被所有子类继承,从而避免重复代码。
好处优点: 减少重复代码:公共逻辑可以在抽象类中实现,子类只需实现特定的行为。提高代码维护性:公共逻辑集中在抽象类中,只需在一个地方修改,即可影响所有子类。
3.强制实现特定方法
抽象类可以定义抽象方法,这些方法必须在子类中实现,从而确保所有子类都有这些方法。
好处优点: 确保一致性:子类必须实现抽象方法,确保所有子类具有相同的基本功能。明确职责:子类必须实现抽象方法,使得子类的职责更加明确。
4.实现模板方法模式
抽象类可以定义模板方法,这些方法包含一系列步骤,其中某些步骤可以在抽象类中实现,而其他步骤则由子类实现。
好处优点: 复用算法:模板方法模式允许你定义算法的骨架,并将具体实现推迟到子类,从而实现代码复用。灵活扩展:子类可以根据需要重写某些步骤,而不影响算法的整体结构。
5.支持多态性
抽象类可以用作类型,使得可以通过抽象类引用不同子类的对象,从而实现多态性。
好处优点: 提高灵活性:可以在运行时决定具体使用哪个子类,从而实现更灵活的代码。简化代码:通过抽象类引用对象,可以简化代码逻辑,不需要关心具体的子类类型。
六、最终类
最终类很简单,作用就是防止由于设计中多级别派生造成类的语法和语义的冲突,不可被继承 的 叫做最终类,除了类,方法也可以单独的设置不能被继承。
a.最终类定义
1.定义
效果很明显报错提示不能有任何子类 。

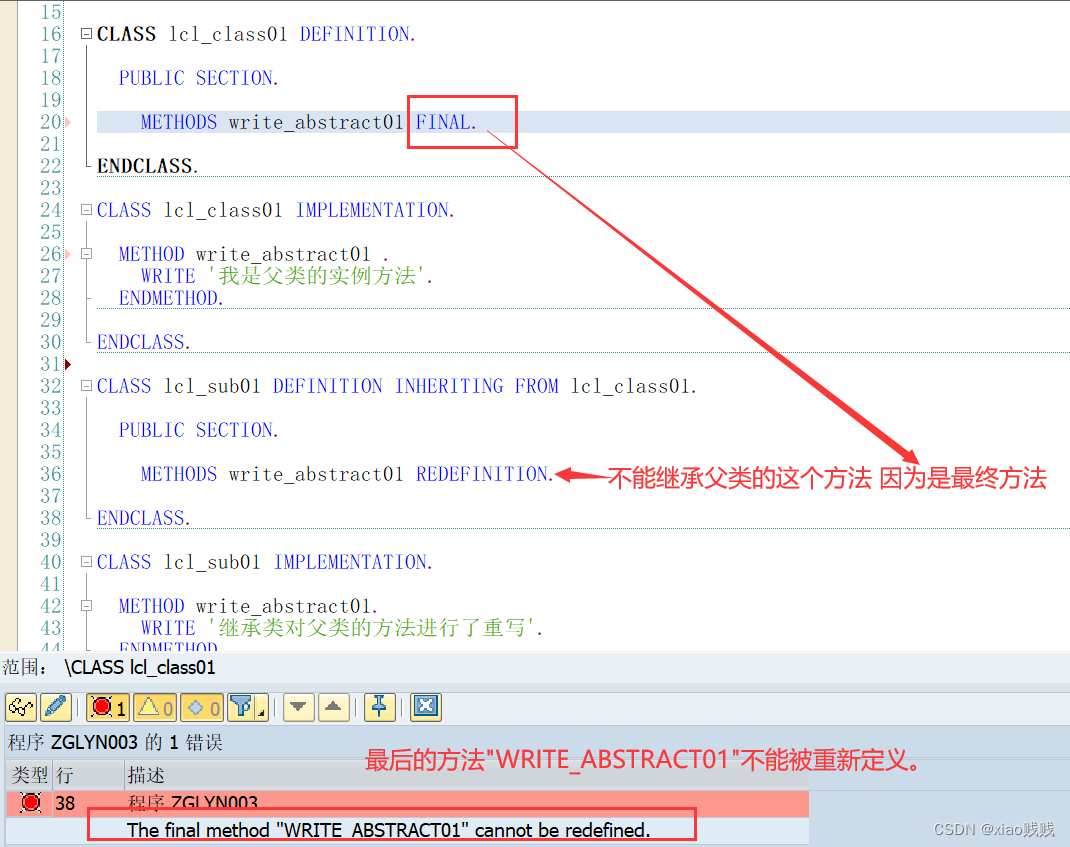
b.最终方法定义
1.定义
效果很明显报错提示这个方法不能被重新定义,当我们去掉FINAL关键字之后就可以正常激活了
七 、接口 (INTERFACE)
这里的接口指的是面向对象中的接口,不是我们SAP与其他系统集成所说的接口。完全是两个东西两码事。接口和抽象类是类似的,定义了一些 未实现的属性和方法,所有继承这个接口的类都继承了这个接口的所有成员,成员指的就是这些属性和方法 。
接口中定义的方法是不需要写实现部分的,所以接口也不能被实例化,接口的所有成员都是抽象的并且一般都是公有的,接口中不能含有构造方法,静态成员是可以有的。
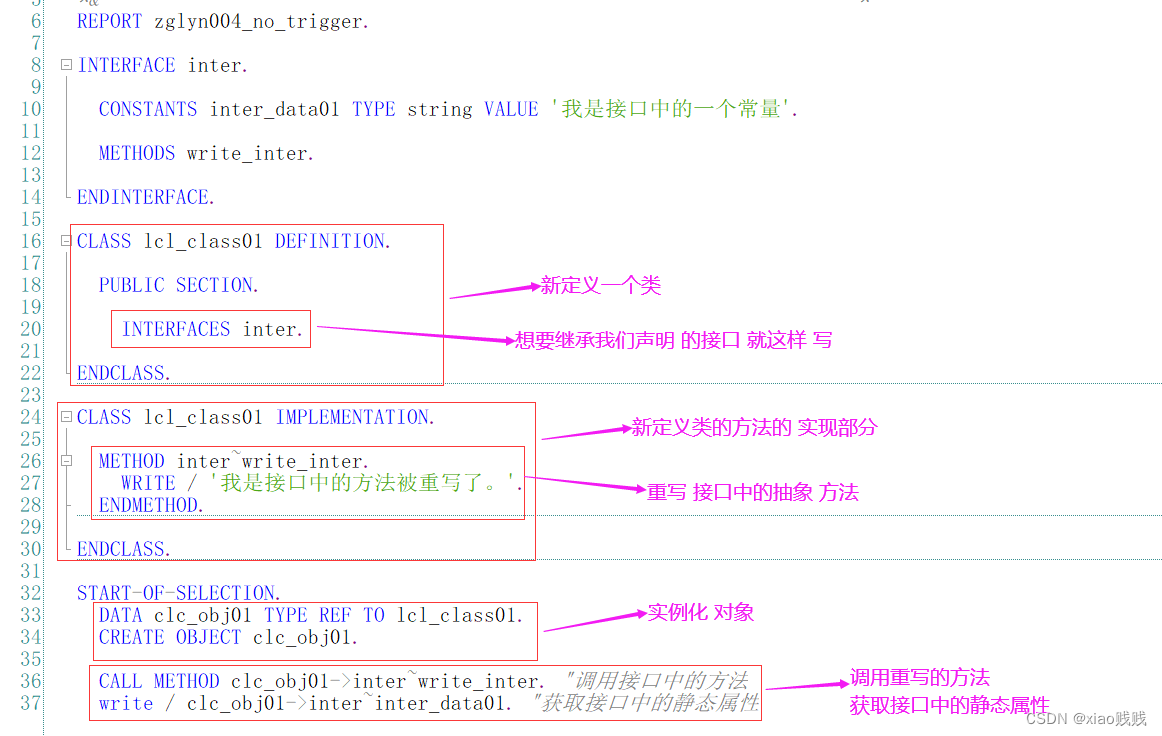
a.接口的定义
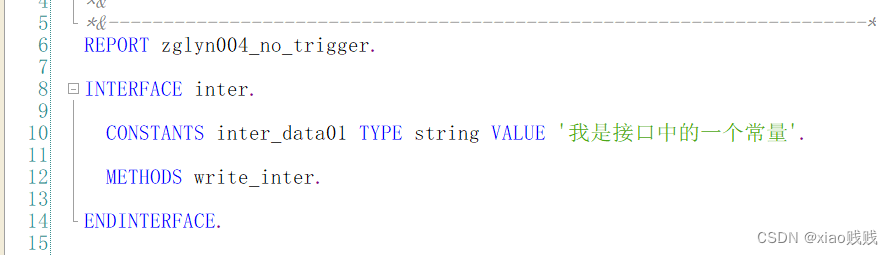
1.定义
接口的定义很简单,下面我们声明了一个接口 inter 这个接口里面有两个成员 一个是常量 inter_data01 一个是方法 write_inter,由于方法都是抽象的不用去实现的所以这样一个接口就定义好了。
b.接口的使用
注意调用接口中的重写方法的时候是 对象名->接口名~方法名
1.继承接口
2.结果
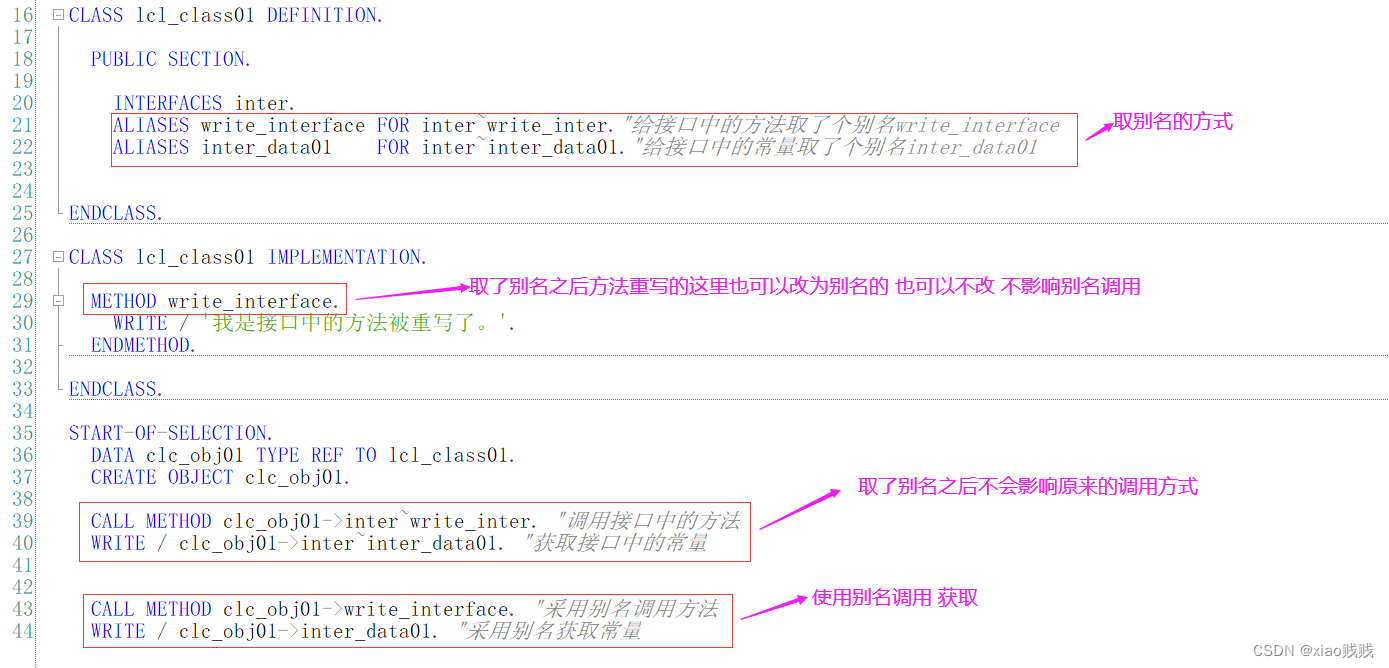
3.取别名
我们会发现在获取接口常量或者方法调用的时候书写名称会很麻烦尤其名字再长一点更不好看了。所以我们可以给接口中的这些成员取别名。如下图所示

c.接口的作用 与 好处优点
为什么要定义接口?比如说我们有同样的部分总是在许多类中去使用,我们第一种想法就是把 这些共同的部分定义到父类里面然后这些类都继承这个父类,但其实这样创建类是不灵活的它必须依靠这个父类才能创建就好像我们一个人只能有一个爸爸,如果我这个子类还想包含其他内容那么此时就不能实现了就不灵活了。所以我们可以将这些公用的部分定义在接口中,也能统一这些类使用这些成员的类型。
通过使用接口,开发者可以创建更灵活、可维护和可扩展的系统,确保各个组件之间能够良好协作,并且可以在不影响整体架构的情况下替换或修改具体实现。
1.实现多态性
多态性使得同一个方法可以有不同的实现,这有助于在运行时根据具体的对象类型执行适当的行为。
举例: 有一个接口叫 i_animal 意思是动物,这个接口有一个方法叫 make_sound 意思是发出声音,然后 再定义一个狗类和一个猫类,这两个类都继承 i_animal 接口,但是狗类中的make_sound方法会发出汪汪汪的声音而猫类中的make_sound方法会发出喵喵喵的声音,这就是一个方法可以有不同的实现叫做多态。
2.提高代码的可维护性和可扩展性
使用接口可以使代码更加模块化和可维护。通过定义接口,具体的实现可以在不影响接口用户的情况下进行修改或替换。这种松耦合设计使得系统更加灵活和可扩展。
3.定义统一的契约
接口提供了一种定义类必须实现的方法的方式,确保所有实现该接口的类都遵循相同的契约。这对于大型系统中各个组件之间的协作非常重要。
举例: 有一个接口叫 i_repository 意思是数据库,这个接口有三个方法分别是 save 保存数据、delete 删除数据、find 查找数据、然后 再定义一个file_repository (文件数据库)和一个 db_repository (db数据库),这两个类都继承 i_repository 接口,这样就保证了我这两个类都一定会有这三个方法。因为对于我这两个类来说他们必须实现这样的方法,才能满足我的系统或者业务的需求。
4.依赖注入
依赖注入 就拿上面的这个例子接着说,我们再定义一个 类 operate 这个类有一个 构造函数 需要传入的是一个对象,还有一个方法 fun01,这个方法中我们调用传入对象的方法 ,我们可以实例化一个操作文件的对象 file_repository01 然后再实例化 operate 对象的时候将file_repository01传入,此时我们再调用fun01方法的时候就是 文件操作了,如果我们传入的是db_repository对象,那么我们调用fun01方法的时候就是 db数据库操作了。
依赖注入(Dependency Injection,DI)是一种设计模式,用于实现对象之间的解耦。它允许将对象的依赖关系通过外部注入而不是在对象内部创建,从而提高代码的可维护性和可测试性。接口在依赖注入中扮演着重要角色,因为它们定义了可替换的契约,使得不同的实现可以互换。

REPORT zglyn004_no_trigger.
INTERFACE i_repository.METHODS save.METHODS delete.METHODS find.
ENDINTERFACE.CLASS file_repository DEFINITION.PUBLIC SECTION.INTERFACES i_repository.
ENDCLASS.CLASS file_repository IMPLEMENTATION.METHOD i_repository~save." 文件保存实现ENDMETHOD.METHOD i_repository~delete." 文件删除实现ENDMETHOD.METHOD i_repository~find." 文件查找实现ENDMETHOD.
ENDCLASS.CLASS db_repository DEFINITION.PUBLIC SECTION.INTERFACES i_repository.
ENDCLASS.CLASS db_repository IMPLEMENTATION.METHOD i_repository~save." 数据库保存实现ENDMETHOD.METHOD i_repository~delete." 数据库删除实现ENDMETHOD.METHOD i_repository~find." 数据库查找实现ENDMETHOD.
ENDCLASS.CLASS operate DEFINITION.PUBLIC SECTION.METHODS: constructor IMPORTING repository TYPE REF TO i_repository,fun01.PRIVATE SECTION.DATA: repository TYPE REF TO i_repository.
ENDCLASS.CLASS operate IMPLEMENTATION.METHOD constructor.me->repository = repository.ENDMETHOD.METHOD fun01.repository->save( ).ENDMETHOD.
ENDCLASS.START-OF-SELECTION.DATA file01 TYPE REF TO file_repository.CREATE OBJECT file01.DATA operate01 TYPE REF TO operate.CREATE OBJECT operate01EXPORTINGrepository = file01.operate01->fun01( ).DATA db01 TYPE REF TO db_repository.CREATE OBJECT db01.DATA operate02 TYPE REF TO operate.CREATE OBJECT operate02EXPORTINGrepository = db01.operate02->fun01( ).
八、事件
事件是面向对象中非常重要的一点
事件允许我们两个原本不相关的类之间发生功能。 之前我们说的是父类子类之间可能有点关联关系,事件就是两个完全不相关的类也可以去关联了,事件一般包含两个类,其中一个类叫 触发类 在这个类中呢可能到某个功能点会触发抛出一个事件,而另外一个类可以叫 捕获类 这个类我们去进行接收和捕获事件,这个捕获的类呢一旦发现触发类抛出了某个事件那么这个捕获类就可以执行相应的功能。
下面我们还是用一个案例来介绍事件,我们会定义一个触发类,这个触发类会有一个方法 get_all_num 这个方法有一个入参是 I 类型的,当我们传入30 这个方法会获取1到30的数字,当传入50会获取1到50。以此类推 ,当这get_all_num方法获取到的数字是偶数的时候就抛出一个事件叫 is_evennum ,然后我们再定义一个捕获类用来捕获我们这个事件并打印传递过来的数字。
a.触发类定义
触发类的定义主要用了 EVENTS、RAISE EVENT、这样的关键字。前者是用来定义一个事件的,后者是把定义的事件可以抛出的。
1.定义
主要看 51行 和 61行,我们需要把这个偶数用EXPORTING传给捕获的方法,捕获的方法使用IMPORTING去接收。

2.注意事项
1、事件定义的时候如果有参数需要传递使用的是EXPORTING并且必须使用VALUE进行值传递,同时抛出事件的时候也一样把我们想要传递的参数值用EXPORTING传递。
2、事件不一定要有参数的传递要看功能需求。如果定义的时候没有参数传递,那么相应的抛出和捕获的时候也就不要写参数。
b.捕获类定义
捕获类的定义主要用了 FOR EVENT ,SET HANDLER ,前者是在类中把触发类的事件 和 捕获类的方法进行关联的,后者是 把这种关联关系应用到实例对象上面,也叫注册事件,也就是说我触发类和捕获类的所有对象创建出来之后默认是没有这种关联触发关系的,我们必须给我们想要触发的对象再设置关联一遍。
1.定义
捕获类的定义是比较简单的主要看 72行 这句话的意思是:方法 write_evennum 是为了 事件 is_evennum 而写而服务的并且这个事件在类 cl_chufa 中定义着。记得接收响应的参数

2.注意事项
1、这里的捕获方法参数不需要写类型的参考,事件那边已经定义好了参考所以这个类型就是跟事件那边走的。
c.运行展示
首先我们先得有两个对象,我们得把在类中定义的这种事件关系落实到对象,因为最终我们是执行的是对象类又不能用来执行 。
1.实例化对象
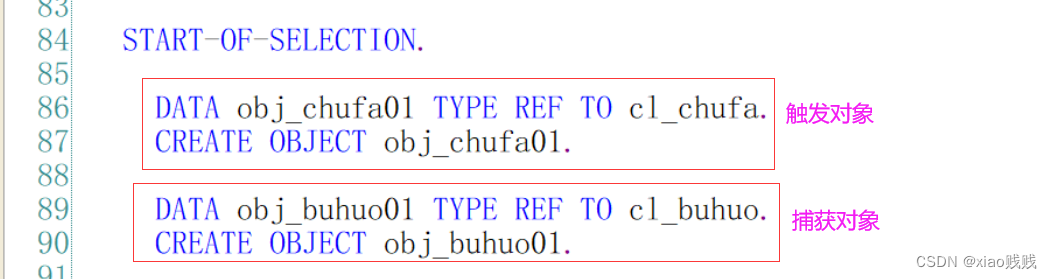
2.事件注册
SET HANDLER 将某个一个方法注册给某一个对象这一步非常重要,注意我们是用捕获方法 FOR 触发对象。顺序不要搞混了。这段代码的意思就是:我这个方法就是为你这个对象服务的。我就等着你抛出事件。

3.运行结果
可以看到我们1到32的所有 偶数都被打印了出来,而我调用的 get_all_num 方法里面并没有打印的操作。具体的执行过程可以打断点自己过一遍。
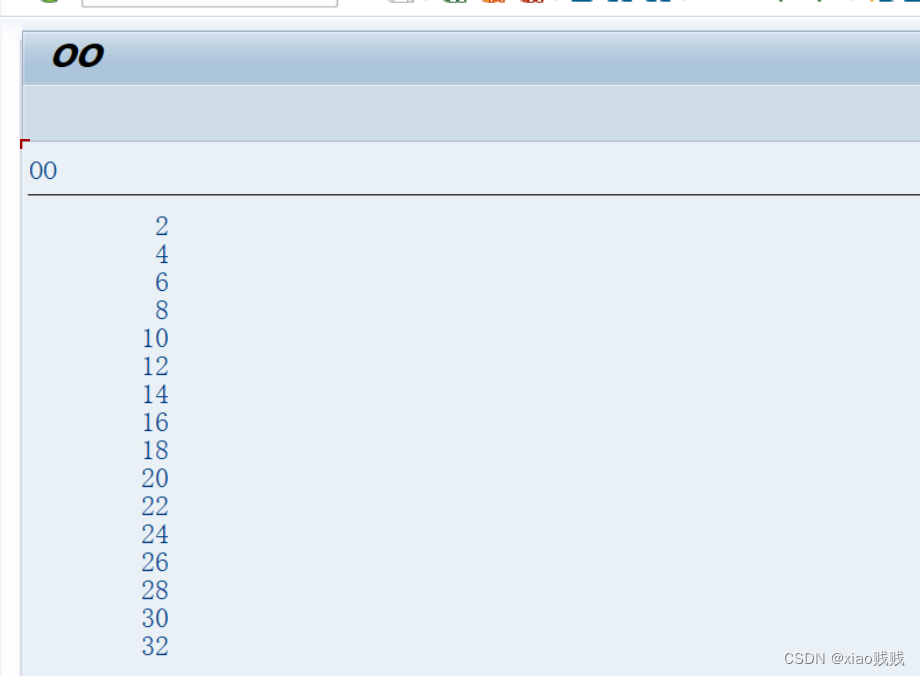
4.其他注意事项
我们可以再实例化一个触发对象 但是并不给这个触发对象注册绑定捕获方法。可以看到如果不注册就算是走到抛出事件这一步也不会跳转到我们这个捕获方法中来,大家可以打断点看一下的。运行结果没啥变化。
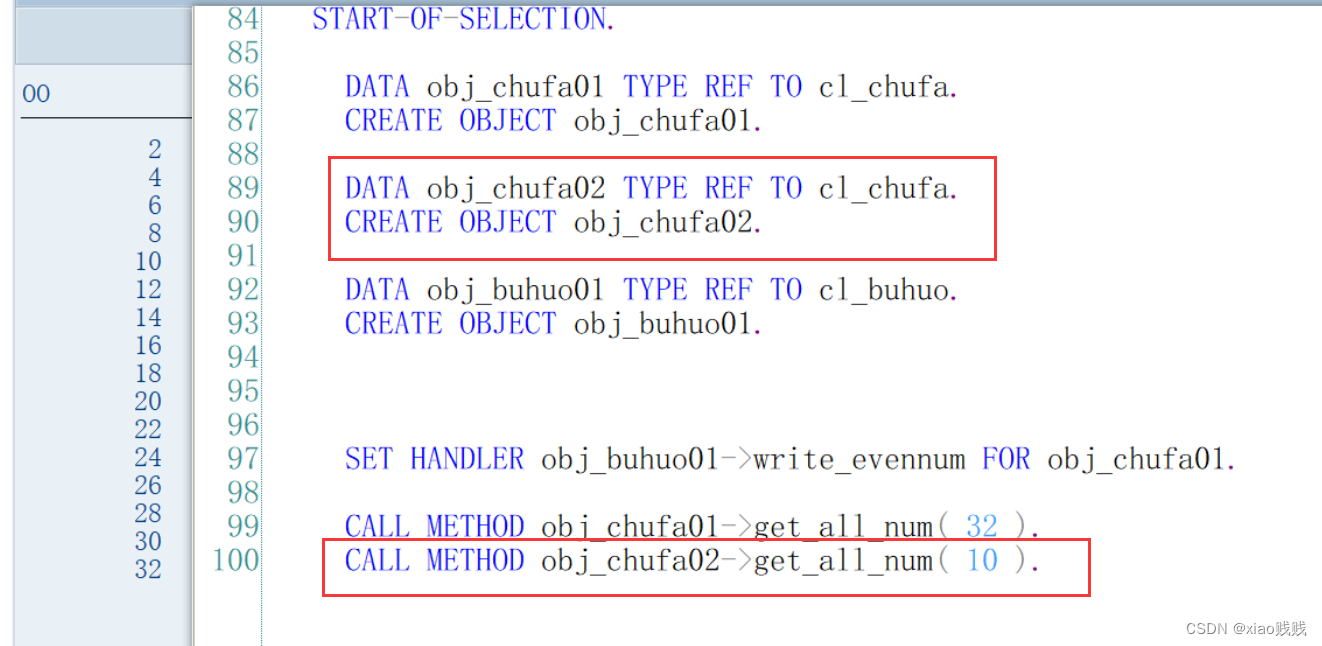
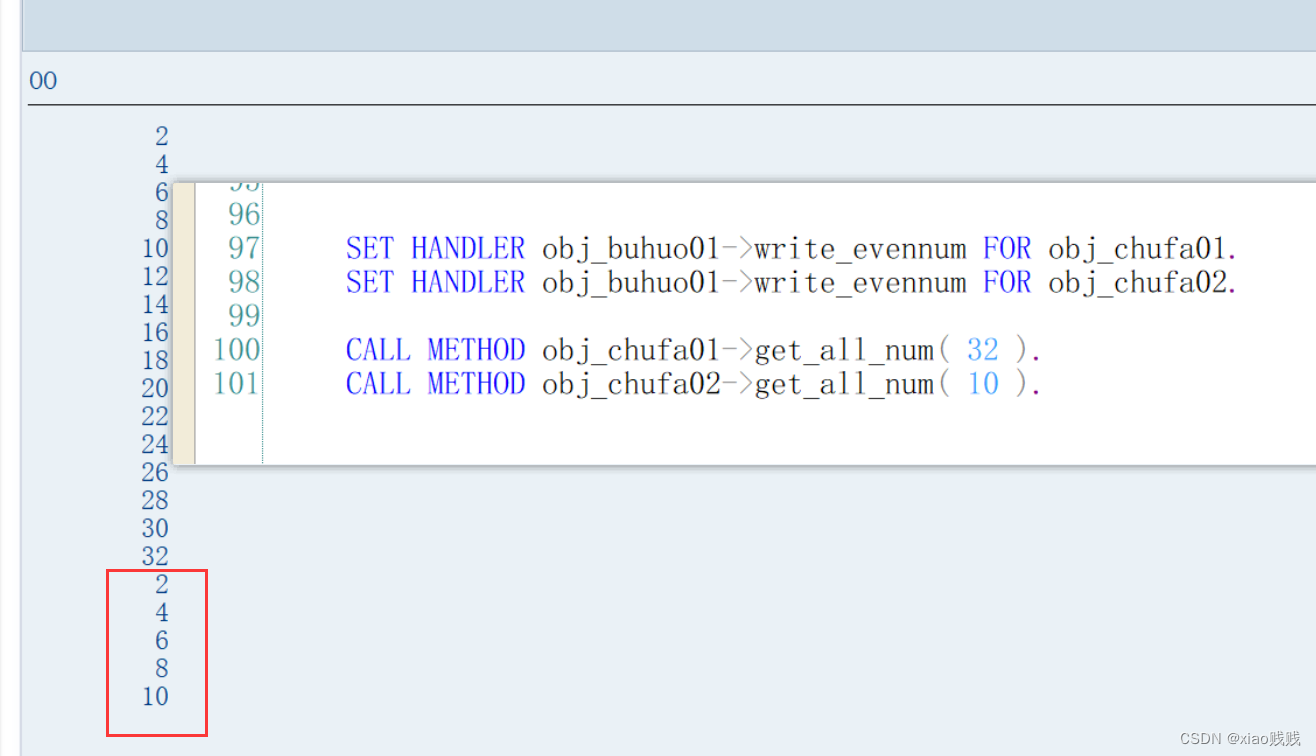
给obj_chufa02注册事件绑定捕获方法。
d.值得注意的点
由于我们是对象与对象之间绑定与注册 那么就涉及到一对多,多对一的情况。首先我们看这么一段比较官方的话:当程序执行到 RAISEEVENT 语句后,所有已注册的处理方法都将在下一个语句之前被处理。处理方法按照其在系统内部注册的顺序被执行。为避免无限循环,目前事件处理最多不能超过64级嵌套。
我来举例解释一下上面这句话,例如我们 is_evennum 事件不止打印偶数还想打印当前偶数的平方,那么此时我们就还得再来一个方法来绑定我们这个 is_evennum 事件,这个方法我们就叫做 write_evensqu。如果我们先在程序中给对象注册的是 write_evensqu 方法再注册 write_evennum 的方法 ,那么当事件is_evennum 被触发抛出之后程序会先把跟这个事件绑定注册的所有方法按照注册的先后顺序执行完才会执行 RAISEEVENT 之后的代码。也就是先会打印偶数平方再打印偶数再执行RAISEEVENT 之后的代码,由于我们上面RAISEEVENT 之后没有任何代码所以下面的示例我会加上。
1.不同的捕获方法给同一个触发对象注册
这个其实就是我上面所举的案例了。
a.代码的改动
触发类

捕获类

b.运行演示
write_evennum注册在前

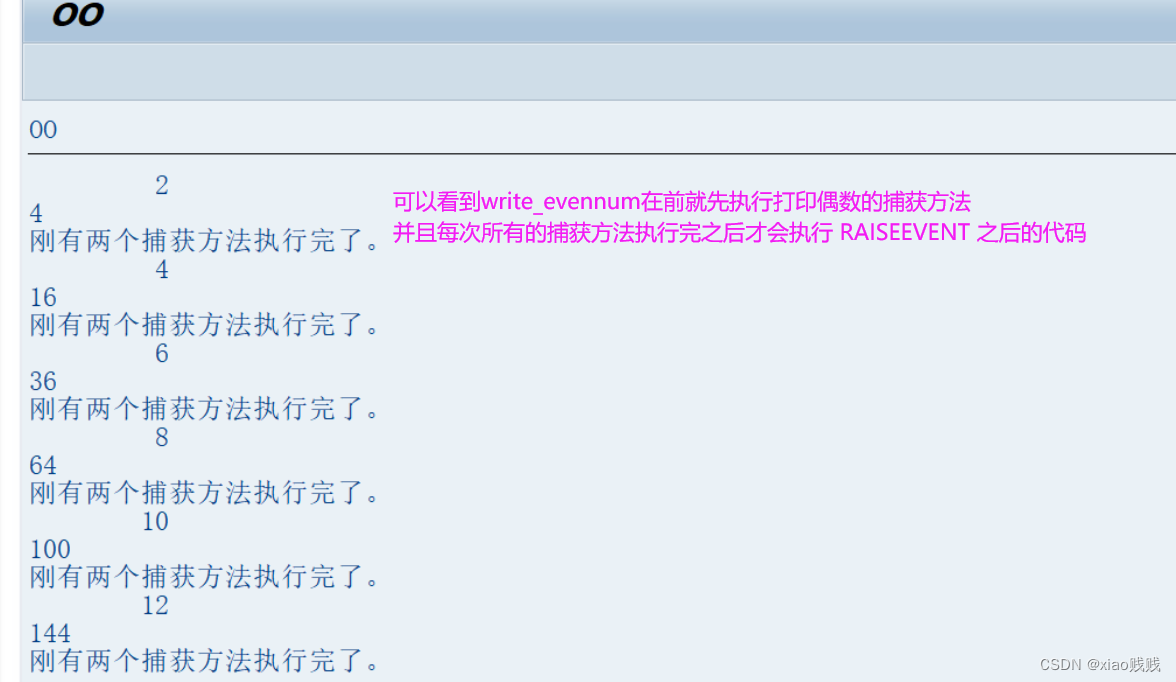
write_evensqu注册在前
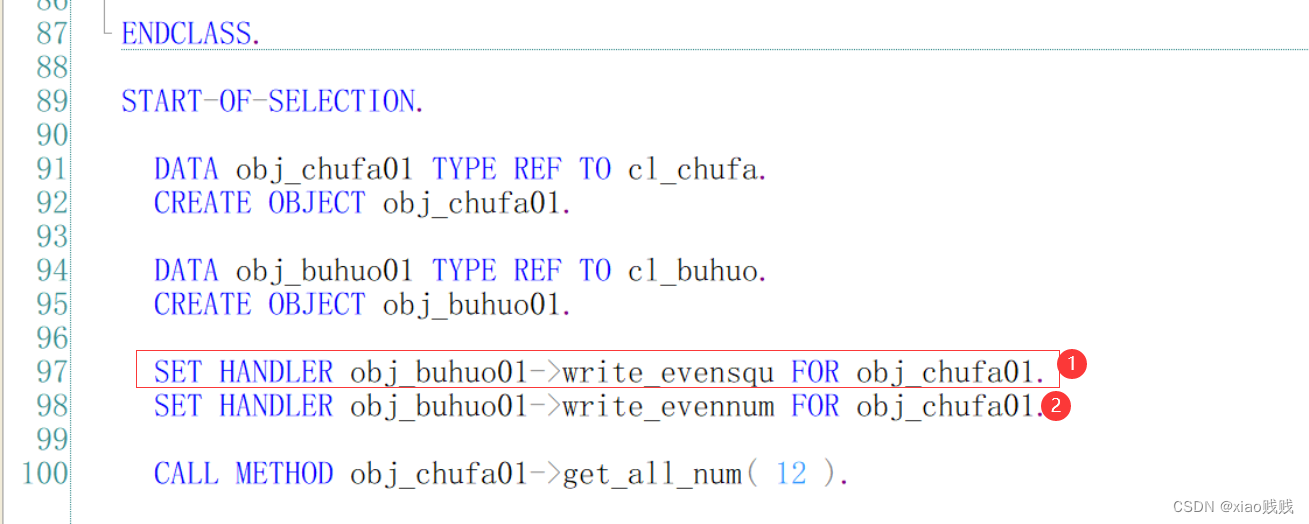
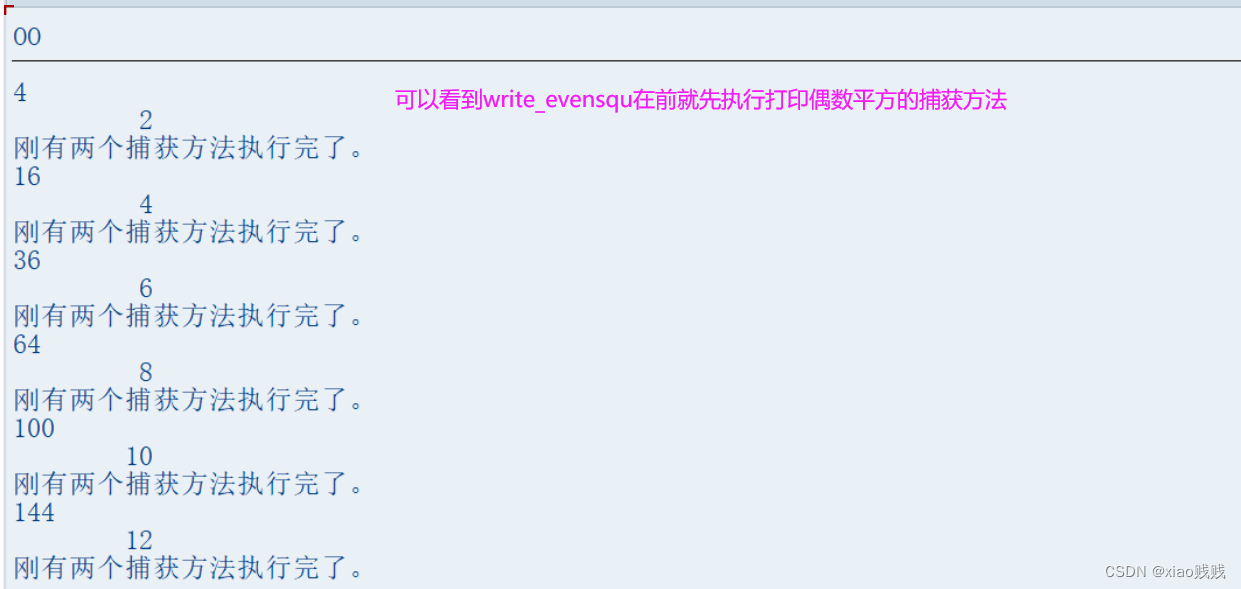
2.不同的捕获对象给同一个触发对象注册
这个其实也很好理解,就等于是我抛出事件之后被多个捕获对象捕获到了,这些捕获对象都会去执行相应已被注册的方法。
下面这个案例中有两个捕获对象,obj_buhuo01、obj_buhuo02,其中obj_buhuo01绑定注册了两个方法,那么事件被这个对象捕获到之后就会去执行这两个方法,obj_buhuo02绑定了一个捕获方法,那么事件被这个对象捕获到之后就回去执行被注册绑定的哪一个方法。而当我的事件抛出后会被这两个对象同时捕获到,捕获到之后这两个对象都会执行被注册绑定的方法。并且按照注册顺序执行 ,下面 哪个 “刚有两个捕获方法执行完了” 忘记改了 忽略即可 不重要

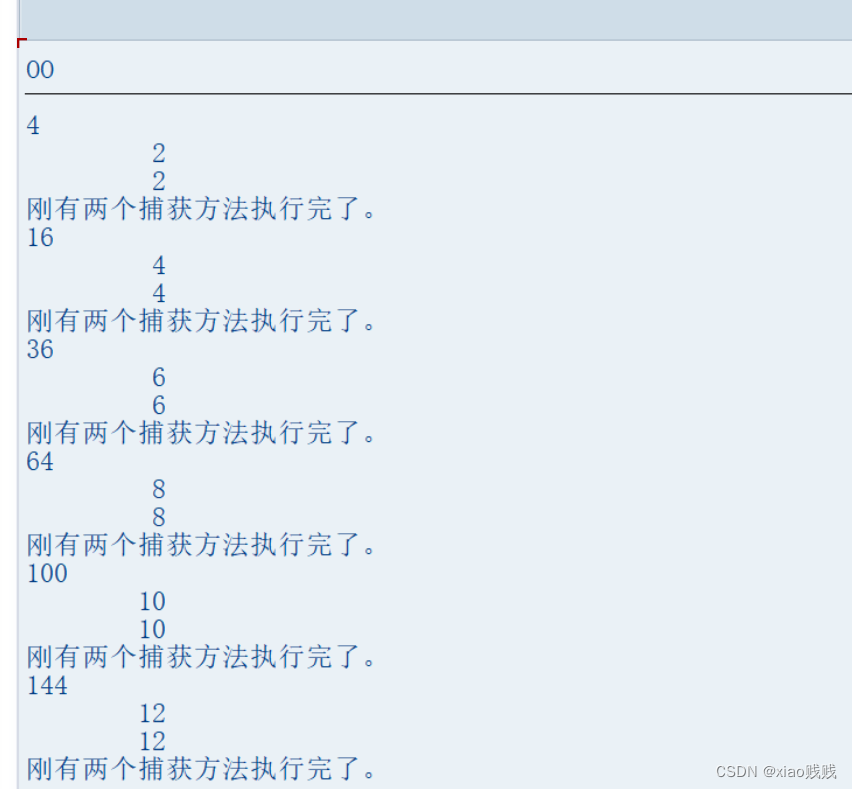
2.不同的触发对象给同一个捕获方法注册
这个就更好理解了,等于我不同的触发对象用的是同一个捕获对象。当我触发对象01抛出事件之后被捕获对象捕获到执行相应的注册方法即可,触发对象02抛出事件之后被捕获对象捕获到执行相应的注册方法即可。

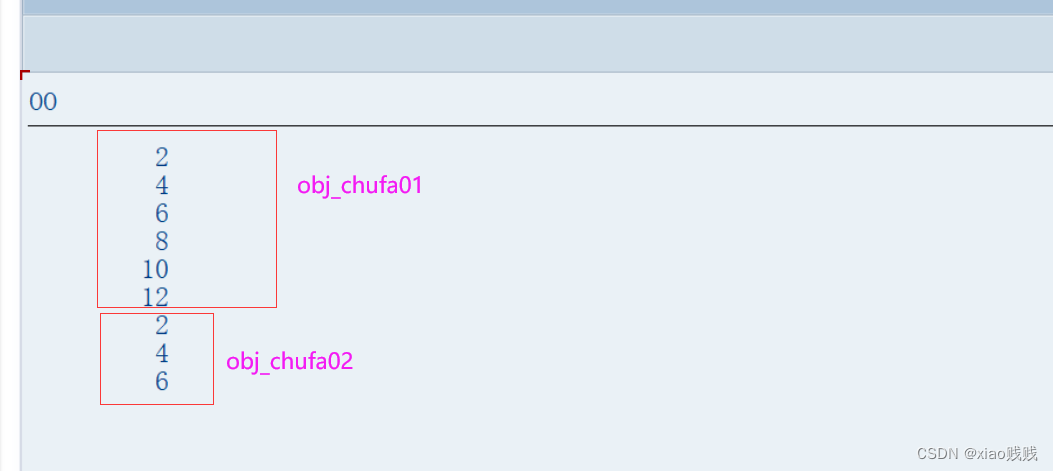
e.注册所有可以触发该事件的实例
还有一个事件注册的方式,是给所有的触发对象绑定捕获方法,我们还是接着上面的案例继续举例说明。
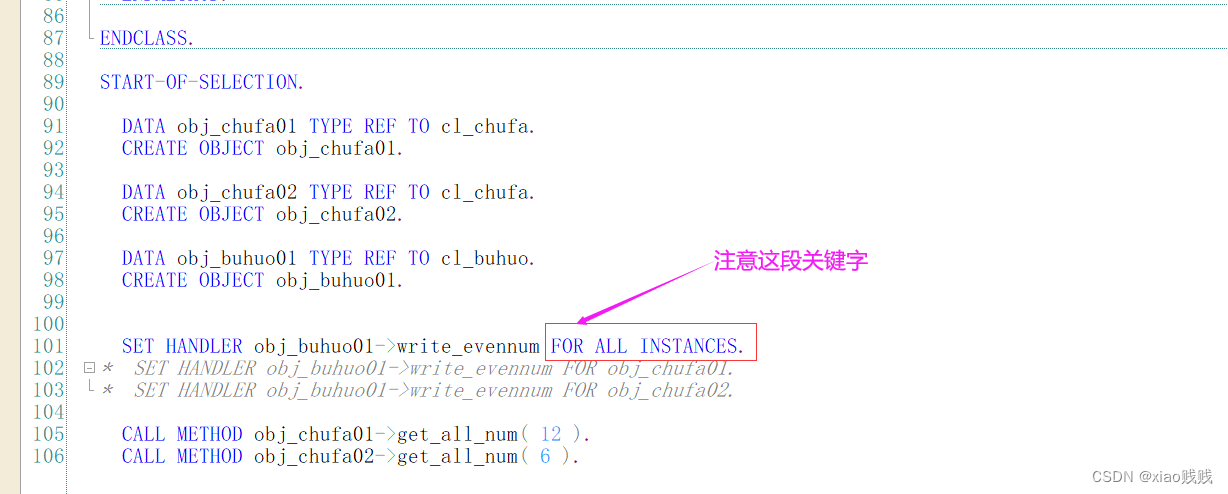
1.FOR ALL INSTANCES
下面只有一句注册事件的操作。
2.运行效果
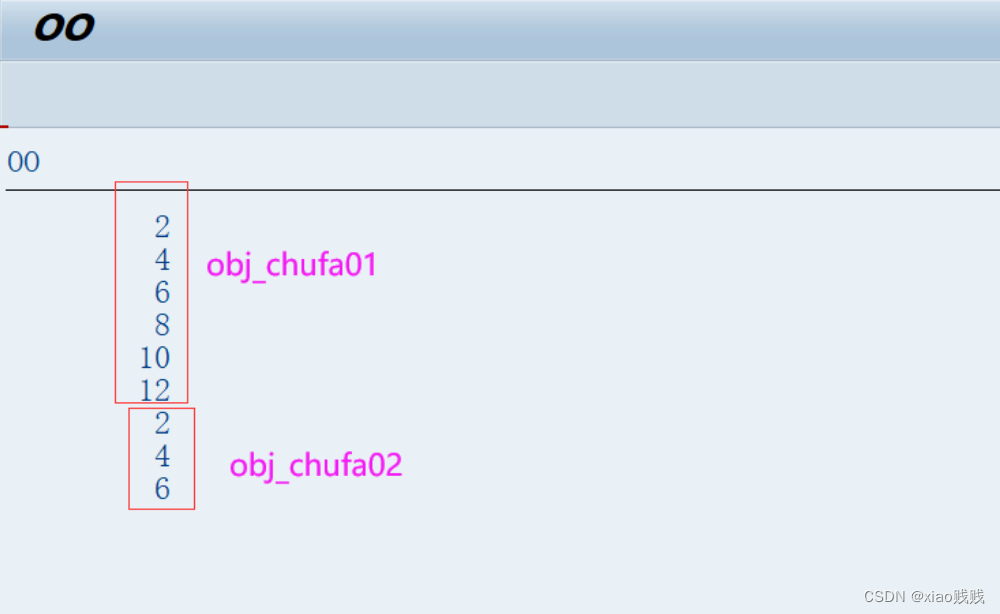
可以看到 就上面这一句话就给所有的实例对象注册了事件,我们有两个实例对象 obj_chufa01、obj_chufa02。正常应该要给这两个 对象都注册一遍,但是我们使用 FOR ALL INSTANCES 就可以给所有 对象注册了,也包括尚未被创建的实例。
3.Copy code
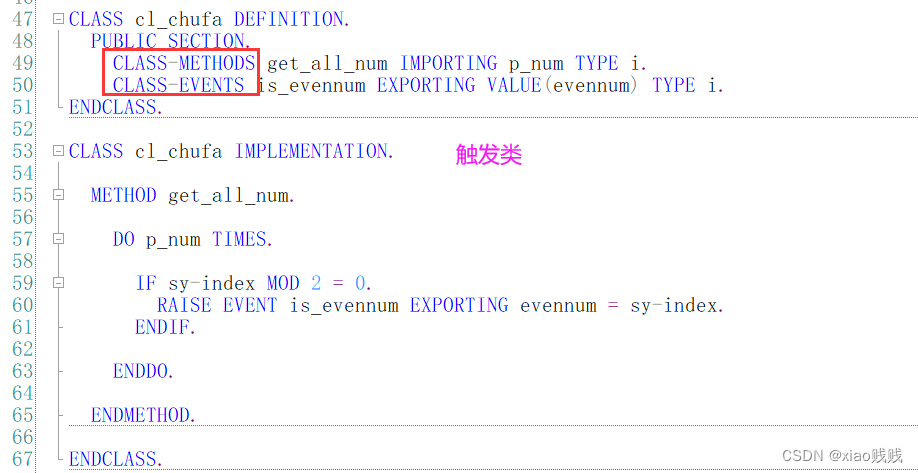
CLASS cl_chufa DEFINITION.PUBLIC SECTION.METHODS get_all_num IMPORTING p_num TYPE i.EVENTS is_evennum EXPORTING VALUE(evennum) TYPE i.
ENDCLASS.CLASS cl_chufa IMPLEMENTATION.METHOD get_all_num.DO p_num TIMES.IF sy-index MOD 2 = 0.RAISE EVENT is_evennum EXPORTING evennum = sy-index.
* WRITE /'刚有两个捕获方法执行完了。'.ENDIF.ENDDO.ENDMETHOD.ENDCLASS.CLASS cl_buhuo DEFINITION.PUBLIC SECTION.METHODS write_evennum FOR EVENT is_evennum OF cl_chufa IMPORTING evennum.METHODS write_evensqu FOR EVENT is_evennum OF cl_chufa IMPORTING evennum.
ENDCLASS.CLASS cl_buhuo IMPLEMENTATION.METHOD write_evennum.WRITE / evennum .ENDMETHOD.METHOD write_evensqu.WRITE / |{ evennum * evennum }|.ENDMETHOD.ENDCLASS.START-OF-SELECTION.DATA obj_chufa01 TYPE REF TO cl_chufa.CREATE OBJECT obj_chufa01.DATA obj_chufa02 TYPE REF TO cl_chufa.CREATE OBJECT obj_chufa02.DATA obj_buhuo01 TYPE REF TO cl_buhuo.CREATE OBJECT obj_buhuo01.SET HANDLER obj_buhuo01->write_evennum FOR ALL INSTANCES.
* SET HANDLER obj_buhuo01->write_evennum FOR obj_chufa01.
* SET HANDLER obj_buhuo01->write_evennum FOR obj_chufa02.CALL METHOD obj_chufa01->get_all_num( 12 ).CALL METHOD obj_chufa02->get_all_num( 6 ).
f.静态事件
事件类型分为4种:1、 定义在类中的实例事件 2、 定义在类中的静态事件 3、 定义在接口中的实例事件 4、 定义在接口中的静态事件。下面我们再演示一下类中的静态事件也是比较简单的。只是有些点需要注意。接口大家可以自己去研究实践一下。
1.直接在原来的基础上做修改
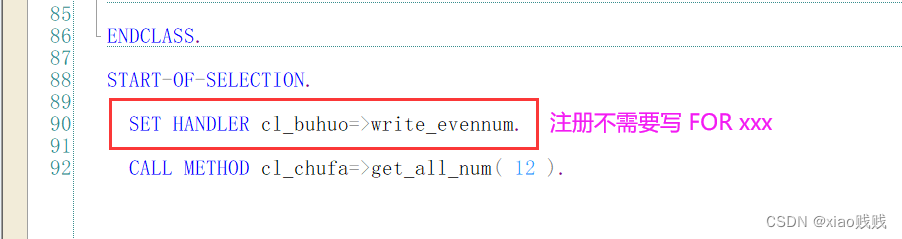
注意下图中的标注即可,静态事件,可以使用 CLASS-EVENTS 关键字,静态事件在静态方法中触发抛出,并且只能由静态事件处理程序处理。也就是捕获这个事件的方法也必须是静态方法。注册的时候不需要加FOR后缀自动应用整个类 ,注册和调用的时候记得使用=>。

2.运行效果

九、总结
以上就是今天要讲的内容,本文仅仅简单介绍了ABAP 的面向对象 ,感觉笔者讲的好对自己有帮助的还麻烦点个免费的赞赞制作不易谢谢谢谢!!!如果有说错或者不好的地方还望大家提出来见谅。感觉笔者写的好的别忘了关注点赞加评论哦,也欢迎大家一起来讨论。谢谢!
