易语言怎么做点击按钮打开网站做H5哪个网站字体漂亮一些
基于JavaWeb+SSM+Vue停车场微信小程序系统的设计和实现
- 滑到文末获取源码
- Lun文目录
- 前言
- 主要技术
- 系统设计
- 功能截图
- 订阅经典源码专栏
- Java项目精品实战案例《500套》
- 源码获取
滑到文末获取源码
Lun文目录
目录
1系统概述 1
1.1 研究背景 1
1.2研究目的 1
1.3系统设计思想 1
2相关技术 2
2.1微信小程序 2
2.2 MYSQL数据库 3
2.3 uni-app 3
2.4 SSM框架简介 4
3系统分析 5
3.1可行性分析 5
3.1.1技术可行性 6
3.1.2经济可行性 6
3.1.3操作可行性 6
3.2系统性能分析 6
3.2.1 系统安全性 6
3.2.2 数据完整性 7
3.3系统界面分析 7
3.4系统流程和逻辑 8
4系统概要设计 9
4.1概述 9
4.2系统结构 10
4.3.数据库设计 10
4.3.1数据库实体 10
4.3.2数据库设计表 12
5系统详细实现 17
5.1 管理员模块的实现 17
5.1.1 车主信息管理 17
5.1.2 商家信息管理 17
5.1.3 预约停车管理 18
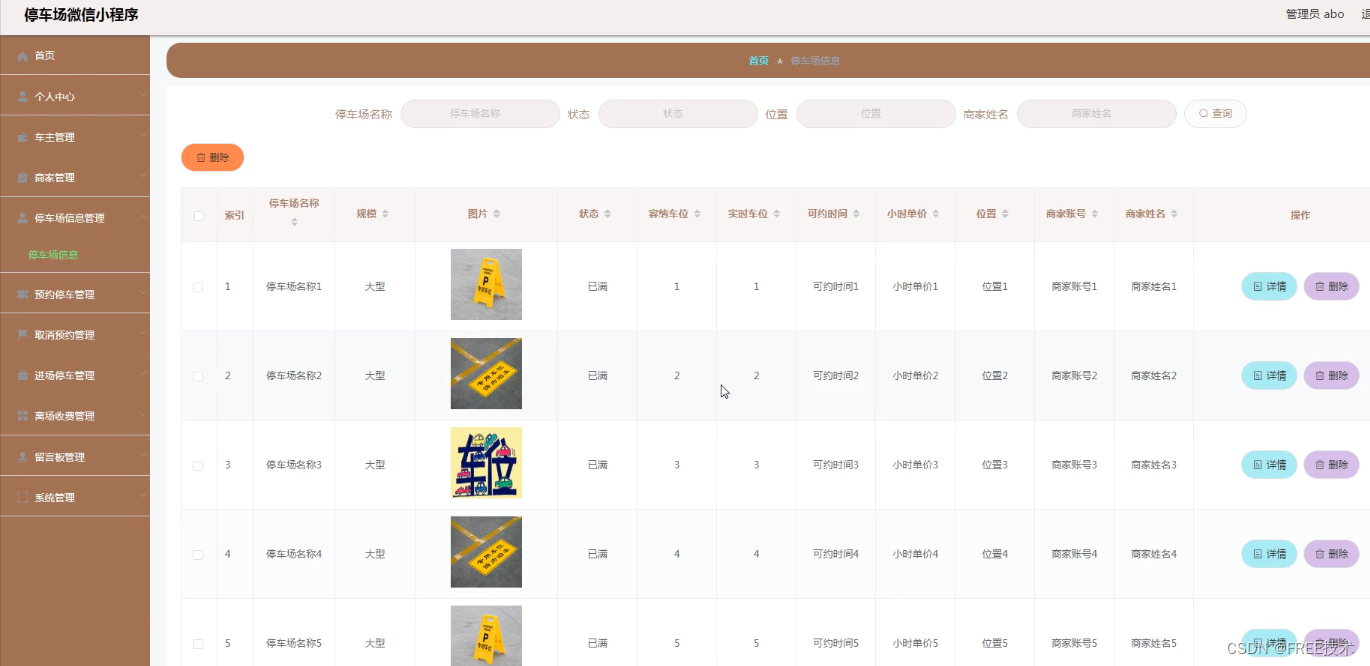
5.2.2 停车场信息管理 18
5.2 小程序用户模块的实现 19
5.2.1 商家审核 19
5.2.2 我的 20
5.2.3 停车订单 21
6系统测试 23
6.1概念和意义 23
6.2特性 23
6.3重要性 24
6.4测试方法 24
6.5 功能测试 24
6.6可用性测试 25
6.7性能测试 25
6.8测试分析 26
6.9测试结果分析 26
结论 26
致谢语 27
参考文献 27
前言
随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了停车场微信小程序的开发全过程。通过分析停车场微信小程序管理的不足,创建了一个计算机管理停车场微信小程序的方案。文章介绍了停车场微信小程序的系统分析部分,包括可行性分析等,系统设计部分主要介绍了系统功能设计和数据库设计。
本停车场微信小程序有管理员,用户,以及商家三个角色。管理员功能有个人中心,车主管理,商家管理,停车场信息管理,预约停车管理,取消预约管理,进场停车管理,商场收费管理,留言板管理,系统管理等。商家可以提交停车信息,用户可以停车。因而具有一定的实用性。
本站后台采用Java的SSM框架进行后台管理开发,可以在浏览器上登录进行后台数据方面的管理,MySQL作为本地数据库,微信小程序用到了微信开发者工具,充分保证系统的稳定性。系统具有界面清晰、操作简单,功能齐全的特点,使得停车场微信小程序管理工作系统化、规范化。
关键词:停车场微信小程序;SSM框架;MYSQL数据库
主要技术
2.1微信小程序
小程序是一种新的开放能力,开发者可以快速地开发一个小程序。小程序可以在微信内被便捷地获取和传播,同时具有出色的使用体验。尤其拥抱微信生态圈,让微信小程序更加的如虎添翼,发展迅猛。
2.2 MYSQL数据库
MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常适用于Web站点或者其他应用软件的数据库后端的开发工作。此外,用户可利用许多语言编写访问MySQL数据库的程序。作为开放源代码运动的产物之一,MySQL关系数据库管理系统越来越受到人们的青睐,应用范围也越来越广。速度和易用性使MySQL特别适用于Web站点或应用软件的数据库后端的开发工作。
MYSQL数据库具有以下特点:
1、C和C ++中使用和测试,以确保源代码的编译器的便携性和灵活性。
2、支持多种操作系统AIX的,FreeBSD下,HP-UX,Linux和Mac OS中,Novell公司的Netware,OpenBSD系统,OS/2裹时,Solaris,Windows等。
3、提供了用于不同的编程语言的API。编程语言,如C, C ++,Python和Java的,的Perl,PHP,埃菲尔铁塔,Ruby和Tcl的。
4、以及使用的CPU资源来支持多线程。
5、算法优化查询SQL,切实提高搜索速度。
6、网络上的客户端和服务器可以用来编程任何独立的编程环境,也有中国,GB2312,BIG5,日文写作,一般基金,用于支持多国语言,并且可以嵌入在数据表和其他软件shift_jis访问柱可以用作的名称。
7、TCP / IP,ODBC和JDBC数据库,并提供连接到其他。
8、管理工具的管理,控制和优化数据库的操作。
9、可以数以千万计的记录在一个大的数据库。
2.3 uni-app
uni-app 是一个使用 Vue.js 开发所有前端应用的框架,开发者编写一套代码,可发布到iOS、Android、Web(响应式)、以及各种小程序(微信/支付宝/百度/头条/QQ/钉钉/淘宝)、快应用等多个平台。
DCloud公司拥有800万开发者、数百万应用、12亿手机端月活用户、数千款uni-app插件。
uni-app在手,做啥都不愁。即使不跨端,uni-app也是更好的小程序开发框架更好的App跨平台框架、更方便的H5开发框架。不管领导安排什么样的项目,你都可以快速交付,不需要转换开发思维、不需要更改开发习惯。
2.4 SSM框架简介
SSM框架,是Spring+Spring MVC+MyBatis的缩写,这个是继SSH之后,目前比较主流的Java EE企业级框架,适用于搭建各种大型的企业级应用系统。
1.Spring简介
Spring是一个开源框架,Spring是于2003年兴起的一个轻量级的Java开发框架,由Rod Johnson在其著作Expert One-On-One J2EE Development and Design中阐述的部分理念和原型衍生而来。它是为了解决企业应用开发的复杂性而创建的。Spring使用基本的JavaBean来完成以前只可能由EJB完成的事情。然而,Spring的用途不仅限于服务器端的开发。从简单性、可测试性和松耦合的角度而言,任何Java应用都可以从Spring中受益。简单来说,Spring是一个轻量级的控制反转(IoC)和面向切面(AOP)的容器框架。
A.控制反转(IOC)是什么呢?
IOC:控制反转也叫依赖注入。利用了工厂模式将对象交给容器管理,你只需要在spring配置文件总配置相应的bean,以及设置相关的属性,让spring容器来生成类的实例对象以及管理对象。在spring容器启动的时候,spring会把你在配置文件中配置的bean都初始化好,然后在你需要调用的时候,就把它已经初始化好的那些bean分配给你需要调用这些bean的类(假设这个类名是A),分配的方法就是调用A的setter方法来注入,而不需要你在A里面new这些bean了。
B.面向切面(AOP)又是什么呢?
首先,需要说明的一点,AOP只是Spring的特性,它就像OOP一样是一种编程思想,并不是某一种技术,AOP可以说是对OOP的补充和完善。OOP引入封装、继承和多态性等概念来建立一种对象层次结构,用以模拟公共行为的一个集合。当我们需要为分散的对象引入公共行为的时候,OOP则显得无能为力。也就是说,OOP允许你定义从上到下的关系,但并不适合定义从左到右的关系。例如日志功能。日志代码往往水平地散布在所有对象层次中,而与它所散布到的对象的核心功能毫无关系。在OOP设计中,它导致了大量代码的重复,而不利于各个模块的重用。将程序中的交叉业务逻辑(比如安全,日志,事务等),封装成一个切面,然后注入到目标对象(具体业务逻辑)中去。
实现AOP的技术,主要分为两大类:一是采用动态代理技术,利用截取消息的方式,对该消息进行装饰,以取代原有对象行为的执行;二是采用静态织入的方式,引入特定的语法创建“方面”,从而使得编译器可以在编译期间织入有关“方面”的代码。
2.Spring MVC简介
Spring MVC属于Spring Framework的后续产品,已经融合在Spring Web Flow里面,它原生支持的Spring特性,让开发变得非常简单规范。Spring MVC分离了控制器、模型对象、分派器以及处理程序对象的角色,这种分离让它们更容易进行定制。
3.MyBatis简介
MyBatis本是apache的一个开源项目iBatis,2010年这个项目由apache software foundation迁移到了google code,并且改名为MyBatis。MyBatis是一个基于Java的持久层框架。iBATIS提供的持久层框架包括SQL Maps和Data Access Objects(DAO)MyBatis消除了几乎所有的JDBC代码和参数的手工设置以及结果集的检索。MyBatis使用简单的XML或注解用于配置和原始映射,将接口和Java的POJOs(Plain Old Java Objects,普通的Java对象)映射成数据库中的记录。可以这么理解,MyBatis是一个用来帮你管理数据增删改查的框架。
系统设计
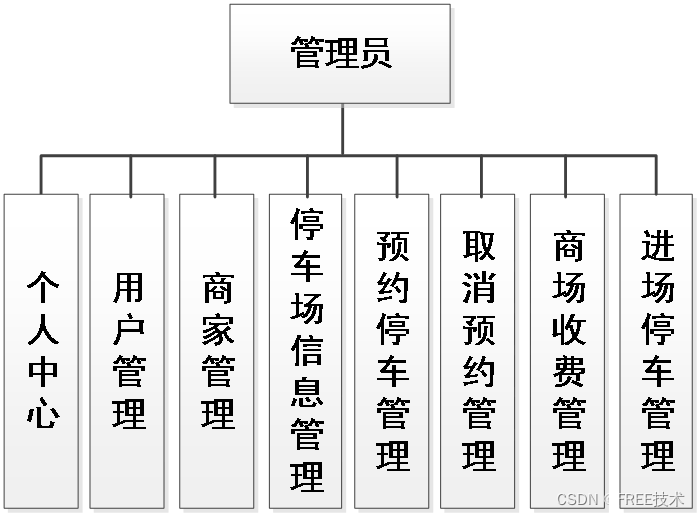
功能截图
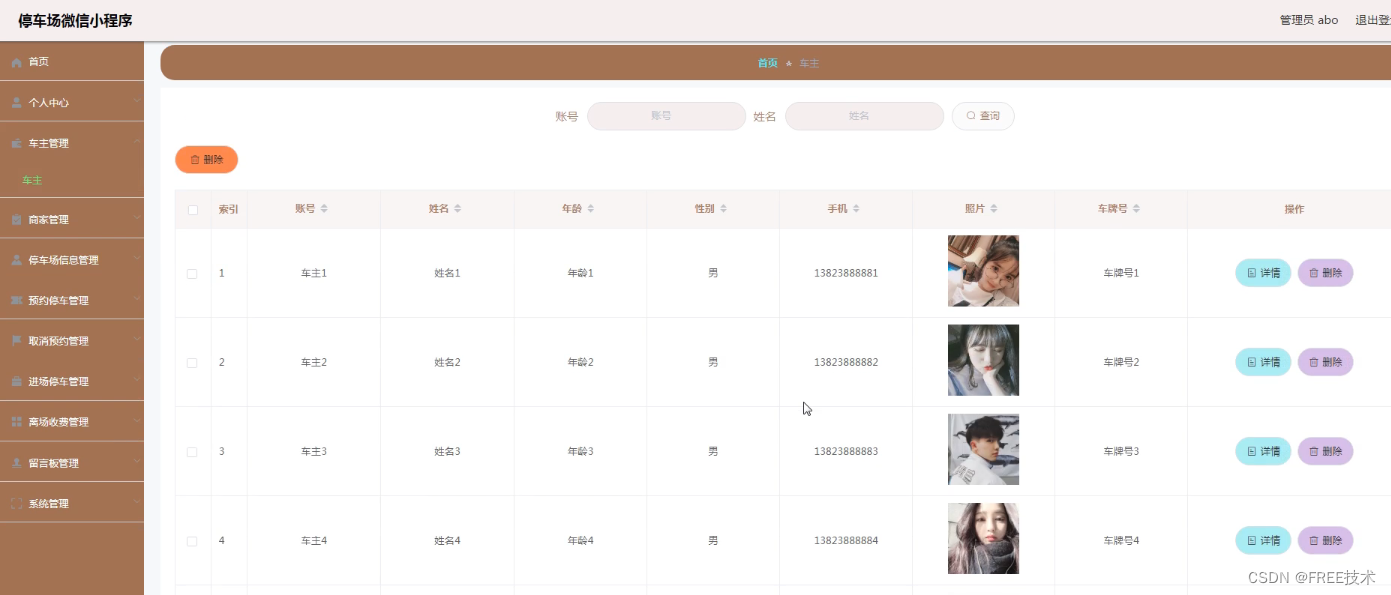
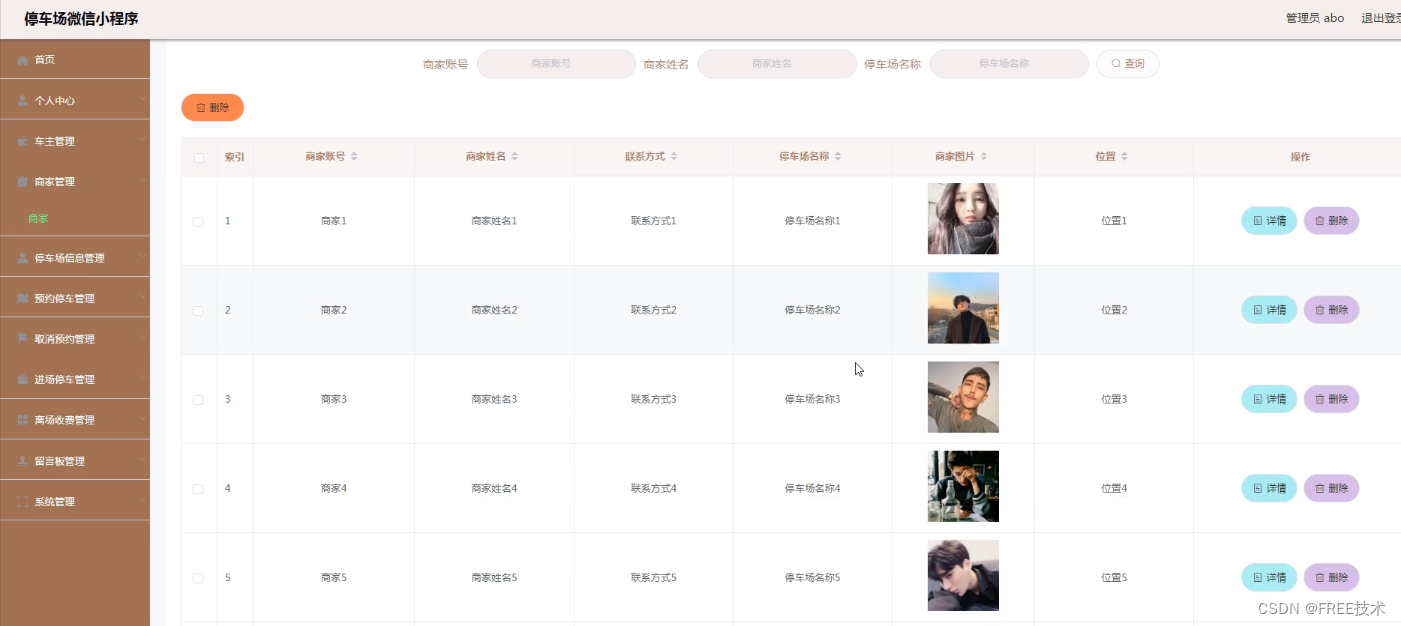
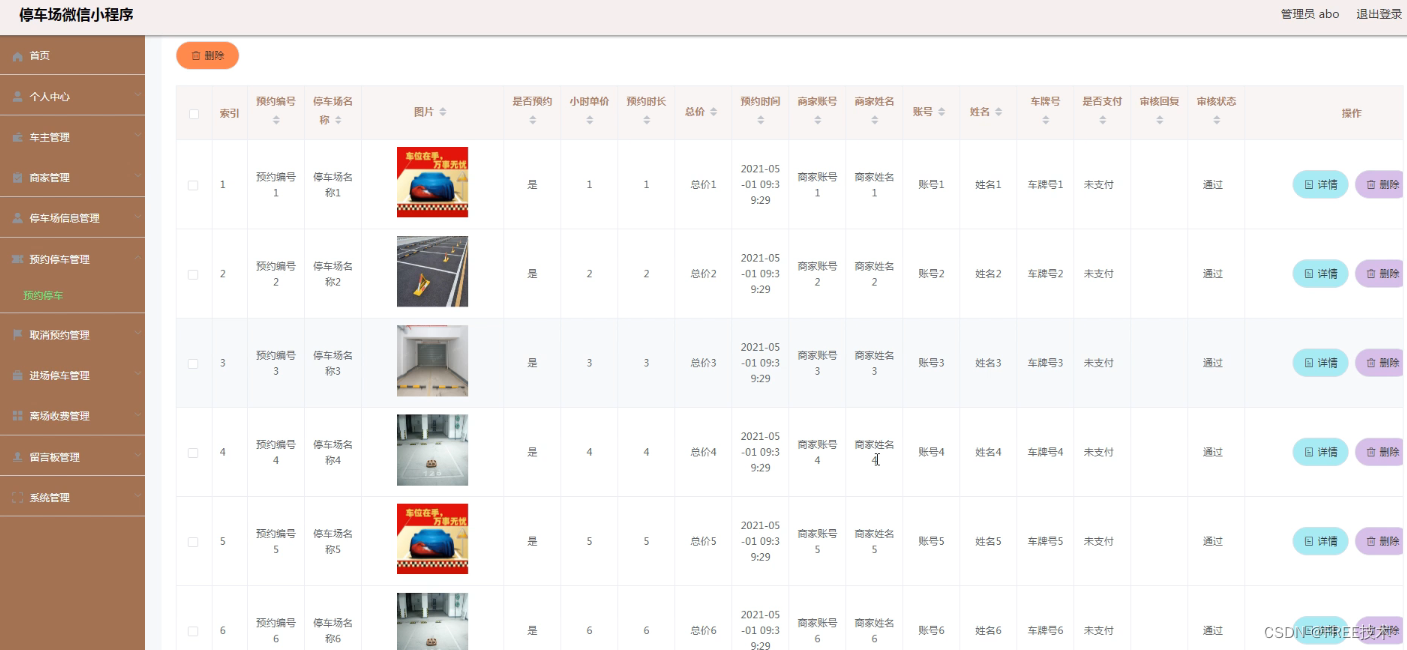
订阅经典源码专栏
Java项目精品实战案例《500套》
源码获取
欢迎大家点赞、收藏、关注、评论啦 。
点击下方卡片获取源码
