与网络公司洽谈做网站需要注意什么企业官网制作报价
ML2023Spring - HW7 相关信息:
课程主页
课程视频
Kaggle link 回来了 : )
Sample code
HW07 视频
HW07 PDF
个人完整代码分享: GitHub | Gitee | GitCode
P.S. HW7 的代码都很易懂,可以和 2024 年的新课:生成式AI导论做一个很好的衔接,因为导论对于 Transformer 库的使用大多数是 HW7 所提到的一些函数。对 AIGC 感兴趣的同学可以去学习,完成 HW7 之后应该能够非常快的上手。
任务目标(抽取式问答)
- 任务描述: 使用 BERT 模型进行抽取式问答。
- 目标: fine-tune BERT 模型,使其能够从文章中抽取出具体答案,完成问答任务。
具体来说,可以当成是预测开始(Start)和结尾(End)的位置,然后抽出这一段作为答案,现在去看PDF中的图你应该更容易理解。
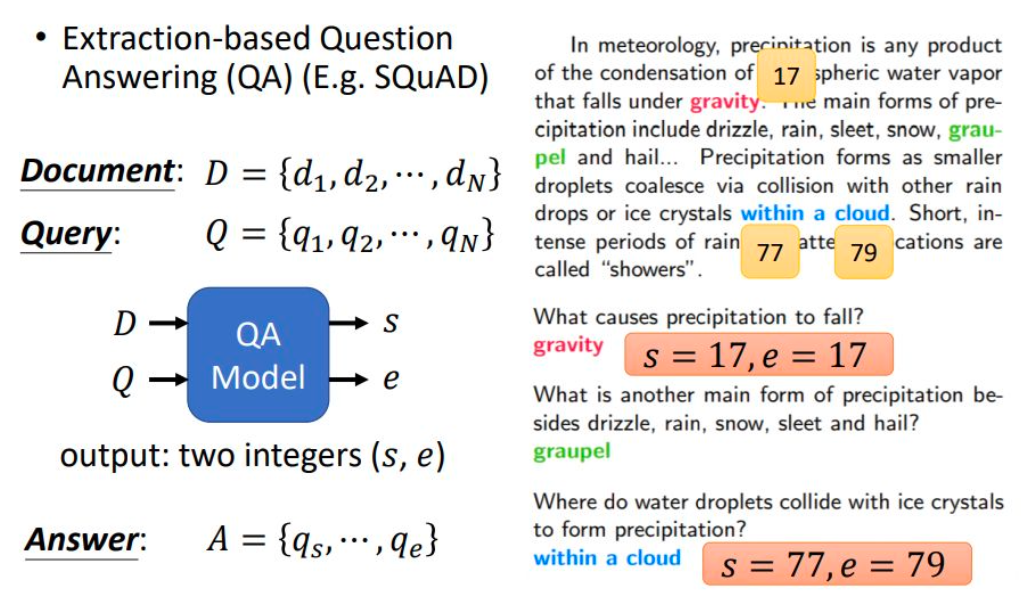
- 目标: fine-tune BERT 模型,使其能够从文章中抽取出具体答案,完成问答任务。
性能指标(EM)
- 准确率 (Exact Match): 该指标用于衡量模型的预测答案与真实答案完全一致的比例。
数据解析
两个繁体中文阅读理解资料集:DRCD 和 ODSQA。
- 训练(DRCD + DRCD-backtrans):包含 15,329 个段落和 26,918 个问题。一个文章段落可能对应多个问题。
- 开发/用于验证(DRCD + DRCD-backtrans):包含 1,255 个段落和 2,863 个问题。
- 测试(DRCD + ODSQA):包含 1,606 个段落和 3,504 个问题。其中段落没有给出答案,需模型进行预测。
训练,开发和测试数据的格式都是相同的:
- id:问题序号
- paragraph_id:文章段落序号
- question_text:问题
- answer_text:答案
- answer_start:答案在文章中的起始点
- answer_end:答案在文章中的终止点

数据下载(kaggle)
To use the Kaggle API, sign up for a Kaggle account at https://www.kaggle.com. Then go to the ‘Account’ tab of your user profile (
https://www.kaggle.com/<username>/account) and select ‘Create API Token’. This will trigger the download ofkaggle.json, a file containing your API credentials. Place this file in the location~/.kaggle/kaggle.json(on Windows in the locationC:\Users\<Windows-username>\.kaggle\kaggle.json- you can check the exact location, sans drive, withecho %HOMEPATH%). You can define a shell environment variableKAGGLE_CONFIG_DIRto change this location to$KAGGLE_CONFIG_DIR/kaggle.json(on Windows it will be%KAGGLE_CONFIG_DIR%\kaggle.json).-- Official Kaggle API
替换<username>为你自己的用户名,https://www.kaggle.com/<username>/account,然后点击 Create New API Token,将下载下来的文件放去应该放的位置:
- Mac 和 Linux 放在
~/.kaggle - Windows 放在
C:\Users\<Windows-username>\.kaggle
pip install kaggle
# 你需要先在 Kaggle -> Account -> Create New API Token 中下载 kaggle.json
# mv kaggle.json ~/.kaggle/kaggle.json
kaggle competitions download -c ml2023spring-hw7
unzip ml2023spring-hw7.zip
不过HW7的数据集比较小,所以我直接上传了 😃,你可以不用自己下载。
Gradescope
Question 1
训练/推理过程的差异
Fine-tuning: 进行梯度下降,调整模型参数。模型通过多个回合(epochs)的训练,学习特定任务的数据集。微调后的模型能够很好地解决特定任务。
In-context learning: 不进行梯度下降,只依赖少量样本,让预训练模型通过上下文提供答案。这是一种轻量的任务特化方式,可以快速得到结果,其实就是 prompt。Label Words are Anchors: An Information Flow Perspective for Understanding In-Context Learning 2023年的这篇文章展示了 In-Context Learning 实际上真的在起作用,如果感兴趣可以阅读原文或者查看24年的视频 第11讲:大型语言模型在「想」什么呢? — 浅谈大型语言模型的可解释性。
拓展阅读:
- Encoder-Only vs Decoder-Only vs Encoder-Decoder Transformer
- Decoder-Only or Encoder-Decoder? Interpreting Language Model as a Regularized Encoder-Decoder
A. Encoder-only 模型(如 BERT 系列)如何在抽取式问答任务中确定答案?
在 BERT 等编码器模型中,抽取式问答的工作原理如下:
-
输入格式:输入由两个部分组成:
- 问题(Question):作为第一个句子(句子 A)。
- 段落(Passage):作为第二个句子(句子 B),其中答案位于该段落中。
-
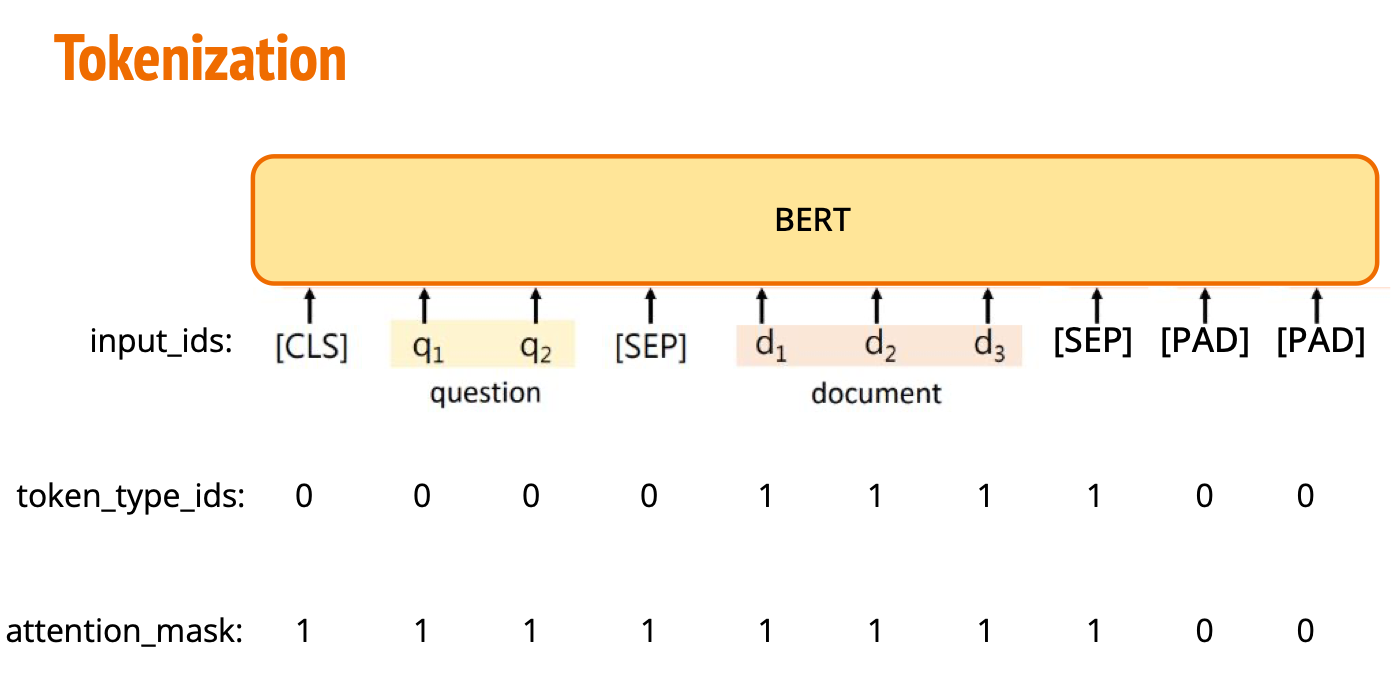
Tokenization(标记化):BERT 对问题和段落进行标记化,并将它们合并成一个输入序列,序列通常是
[CLS] Question [SEP] Passage [SEP]。 -
编码器处理:BERT 对整个输入序列进行处理,生成每个标记的上下文表示。
-
预测开始和结束位置:
-
BERT 通过两个线性层来分别预测答案的起始位置和结束位置。这两个线性层输出每个标记的得分。
# 打印 model 可以看到 qa_outputs。 ... (qa_outputs): Linear(in_features=768, out_features=2, bias=True) -
最终的答案位置是通过找出问题段落中得分最高的开始标记和结束标记的位置来确定。
start_index = torch.argmax(output.start_logits, dim=1) end_index = torch.argmax(output.end_logits, dim=1)
-
-
输出答案:答案是段落中的一段文本,具体由起始位置和结束位置的标记对应的子序列来表示。这些标记会被解码回原始文本,从而得到最终答案。
B. Decoder-only 模型(如 GPT 系列)如何在抽取式问答任务中确定答案?
对于 GPT 等解码器模型,工作原理与 BERT 不同。GPT 生成输出的方式与 BERT 不同,但在处理抽取式问答时也可以通过以下方式确定答案:
-
输入格式:
- GPT 是一个生成式模型,输入格式通常是将问题和段落拼接在一起。例如:
"Question: [问题文本] Passage: [段落文本]"。
- GPT 是一个生成式模型,输入格式通常是将问题和段落拼接在一起。例如:
-
生成式预测:
- GPT 并不是直接输出答案的起始和结束位置。相反,它会根据自回归生成的方式,基于问题生成答案。
- 在抽取式问答任务中,GPT 将段落和问题作为上下文,开始生成答案的第一个标记,并逐步生成后续标记,直到完成生成答案。
-
潜在的问题:由于 GPT 是生成式模型,它可能并不会严格“抽取”段落中的原始文本,而是会生成一个看似合理的答案。它依赖上下文来生成答案,不一定是段落中的原文子串。
-
与 BERT 的差异:GPT 更擅长生成性任务,而不是抽取任务。相比于 BERT 在抽取式问答中的精确性,GPT 更可能生成出看似合理但并不严格匹配原文的答案,也就是瞎编。
总结
- BERT 系列(Encoder-only 模型)会根据标记的上下文表示,直接预测出答案在段落中的起始和结束位置。
- GPT 系列(Decoder-only 模型)通过生成的方式给出答案,基于段落和问题的上下文生成答案,而不是直接定位段落中的子串。
Question 2
尝试不同的 Prompt 并观察 fine-tuning 和 in-context learning 的区别。
这里代码所下载的是 facebook/xglm-1.7B,实际上你也可以直接去 GPT 或者其他 AI 平台问,这里的目的是让你去调整自己的 prompt,从而使模型不经过微调也能获取到正确答案。
Prompt 对比(错误对比)
- Prompt 示例 1: “根据文章找出问题的答案:{问题}”。
- Prompt 示例 2: “请阅读文章并回答以下问题:{问题}”。
- Prompt 示例 3: “请根据文章信息回答下列问题:{问题}”。
Prompt 对比(正确对比)
- 中英对比
- 不同 prompt 对比
代码解析
这里解释一下QA_Dataset,如果觉得太长,可以只查看重点部分。
QA_Dataset 类功能解析(Medium / Strong 相关)
-
初始化(
__init__):split决定数据集的类型(训练、验证或测试)。questions,tokenized_questions, 和tokenized_paragraphs是原问题和 tokenized 后的问题和段落。max_question_len和max_paragraph_len分别设定了问题和段落的最大长度。self.doc_stride:段落的窗口滑动步长(决定每个窗口之间的重叠部分)。Sample code中将其设置为 150,和max_paragraph_len一样,意味着窗口之间完全不重叠。
self.max_seq_len:定义了整个输入序列的最大长度(包含问题和段落)。
-
__getitem__:- 针对给定的索引
idx,获取对应问题和段落数据,返回模型需要的输入。 - 训练集:定位答案的起始和结束位置,将包含答案的段落部分截取为一个窗口(中心在答案位置附近)。然后将问题和段落合并为一个输入序列,并进行填充。
- 验证/测试集:将段落分成多个窗口,每个窗口之间的步长由
self.doc_stride决定,然后将每个窗口作为模型的输入。验证和测试时不需要答案位置,因此只需生成多个窗口作为输入。
- 针对给定的索引
-
填充(
padding):- 输入序列可能比最大序列长度短,填充部分用 0 表示。对于问题部分和段落部分,
token_type_ids被用来区分它们(0 表示问题,1 表示段落)。attention_mask用于标记有效的输入部分,防止模型对填充部分进行注意力计算。
- 输入序列可能比最大序列长度短,填充部分用 0 表示。对于问题部分和段落部分,
重点
self.doc_stride通过控制窗口之间的滑动步长,确保即使答案位于窗口边缘,模型也能通过多个窗口重叠的方式找到答案。- 训练阶段不需要使用
doc_stride,因为训练时我们已经知道答案的位置,可以直接截取包含答案的窗口。但在验证和测试阶段,由于模型并不知道答案的位置,doc_stride保证每个窗口之间有足够的重叠,避免遗漏答案。 - 所以这里存在一个问题,训练过程中模型可能学习到:答案就在中间这一模式。这是我们在 Strong baseline 中需要解决的。
Baselines
论文后遗症上来了,这次会包含多组对比 : ) 每次模块的增加简单基于上次最好的设置进行。
HW7 的代码更多的是在向你演示如何去微调一个能够提取正确答案的 LLM。
括号里是 Kaggle Leaderboard 中的 Public 分数。
Simple baseline (0.45573)
- 运行所给的 sample code。
Medium baseline (0.67820)
-
使用学习率调度器,这里演示两种方法,随意选择即可。
- PyTorch
线性衰减。
from torch.optim.lr_scheduler import LambdaLRtotal_steps = len(train_loader) * num_epochlr_lambda = lambda step: max(0.0, 1.0 - step / total_steps) scheduler = LambdaLR(optimizer, lr_lambda=lr_lambda)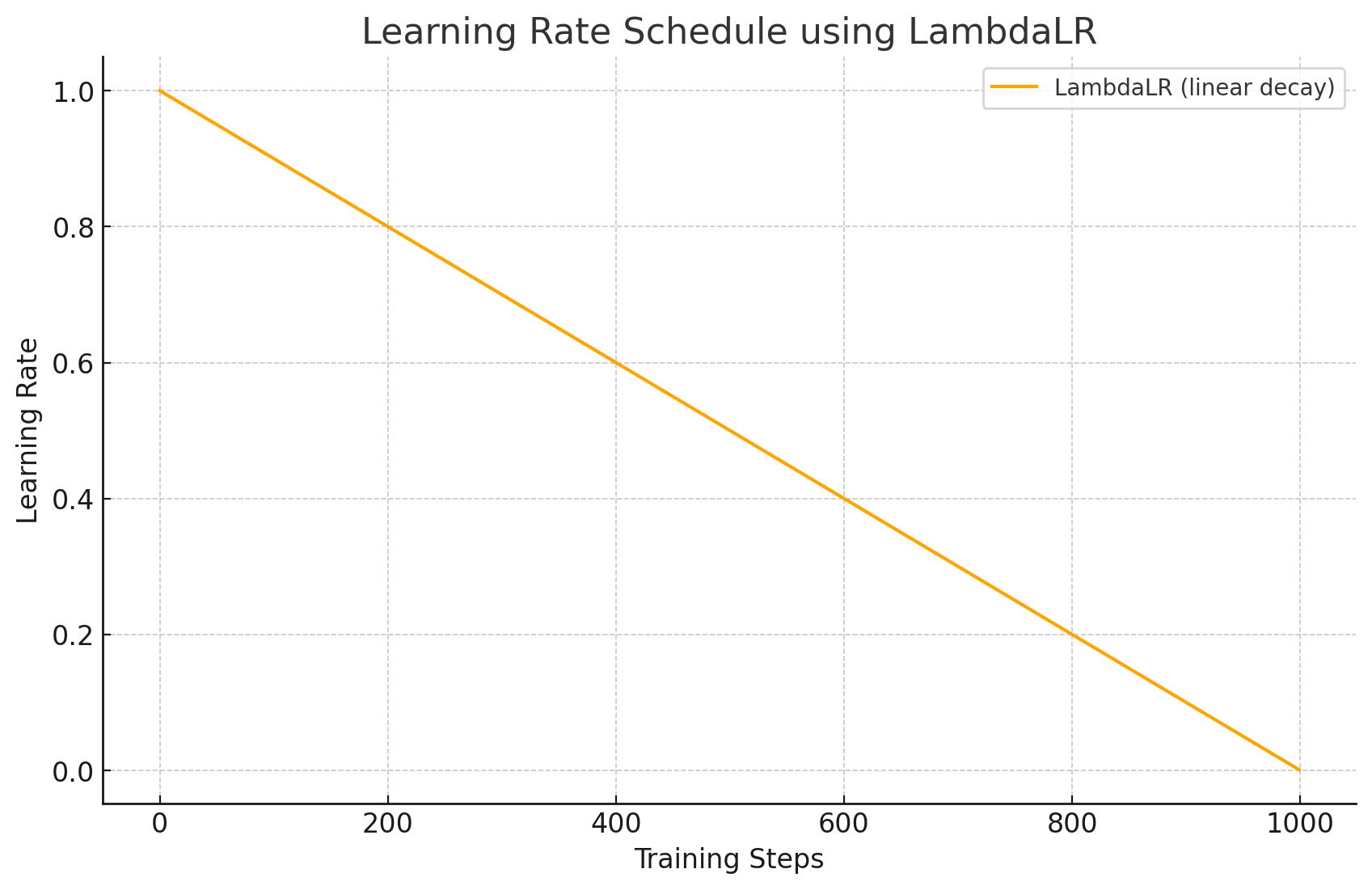
- Hugging Face
使用 warmup。
from transformers import get_linear_schedule_with_warmuptotal_steps = len(train_loader) * num_epoch num_warmup_steps = int(0.2 * total_steps) # 设置为 0 理论上等价于线性衰减,设置为 1 理论上等价于线性增加scheduler = get_linear_schedule_with_warmup(optimizer, num_warmup_steps=num_warmup_steps, num_training_steps=total_steps )不同num_warmup_steps对学习率的影响:

我在当前框架上简单进行了对比(注意,如果你想自己进行对比,请重新运行文件而不是重复运行单元格,不然会导致在之前的模型上继续训练):
Schedule Private Score Public Score no schedule 0.54426 0.56356 Linear schedule (PyTorch) 0.55164 0.56356 Linear schedule with warmup (0) 0.55164 0.56356 Linear schedule with warmup (0.2) 0.54653 0.56356 Linear schedule with warmup (0.5) 0.53916 0.54597 Linear schedule with warmup (1.0) 0.54994 0.55051 这里简单选择Linear schedule with warmup (0)进行下一步实验。
- PyTorch
-
调整
doc_stride参数提升模型表现doc_stride 在 sample code 代码默认为 150,也就是 max_paragraph_len,你可以理解为默认情况下,文本的窗口不重叠,也就是说第一个窗口从 0 开始 149 结束,第二个窗口从 150 开始,299 结束,这两个窗口之间的文本不会发生重叠,但这存在一个问题:问题的答案可能在 140-160 中,默认的设置会无法捕捉到这部分的答案。所以,我们需要调整这个参数,你可以将其理解为段落窗口滑动步长,也可以将其理解为卷积中的 stride。
注意,doc_stride 没有用在训练阶段。
这里给出一些对比,你可以继续实验:
self.doc_stride Private Score Public Score =max_paragraph_len=150 0.55164 0.56356 =max_paragraph_len * 0.75 0.63450 0.62656 =max_paragraph_len * 0.5 0.67366 0.68501 =max_paragraph_len * 0.25 0.70090 0.68161 这里让
self.doc_stride=max_paragraph_len * 0.25进行下一步实验(在你实际实验时应该仅参考 Public Score,因为 Private Score 是最终的批改分数)。
Strong baseline (0.76220)
-
修改模型的预处理过程 (TODO: Preprocessing)
Sample code 对于训练的数据处理是直接以答案为中心选择文本窗口,这导致模型可能学到一个不该学习的模式:答案就在中间。
这里随机偏移答案的窗口位置来解决这一问题,你可以修改 max_offset 的参数:
...# A single window is obtained by slicing the portion of paragraph containing the answermid = (answer_start_token + answer_end_token) // 2# ---- Strong -----# Introduce random offset to prevent learning that answer is always in the middlemax_offset = self.max_paragraph_len # We allow up to 1/4 of the max length as offsetrandom_offset = np.random.randint(-max_offset, max_offset) # Random shift between -max_offset and +max_offset# Adjust paragraph start based on random offsetparagraph_start = max(0, min(mid + random_offset - self.max_paragraph_len // 2, len(tokenized_paragraph) - self.max_paragraph_len))paragraph_end = paragraph_start + self.max_paragraph_len# ---- Strong -----...max_offset Private Score Public Score 不进行偏移 0.70090 0.68161 = self.max_paragraph_len // 4 0.72644 0.72928 = self.max_paragraph_len // 2 0.73155 0.72985 = self.max_paragraph_len 0.72814 0.72701 这里直接选择
self.max_paragraph_len // 2作为偏移进行下一步。
注意,当前代码偏移 > self.max_paragraph_len // 2时并没有确保窗口一定包含答案,所以self.max_paragraph_len偏移效果不佳。 -
选择 HuggingFace 上的其他预训练模型进行微调
在这里找一个模型替换掉当前的:中文模型 – Hugging Face。
Sample code当前使用的是google-bert/bert-base-chinese,一个103M参数的 Fill-Mask 模型,替换模型的话修改下面这行代码即可。
model = AutoModelForQuestionAnswering.from_pretrained("bert-base-chinese").to(device) tokenizer = AutoTokenizer.from_pretrained("bert-base-chinese")Pre-trained Model Params epoch 备注 Private Score Public Score google-bert/bert-base-chinese 103M 1 0.73155 0.72985 2 0.77185 0.75993 google-bert/bert-base-multilingual-cased 179M 1 0.74517 0.74006 2 0.77525 0.76730 FacebookAI/xlm-roberta-base 279M 1 不使用token_type_ids 0.68955 0.67139 NchuNLP/Chinese-Question-Answering 103M 1 不进行训练 0.56299 0.57094 NchuNLP/Chinese-Question-Answering 103M 1 进行训练 0.79001 0.78149
注意:NchuNLP/Chinese-Question-Answering 是一个基于 google-bert/bert-base-chinese 使用 DRCD dataset 进行微调后的问答模型,所以在 kaggle 用的话其实有点降维打击,因为其他模型的 ACC 都是从 0 开始的,而这个模型是从 0.56 开始的,不过可以简单将 epoch 设置高一点自己训练一下 bert-base-chinese,其实没什么差别。
token_type_ids 将输入序列划分为两个部分:
0 表示第一个句子(句子 A),
1 表示第二个句子(句子 B)。
Boss baseline (0.84506)
-
修改后处理部分 (TODO: Postprocessing)
查看 result.csv 文件时,可以发现有些结果是空的。这是因为在某些情况下,预测的结束位置小于开始位置,导致无法捕获到答案文本。我们需要修正这个问题,确保结束位置始终大于或等于开始位置(继续修改 TODO 部分)。
# ---- Boss -----# Ensure the start_index is less than or equal to end_index# This avoids selecting a wrong pair of start and end positionsif start_index <= end_index:# Calculate the combined probability of start and end positionsprob = start_prob + end_prob# If this window has a higher probability answer, update the resultif prob > max_prob:max_prob = prob# Convert token indices to the corresponding text answer# Example: [1920, 7032] --> "大 金"answer = tokenizer.decode(data[0][0][k][start_index : end_index + 1])else:# If start_index > end_index, skip this pair (potentially an error case)continue# ---- Boss -----注意,这部分修改的是 evaluate() 函数,所以不会影响训练,你可以随意的加上自己的想法然后直接运行 Testing 模块得到 result.csv 去查看效果。Boss 增加模块的对比见章末。
-
梯度累积
这是一个非常简单的想法,即不在每次 step 后都更新梯度,这样就等于变相的增加 batchsize,每 n 个 step 更新一次等价于 batchsize 设置为 n*batchsize 。适用于显存不足以跑大 batchsize 的情况。不过 batchsize 大并不意味着效果一定好。
# ---- Boss -----actual_logging_steps = 0 # Track the number of steps contributing to the current logging windowfor batch_idx, data in enumerate(tqdm(train_loader)):# Load all data into GPUdata = [i.to(accelerator.device) for i in data]# Model inputs and forward passoutput = model(input_ids=data[0], token_type_ids=data[1], attention_mask=data[2], start_positions=data[3], end_positions=data[4])# Accumulate lossloss = output.loss / gradient_accumulation_stepsaccelerator.backward(loss)# Update accuracy for the current mini-batchstart_index = torch.argmax(output.start_logits, dim=1)end_index = torch.argmax(output.end_logits, dim=1)batch_acc = ((start_index == data[3]) & (end_index == data[4])).float().mean().item()train_acc += batch_acctrain_loss += loss.item()actual_logging_steps += 1# Gradient accumulation: only update weights every gradient_accumulation_stepsif (batch_idx + 1) % gradient_accumulation_steps == 0:optimizer.step()scheduler.step() # Apply learning rate scheduleroptimizer.zero_grad()step += 1# Loggingif step % logging_step == 0:# Average the loss and accuracy over all accumulated stepsavg_loss = train_loss / actual_logging_stepsavg_acc = train_acc / actual_logging_stepsprint(f"Epoch {epoch + 1} | Step {step} | loss = {avg_loss:.3f}, acc = {avg_acc:.3f}")# Reset the accumulatorstrain_loss = 0.0train_acc = 0.0actual_logging_steps = 0 # Reset after each logging# ---- Boss -----loss = output.loss / gradient_accumulation_steps是因为默认情况下 loss 的计算实际都已经做过平均了,所以我们这里也需要保持一致。另外说一句,其实你也可以直接使用
Accelerator(gradient_accumulation_steps=gradient_accumulation_steps)。 -
训练用上 dev 数据集
去掉验证部分,你需要注意我在这里将QA_Dataset("dev", ...)改为了QA_Dataset("train", ...)dev_set = QA_Dataset("train", dev_questions, dev_questions_tokenized, dev_paragraphs_tokenized) # Boss...combined_train_set = ConcatDataset([train_set, dev_set]) train_loader = DataLoader(combined_dataset, batch_size=train_batch_size, shuffle=True, pin_memory=True) ...# if validation:# print("Evaluating Dev Set ...")# model.eval()# with torch.no_grad():# dev_acc = 0# for i, data in enumerate(tqdm(dev_loader)):# output = model(input_ids=data[0].squeeze(dim=0).to(device), token_type_ids=data[1].squeeze(dim=0).to(device),# attention_mask=data[2].squeeze(dim=0).to(device))# # prediction is correct only if answer text exactly matches# dev_acc += evaluate(data, output) == dev_questions[i]["answer_text"]# print(f"Validation | Epoch {epoch + 1} | acc = {dev_acc / len(dev_loader):.3f}")# model.train()Ensemble 和 early stop 之前我们都在作业中做过,所以不选择这两种方法,直接简单的拼接数据集用于训练看看效果。
简单过一个epoch看看效果(粗体部分就是选择使用的模块):
| epoch | Private Score | Public Score | |
|---|---|---|---|
| - | 1 | 0.79001 | 0.78149 |
| + 修复后处理部分 | 1 | 0.79171 | 0.78263 |
| + 梯度累积(4) | 1 | 0.79171 | 0.79114 |
| 梯度累积(8) | 1 | 0.79057 | 0.78603 |
| 梯度累积(16) | 1 | 0.78376 | 0.77355 |
| + dev数据集 | 1 | 0.79511 | 0.78206 |
现在,我们直接“硬 train 一发”,毕竟该完成的已经完成了,看看最终成效。
作业 PDF 的描述中,Boss 时间是 Simple 的 18.75 倍,加上 dev 数据集后运行时间将增加 12%,所以设置 epochs=16 进行训练查看效果(因为直到 Strong 完成,我们都没有增加参数规模,所以当前训练时间等于 Simple)。
最终的结果(epoch=16):
- Public Score:0.79114
- Private Score:0.77525
虽然在训练集的结果上,第 16 个 epoch 比第 1 个 epoch 的 ACC 高了 0.073,但实际上,这是过拟合的,Kaggle 的最终提交结果甚至不如只训练 1 次的情况。(到这里其实就足够了,你已经学到了这份作业想要教你的知识,后面会是一些预训练模型的结果分享,或许能够帮你节省一些时间)。
所以,让我们换一个更大的模型 : )
| Pre-trained Model | Params | epoch | Private Score | Public Score |
|---|---|---|---|---|
| DaydreamerF/chinese-macbert-base-finetuned-accelerate | 101M | 2 | 0.78830 | 0.78660 |
| IDEA-CCNL/Erlangshen-MacBERT-325M-TextMatch-Chinese | 324M | 2 | 0.78887 | 0.79228 |
| hfl/chinese-macbert-large | 324M | 1 | 0.81668 | 0.82349 |
| 5 | 0.83144 | 0.83030 | ||
| luhua/chinese_pretrain_mrc_macbert_large | 324M | 1 | 0.83654 | 0.82292 |
| 2 | 0.84222 | 0.83144 | ||
| 2 (FP32) | 0.84165 | 0.82973 | ||
| 3 | 0.83777 | 0.82065 | ||
| 5 | 0.82917 | 0.82463 | ||
| qalover/chinese-pert-large-open-domain-mrc | 324M | 0 | 0.56413 | 0.54143 |
| 2 | 0.83314 | 0.82519 |
在导入大模型的时候你可能会遇到显存不够的情况,这时候降低 train_batch_size 增加gradient_accumulation_steps 就可以了。
#train_batch_size = 8
#gradient_accumulation_steps = 4train_batch_size = 4
gradient_accumulation_steps = 8
如果想在 2 个 epoch 下达到 Boss baseline,可以寻找并选择大于 324M 的预训练模型。
最后补充一个 doc_string 的对比,doc_string 也是后处理的模块,下面的结果基于 luhua/chinese_pretrain_mrc_macbert_large 在 epoch=2 下进行修改。
| doc_string | Private Score | Public Score |
|---|---|---|
| =max_paragraph_len*0.25 | 0.84222 | 0.83144 |
| =max_paragraph_len*0.1 | 0.84335 | 0.83087 |
| =max_paragraph_len*0.05 | 0.83881 | 0.82746 |
至此,Homework7 就结束了,希望能对你有所帮助。
拓展链接
-
Encoder-Only vs Decoder-Only vs Encoder-Decoder Transformer
-
Decoder-Only or Encoder-Decoder? Interpreting Language Model as a Regularized Encoder-Decoder
-
中文模型 – Hugging Face
-
Gradient Accumulation in PyTorch
进一步
我将 24 年的课程作业修改为了大陆可以访问的 API,并攥写了所有作业的中文引导和代码镜像,你可以在这里快速索引:
李宏毅2024生成式人工智能导论 中文镜像版指导与作业