公司部门岗位职责宁波seo推广费用
概述
计算机网络是指将地理位置不同的具有独立功能的多台计算机及其外部设备,通过通信线路连接起来,在网络操作系统、网络管理软件及网络通信协议的管理和协调下,实现资源共享和信息传递
网络分类
- 局域网(LAN)
- 局域网是一种在小区域内使用的,由多台计算机组成的网络,覆盖范围通常局限在10千米范围之内,属于一个公司或部门组建的小范围区域
- 城域网(MAN)
- 城域网是作用范围在广域网与局域网之间的网络,其网络覆盖范围通常可以延伸到整个城市,借助通信光纤将多个局域网联通公用城市网络形成大型网络,使得不仅局域网内的资源可以共享,局域网之间的资源也可以共享
- 广域网(WAN)
- 广城网是一种远程网,涉及长距离的通信,覆盖范围可以是多个国家甚至整个世界。由于广域网地理上的距离过于长,所以信息衰减非常严重,这种网络一般要租用专线,通过接口信息处理协议和线路连接起来,构成网状结构,解决寻径问题
网络通信协议

计算机网络中实现通信必须有一些约定,即通信协议。包括对速率、传输代码、代码结构、传输控制步骤、出错控制等制定的标准。常见的网络通信协议有:TCP/IP协议、IPX/SPX协议等。为了使两个节点之间能进行对话,必须在他们之间建立通信工具(即端口port),使彼此之间能进行信息交换。
TCP/IP协议:传输控制协议/因特网互联协议(Transmission Control Protocol/Internet Protocol),是Internet最基本、最广泛的协议。它定义了计算机如何连入因特网,以及数据如何在它们之间传输的标准。它的内部包含一系列的用于处理数据通信的协议,并采用了4层的分层模型,每一层都呼叫它的下一层所提供的协议来完成自己的需求。
- 应用层:主要负责应用程序的协议,例如HTTP协议、FTP协议等。
- 传输层:主要使网络程序进行通信,在进行网络通信时,可以采用TCP协议,也可以采用UDP协议。
- 网络层:网络层是整个TCP/IP协议的核心,它主要用于将传输的数据进行分组,将分组数据发送到目标计算机或者网络。
- 数据链路层:链路层是用于定义物理传输通道,通常是对某些网络连接设备的驱动协议,例如针对光纤、网线提供的驱动
TCP
传输控制协议(Transmission Control Protocol),TCP协议是面向连接的通信协议,即在传输数据之前发送端和接收端建立逻辑连接,然后进行传输数据,它提供了两台计算机之间可靠无差错的数据传输;在TCP连接中必须要明确客户端与服务器端,由客户端向服务端发出连接请求,每次连接的创建都需要经过“三次握手”,TCP的客户端和服务端断开连接时候需要四次挥手
三次握手
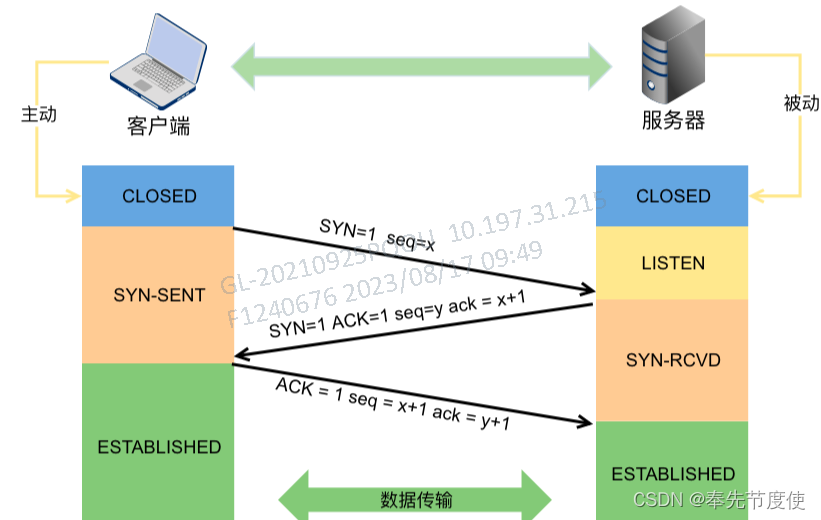
- 第一次握手:客户端发送SYN(SEQ=x)报文给服务器端,进入SYN_SEND状态。(客户端向服务器端发出连接请求,等待服务器确认)
- 第二次握手:服务器端收到SYN报文,回应一个SYN (SEQ=y)ACK(ACK=x+1)报文,进入SYN_RECV状态(服务器端向客户端回送一个响应,通知客户端收到了连接请求)
- 第三次握手:客户端收到服务器端的SYN报文,回应一个ACK(ACK=y+1)报文,进入Established状态(客户端再次向服务器端发送确认信息,确认连接)
三次握手结束,TCP客户端和服务器端成功地建立连接,接下来可以开始传输数据~
四次挥手
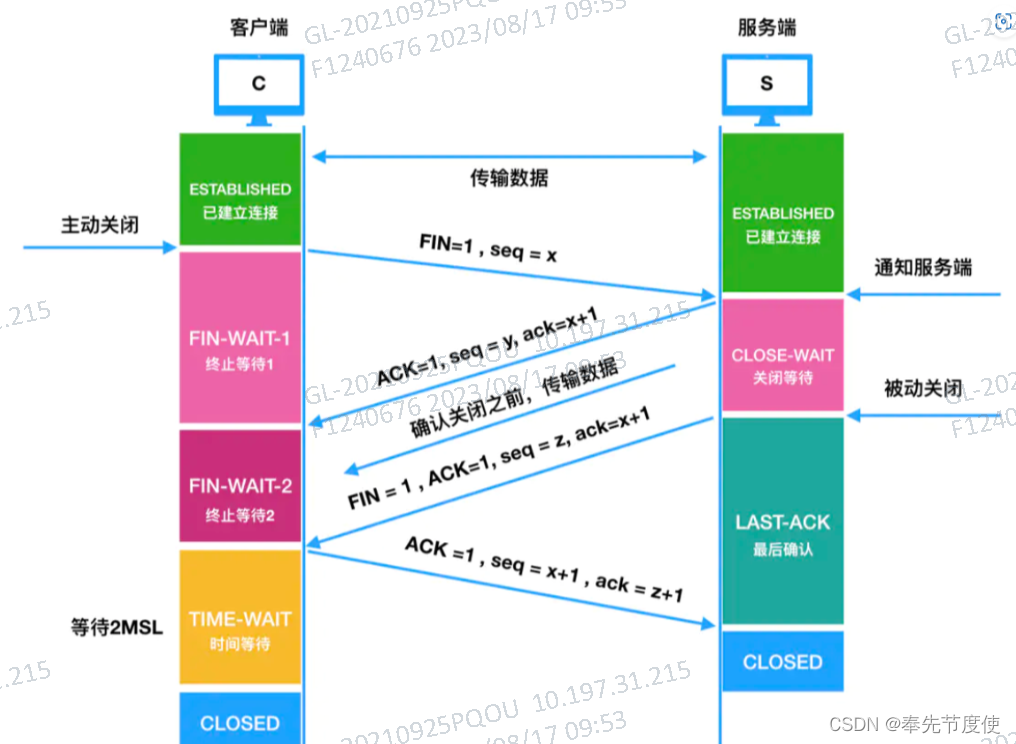
- 客户端打算关闭连接,此时会发送一个TCP首部FIN标志位被置为1的报文,即FIN报文,之后客户端进入FIN_WAIT_1状态
- 服务端收到该报文后,就向客户端发送ACK应答报文,接着服务端进入CLOSED_WAIT状态
- 客户端收到服务端的ACK应答报文后,之后进入FIN_WAIT_2状态
- 等待服务端处理完数据后,也向客户端发送FIN报文,之后服务端进入LAST_ACK状态
- 客户端收到服务端的FIN报文后,回一个ACK应答报文,之后进入TIME_WAIT状态
- 服务器收到了ACK应答报文后,就进入了CLOSE状态,至此服务端已经完成连接的关闭
- 客户端在经过2MSL一段时间后,自动进入CLOSE状态,至此客户端也完成连接的关闭
由上图可以知道,每个方向都要有一个FIN和一个ACK,因此通常被称为四次挥手。这一点注意:主动关闭连接的,才可进入TIME_WAIT状态
UDP
- 用户数据报协议(User Datagram Protocol)(数据报(Datagram)是UDP网络传输的基本单位)
- UDP是无连接通信协议,即在数据传输时数据的发送端和接收端不建立逻辑连接。即当一台计算机向另外一台计算机发送数据时,发送端不会确认接收端是否存在就会发出数据,同样接收端在收到数据时,也不会向发送端反馈是否收到数据。
- 由于使用UDP协议消耗资源小,通信效率高,所以通常都会用于音频、视频和普通数据的传输例如视频会议都使用UDP协议,因为这种情况即使偶尔丢失一两个数据包,也不会对接收结果产生太大影响。
- 但是在使用UDP协议传送数据时,由于UDP的面向无连接性,不能保证数据的完整性,因此在传输重要数据时,不建议使用UDP协议
IP协议
概念
IP协议(Internet Protocol)又称互联网协议,是支持网间互联的数据包协议。该协议工作在网络层,主要目的就是为了提高网络的可扩展性,与传输层TCP相比,IP协议提供一种无连接/不可靠、尽力而为的数据包传输服务,其与TCP协(传输控制协议)一起构成了TCP/IP协议族的核心
分类
- IPv4:为每个连接在网络上的主机分配一个32bit地址。按照TCP/IP规定,IP地址用二进制来表示且每个IP地址长32bit,即4个字节;为了方便使用IP地址采用点分十进制,如“192.168.1.66”
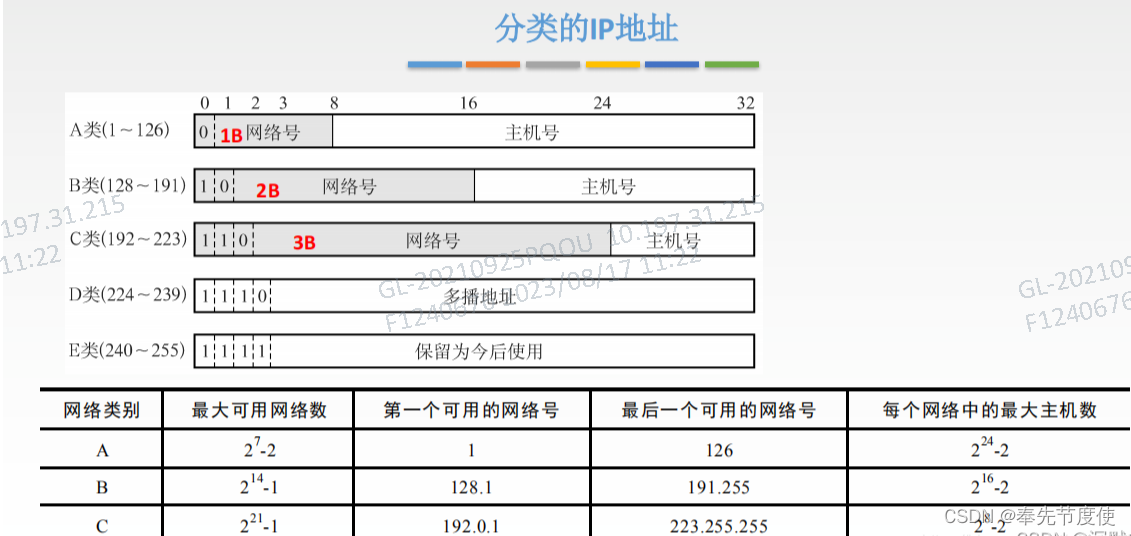
-
IPv6: 由于互联网的蓬勃发展,IP地址的需求量越来越多,为了扩大地址空间,通过IPv6采用128位地址长度定义地址,这样就解决了网络地址资源数量不够的问题
-
常用命令: ① ipconfig:查看本机 IP 地址(Linux下对应ifconfig) ② ping IP 地址:检查网络是否连通。
