安徽海鹏建设工程有限公司网站六安网站制作
web 基础
网上冲浪
就是在互联网(internet)上获取各种信息,进行工作,或者娱乐,他的英文表示surfing the Internet,因 “surfing”d的意思是冲浪,即成为网上冲浪,这是一种形象说法, 也是一个非常有历史意义的词汇。
t.cn 是微博的一个短域名 https://weibo.com/ weibo.com 域名 主机名 微博服务器的地址名
当用户在地址栏输入了一个URL(uniform resource locator 统一资源定位符)常见的URL
# 常见的URL 网站域名 luffycity.com baidu.com weibo.com taobao.com 产品名称:L4150 Series 出厂编号:X4DK078422 https://myepson.epson.com.cn/epmtoc/pcfrontend/web/login/index
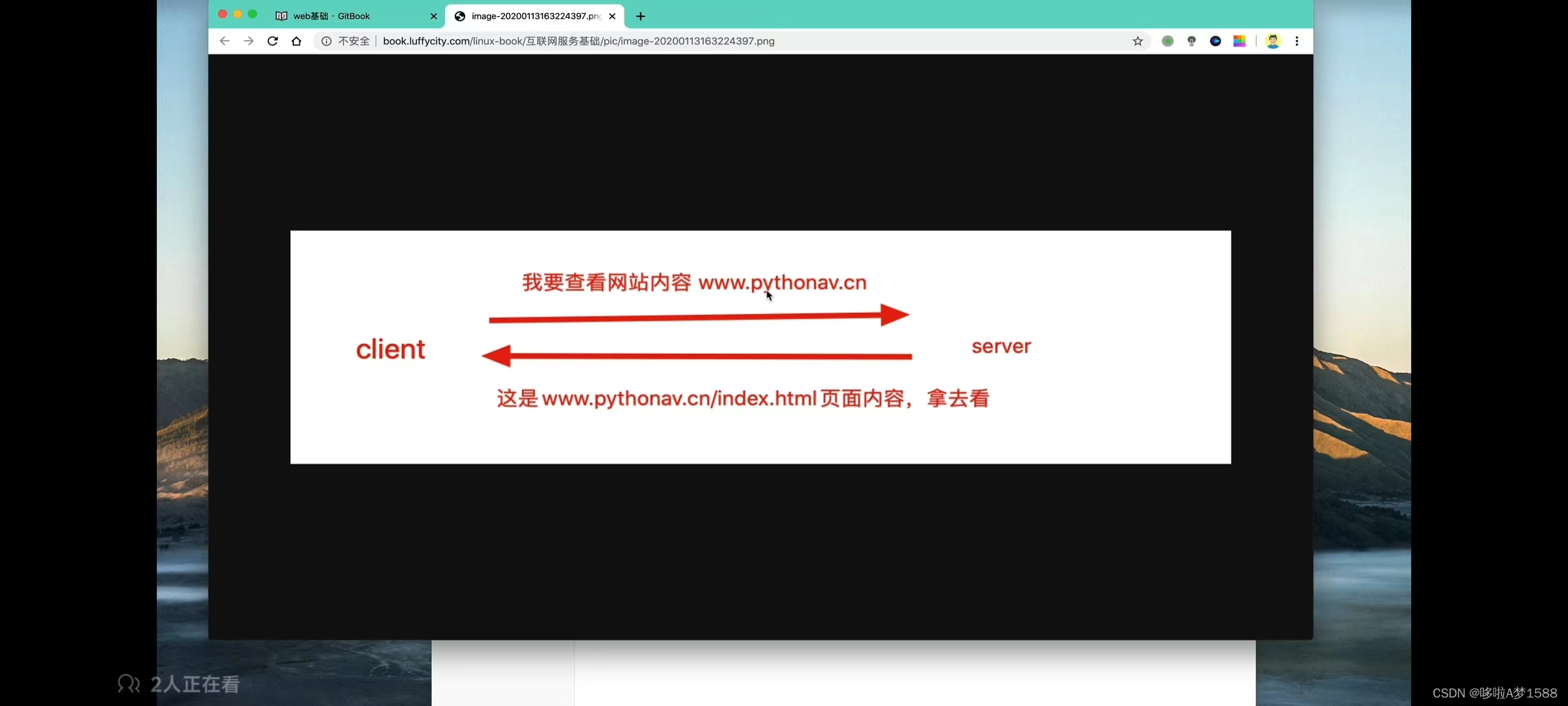
浏览器向这个域名的服务器发送了请求,我要看你的网站内容
浏览器就会根据用户输入的域名,进行域名解析(baidu.com解析成服务器的IP地址)向该服务器所运行的一个(web server服务器程序)这个web服务器软件能够在机器上寻找用户想要的资料,最终返回给用户,浏览器进行渲染。
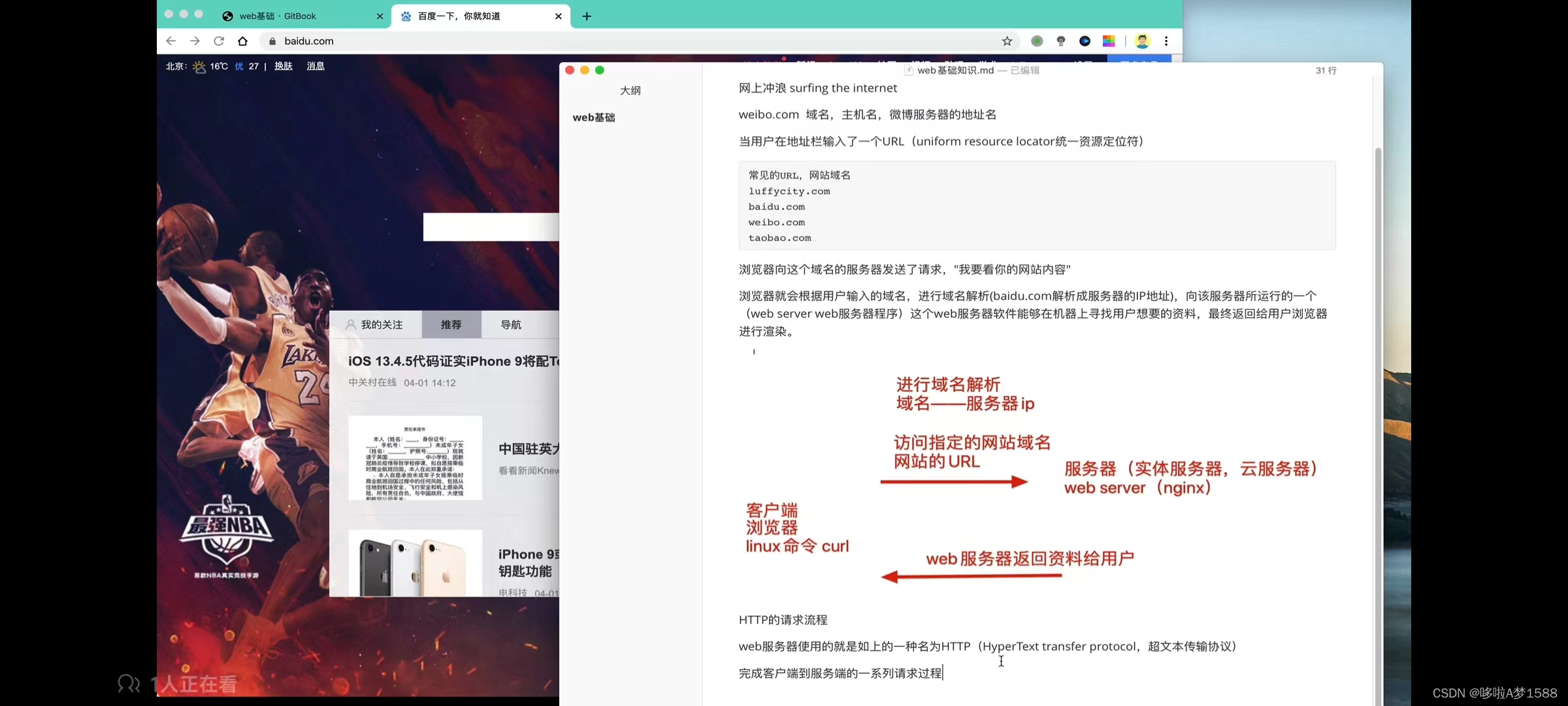
HTTP的请求流程
web服务器使用的就是如上的一种名为HTTP (HyperText transfer protocol,超文本传输协议)
完成客户端到服务端的一系列请求过程

TCP/IP协议
通常互联网就是以 TCP/IP 协议去运转的,我们上面所说的HTTP的请求流程,它也是 tcp/ip 的一个子集,
我们以前学的 OSI体系
1. 物理层:指的是硬件设备
2. 数据链路层:网卡对应的一个 mac 地址,
3. 网络层:
4. 运输层
5. 会话层
6. 表示层
7. 应用层
网卡对应的一个 mac 地址,厂家在出厂时打的标号,是你这个电脑在世界上的唯一地址,通过网卡,就可以给电脑插上网线,给它分配一个 IP 地址,通过网络层,传输层,给他进行 IP 传输,最终我们通过 IP 地址和一个软件进行通信,比如我在客户端电脑上,在应用层(指的是安装的各种各样的软件 浏览器) 通过浏览器发送HTTP请求,从我这台电脑的 IP 地址,然后经过 mac地址,经过这条机器的网卡,最终通过互联网和其他人进行通信。
计算机要和网络设备进行通信,比如你的笔记本和你们家的路由器,从路由器出去和公网进行交互,双方就得基于一个同样的方法,同样的协议,你如何探测到目标机器,是由哪一方先发起通信过程的,是谁先找谁,找到之后然后进行交流呢?交流完后又如何进行结束呢?这些规则都是需要事先定义的。不同的硬件,不同的操作系统之间他们的沟通方式都是不一样的。这一切都要定制一个统一的规则。这个规则我们称之为 Protocol 协议
Protocol 协议 :
比如中国人说中文,美国人说 英文,一个中国人和一个美国人如何交流,是不是要有一套标准,要么都说中文,要么都说英文,两个人要达成协议,才能进行沟通交流,即通信。
协议存在各种各样的形式,常见的协议如下:
-
icmp 协议,全称 Internet control message protocol 用于在服务器之间,网络设备之间进行消息传递,询问。
-
dns 协议 建立在 UDP 和TCP 协议之上,默认使用服务器的 53 端口进行通信。主要是用来域名解析,能够把主机名(域名)解析成为一个 IP 地址
-
FTP 协议,file transfer protocol 文件传输协议,主要是两部分:client 和 server FTP服务器用来存储数据的
-
nfs协议,rpc协议+nfs 协议 运行处理网络共享文件系统 网络文件系统,它是在 linux 系统之间传输的协议
-
snmp, 应用层协议 能够让系统管理员或者说网络管理员高效的去管理网络问题以及进行网络划分,能够预先告警,发现网络设备的问题 主要用于管理网络节点之上,能够管理服务器,路由器,交换机等
-
http 协议,它是一个简单的请求,响应的协议 运行在 TCP/IP 协议之上,指定了客户端能够给服务器发送什么形式的请求 我们要重点掌握的协议
数据包中转
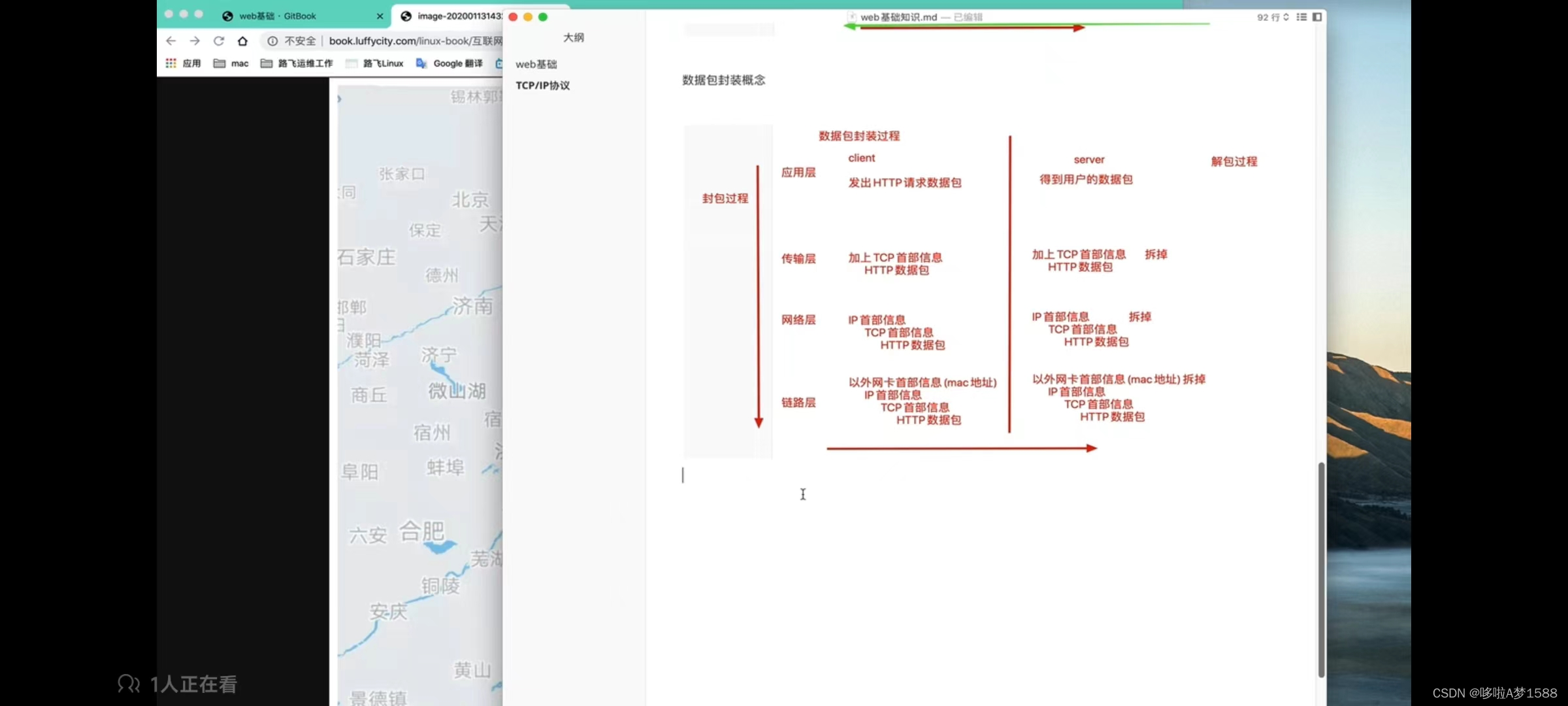
1. 客户端发起一个 HTTP请求 (访问一个页面)
2. TCP/IP 协议为了传输方便,在TCP传输层,将请求报文分割,且在每个报文上打上标记,转发给网络层
3. 网络层再增加一个标记,目标机器的MAC地址发给链路层,这时候,网卡就知道数据发给谁了
4. 接受者在链路层接收到数据,向上走,最终到应用层(web nginx)
IP 协议
全称为 Internet protocol, IP 协议 处于网络层中
IP 协议 的作用是,把数据包发送到指定的目的地,这里最重要的就是 IP 地址和 MAC 地址,
IP 地址:是指定了服务器在网络中的一个地址信息 属于网络层 IP地址他依赖于 MAC 地址 ,局域网通信还是很少的
MAC 地址:是指服务器网卡硬件设备的设备号 (机器在出厂的时候,就设置好的,全球唯一的MAC地址号) 属于物理链路层
IP 和 ARP 的关系
ARP 协议就是把 IP地址和MAC地址进行解析的一个协议
网络数据包的传递过程,好比是快递中转站的过程
小明
http://123.206.16.61/chaoge.jpg
把该请求转发给路由器,第一个中转站:
转发给一个中转站
中转站的设备MAC地址
00-xx-c1-b1-xx-xx这是网络相关的概念,用户的请求并不是一条直线,直达目的地,而是通过很多中转站(n 多个路由设备,挨个转发)他会先到第一个中转站,进入到下一个中转站: 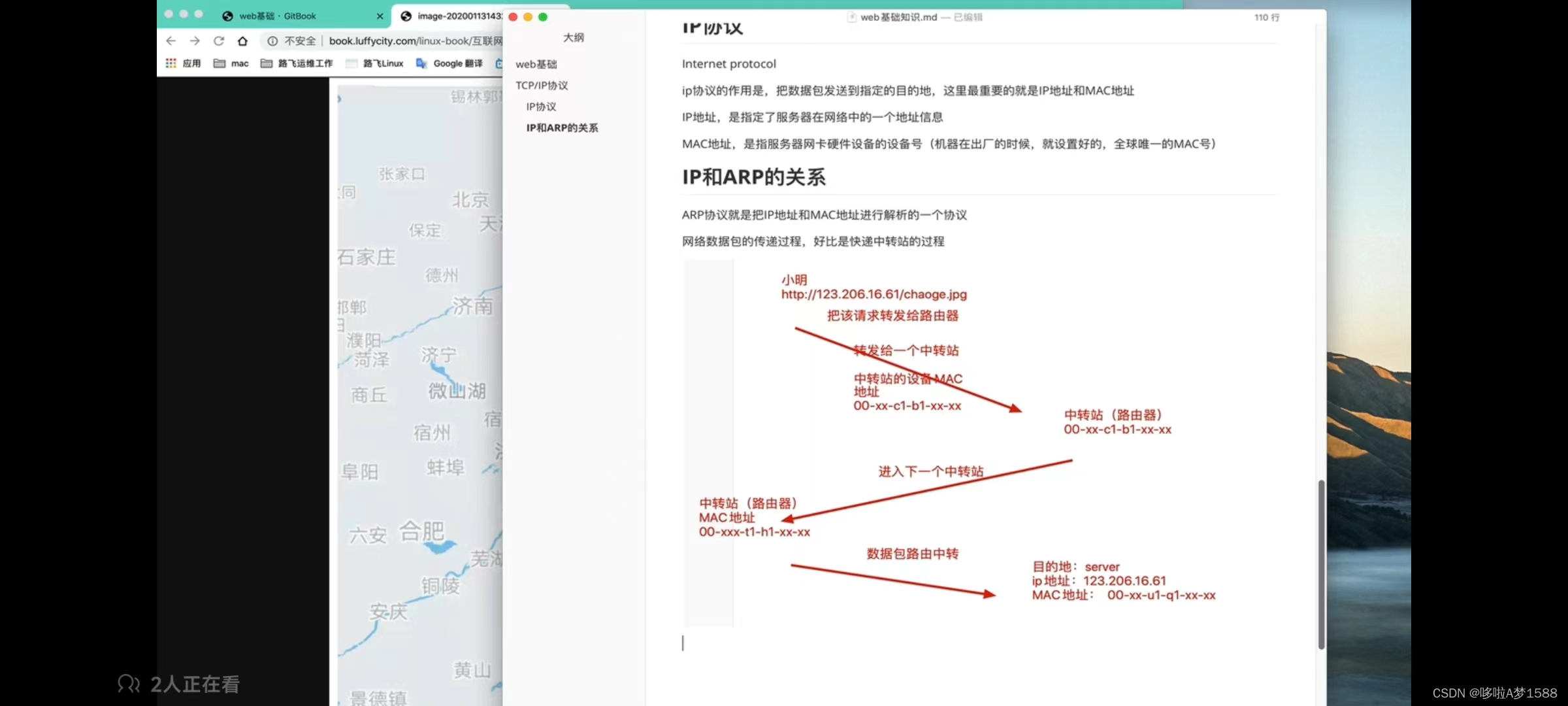
TCP协议
TCP协议位于传输层,提供可靠的字节流服务 (Byte Stream Service),指的是以字节流的形式传递给接收者,没有固定的报文边界限制,只能知道总共发送的数据,但是不知道一次能读取多少数据,为了更容易传输大数据将数据切割了。
三次握手
syn 表示建立连接的信号
ack 确认消息
seq 序列号
rcvd 收到
established 已建立连接
为了数据传输的准确性,服务端和客户端之间需要三次的交互(三次握手)
-
第一次,client 发送 syn 包 (syn=j) 给 server,进入 SYN_SEND状态,等待服务器确认
-
第二次,server 收到 syn 包,确认 client 发来的 syn (ack=j+1),同时自己发送一个 SYN包 (syn=k), 也就是 SYN+ACK 包,此时 server 进入 SYN_RECV状态
-
第三次,客户端接收到服务器的 SYN+ACK 包,向服务器发送确认包 ACK(ack=k+1), 此时包发送完毕了,客户端和服务器进入 ESTABLISHED 状态,完成三次握手。


大白话解释三次握手:
第一次握手:客户端发送了 SYN=1,seq=x ,这个x是一个随机数,服务端接收到了客户端发来的数据包,知道自己要和客户端建立连接了;
第二次握手:服务器给客户端发送一个 SYN=1,seq=y 随机数,ACK=x+1,服务器发送前两个数据都是为了证明自己的发消息的能力,服务器在客户端发出的seq随机数上+1是表示明确客户端身份,他俩是同一个连接。
第三次握手:客户端再次向服务器发送一个ACK=Y+1,明确告诉服务器,可以和客户端进行通信了。
DNS协议

如何去搭建一个网站?以及让这个网站支持高可用的集群,以及能够支持一个高性能的并发,我们学习了这么多 linux 命令,我们会带着大家,比如说,一个网站,怎么把这个网站搭建出来,以及涉及它的域名,端口,以及我们能够让这个网站动态资源,静态资源,进行一个高性能的处理网站,可以展示图片,文字以及视频,登录以后才可以看到视频,它可以看到静态的内容,也可以看到动态的内容,比如购物车的数据啦,登录注册等等,问题来了,我们怎么去搭建这些服务呢?我们需要掌握 web 服务的基础知识。HTTP
http:hyper text transfer protocol
HTTP 协议用于 client 和 server 之间通信,一般是请求一个静态资源称之为客户端,提供资源的一方称之为服务端
URL 与 URI
URI包括URL和URN两个类别,URL是URI的子集,所以URL一定是URI,而URI不一定是URL
URI = Universal Resource Identifier 统一资源标志符,用来标识抽象或物理资源的一个紧凑字符串。
URL = Universal Resource Locator 统一资源定位符,一种定位资源的主要访问机制的字符串,一个标准的URL必须包括:protocol、host、port、path、parameter、anchor。
URN = Universal Resource Name 统一资源名称,通过特定命名空间中的唯一名称或ID来标识资源。
在这里插入图片描述
举个栗子
个人的身份证号就是URN,个人的家庭地址就是URL,URN可以唯一标识一个人,而URL可以告诉邮递员怎么把货送到你手里。
举个栗子
https://blog.csdn.net/GTQ28是个URL,通过这个网址可以告诉CDN找到我的博客所在地,并且还告诉用HTTP协议访问。
详细说明
一、URI详细说明
一、URI
<1>什么是URI
URI,统一资源标志符(Uniform Resource Identifier, URI),表示的是web上每一种可用的资源,如
HTML文档、图像、视频片段、程序等都由一个URI进行标识的。
<2>URI的结构组成
URI通常由三部分组成:
①资源的命名机制;
②存放资源的主机名;
③资源自身的名称。
(注意:这只是一般URI资源的命名方式,只要是可以唯一标识资源的都被称为URI,上面三条合在一起是URI的充分不必要条件)
二、URL
URL是URI的一个子集。它是Uniform Resource Locator的缩写,译为“统一资源定位 符”。
通俗地说,URL是Internet上描述信息资源的字符串,主要用在各种WWW客户程序和服务器程序上。
采用URL可以用一种统一的格式来描述各种信息资源,包括文件、服务器的地址和目录等。URL是URI概念的一种实现方式。
URL的一般格式为(带方括号[]的为可选项):
protocol : // hostname[:port] / path / ;parameters#fragment
URL的格式由三部分组成:
①第一部分是协议(或称为服务方式)。
②第二部分是存有该资源的主机IP地址(有时也包括端口号)。
③第三部分是主机资源的具体地址,如目录和文件名等。
第一部分和第二部分用“: //”符号隔开,
第二部分和第三部分用“/”符号隔开。
第一部分和第二部分是不可缺少的,第三部分有时可以省略。
<3>URL举例
如:https://blog.csdn.net/GTQ28
我们可以这样解释它:
①这是一个可以通过https协议访问的资源,
②位于主机 blog.csdn.net上,
③通过“GTQ28”可以对该资源进行唯一标识(注意,这个不一定是完整的路径)
三、URI和URL之间的区别
从上面的例子来看,你可能觉得URI和URL可能是相同的概念,其实并不是,URI和URL都定义了资源是什么,但URL还定义了该如何访问资源。URL是一种具体的URI,它是URI的一个子集,它不仅唯一标识资源,而且还提供了定位该资源的信息。URI是一种语义上的抽象概念,可以是绝对的,也可以是相对的,而URL则必须提供足够的信息来定位,是绝对的。
四、通俗说
统一资源标志符URI就是在某一规则下能把一个资源独一无二地标识出来。
拿人做例子,假设这个世界上所有人的名字都不能重复,那么名字就是URI的一个实例,通过名字这个字符串就可以标识出唯一的一个人。现实当中名字当然是会重复的,所以身份证号才是URI,通过身份证号能让我们能且仅能确定一个人。
那统一资源定位符URL是什么呢。也拿人做例子然后跟HTTP的URL做类比,
就可以有:动物住址协议://地球/中国/浙江省/杭州市/西湖区/某大学/14号宿舍楼/525号寝/张三.人
可以看到,这个字符串同样标识出了唯一的一个人,起到了URI的作用,所以URL是URI的子集。URL是以描述人的位置来唯一确定一个人的。
URI (Uniform Resource Identifiler)
uri 中文叫"统一资源标识符",是一个用于标识某一互联网资源名称的字符串,在世界互联网范围内标识定位某一个唯一信息资源。
例如
# 访问一张郭达的照片 http://www.pythonay.cn:80/man.jpg http://www.pythonay.cn/guoda.gif http://www.pythonay.cn/index.html https://www.luffycity.com/home
URL(Uniform Resource Locator)
url 主要用在各种 www 客户端和服务器程序上,url 可以用一种统一的格式来描述各种信息资源,包括图片,视频,txt文件,html文件,服务器地址和目录等
【url组成】
1. 协议 # 比如 http:// 协议
2. 主机ip 或域名 # pythonay.cn ,通过dns的解析成服务器的ip地址
3. 端口 # 80 是http的默认端口 443是加密的http协议,也加https协议
4. 文件资源具体地址
# home(在服务器是具体什么位置,通过 web 服务器配置修改的)
5.
第一部分用 "://" 隔开,第二部分用 "/" 符号隔开
HTML
超文本标记语言(英语:HyperText Markup Language, 简称 :HTML) 是一种用于创建网页的标准标记语言。
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>chaoge.linux</title>
</head>
<body><h1>我的第一个标题</h1><p>我的第一个段落。</p>
</body>
</html>获取html源码的方式
1) curl www.pythonay.cn
可以重定向到
curl pythonay.cn > ./pythonay.html
vim pythonay.html 也可以看到源代码
2) 浏览器检查网页源码CSS
css指层叠样式表(Cascading Style Sheets)
css作用是定义如何显示HTML元素样式
HTML HTML+CSS
JS
JavaScript 是互联网上最流行的脚本语言,这门语言可用于 HTML 和 web ,更可广泛用于服务器,PC,笔记本电脑,平板电脑和智能手机等设备。JavaScript代码主要由浏览器去执行。
JavaScript 是一种轻量级的编程语言
JavaScript是能够插入到 html 标签语言中的代码
JavaScript是可插入 HTML 页面的编程代码
JavaScript 插入 HTML页面后,可由所有的现代浏览器执行

有了 JavaScript 编程语言,通过他就能够让你的网页活起来,能够让你一个静态的网页变成一个动态的网页,比如说你的一个网站,只能查看一些静态资源,有了 JavaScript 他能够让你的网站支持各种各样的功能,比如说,登录注册,弹窗,禁止复制粘贴等各种各样的功能。
趣谈静态网页
静态资源
在网页设计中,纯 HTML 格式的网页 文件(在 HTML 文件中,包含只有图片,视频,JS代码,CSS代码等样式) 通常被称作"静态网页"(静态网页没有和数据库打交道,仅仅是从服务器磁盘上,读取数据,返回给用户查看)
静态网页是相对于动态网页而言的,是指没有后台数据库,不包含程序,不可交互的网页。
静态网页的特点: 开发人员写了什么样,用户看到的就是固定的什么样,显示器就是什么样,一旦静态网页编写完成,就不会有在任何改变。静态网页一般主要适用于更新较少的展示型网页功能,例如(比如卖古董,它只展示一些常年不怎么动的古董图片)比如家具,酒水,水果宣传站点,适合中小型网站适合的搭建方式
静态网页资源对应文件扩展名为
-
纯文本文件,例如 .htm .html .xml(数据交互文件) .js .css
-
图片或数据文档,如 .jpg .bmp(高清) .txt .ppt .png .gif
-
视频类文件,如 .mp4 .avi .flv等
静态网页重要特性
-
每个页面有一个固定的 url 地址,url 地址不含有问号 "?"或"&"等符号
-
http://pythonay.cn/guoda.gif http://pythonay.cn/guoda.jpg
-
-
网页一经发布到服务器,网页内容是保存在服务器文件系统上的,每个网页都是独立的一个文件
-
网页内容固定不变,容易被搜索引擎收录(优点)
-
网页没有数据库支撑,在网站制作和维护上工作量很大(缺点)
-
网页的交互性很差,缺少程序的动态功能实现加载(缺点)
-
客户端解析网址时,由于不需要读取数据库,因此服务器端可以接受更高的并发访问,请求到来时,直接从磁盘上返回数据。(优点)
举例 (吃火锅,现成的蔬菜)
【有关高并发架构思想】
在高并发,高访问量的场景下做架构优化时,比较关键的就是把动态网页转化成静态网页,而不是直接请求数据库和动态服务器,并。。。
博客园官网
https://www.cnblogs.com/
趣谈动态网页
动态网页资源
1. 服务端需要通过执行程序做出处理,发送给客户端的是程序的运行结果
2. 动态网页是和静态网页相对而言的,动态网页的 url后缀一般是 .asp .aspx .php .js .cgi
3. 并且动态网页都有标志性的符号 "? &",后端都有数据库的支持。
动态网页
包含了静态网页的内容,以及能够和数据库交互,有后台程序,可以和用户交互的网页。
目前大部分网站都是静态网页的内容结合动态网页的功能搭建的网站。
动态网页地址
添加新随笔 https://i.cnblogs.com/EditPosts.aspx?opt=1
动态网页资源的特点
1. 网页以数据库技术为支撑,大大降低网站维护的工作量
2. 动态网页技术的网站可以实现更多的功能,如用户注册,用户登录,投票,用户管理,博客管理,点赞,网站后台程序等
3. 动态网页不是独立存在服务器上的网页文件,用户请求动态程序时,服务器解析程序并且可能读取数据库返回一个完整的网页内容
4. 搜索引擎(爬虫)一般不会抓取网址中的 "?"后面的内容,因此企业都会做伪静态技术页面(让一个动态网页,模拟成以 .html 为后缀的静态网页)
举例(饭店炒菜,现做)
趣谈并发模型
网站并发压力
并发: 保证一个网站7X24正常运行,还得保证效率
比如我们去淘宝购物,我们能够打开网页,但是我付款购买,它购买响应的时间特别慢,这样肯定不行的
又或者说,现在去小米商城出了一个秒杀活动,让我去秒杀手机,我准时准点想要去抢购手机,到点网站崩溃了,这对我来说是不是非常糟心的体验,在我们生活中,也有各种各样的事情,拥挤,堵塞,这些词,这些都是非常常见的,我们去超市排队,去银行排队,下班回家堵车,都很让人着急,我们都希望能快速的解决这些问题,处理效率高一点点。这和我们日常的上网也是一样,我们浏览网页,网页迅速的给与反馈,响应我们早已觉得理所当然,然而也会在一些特殊时候,例如淘宝的双11活动,某电商的秒杀活动等,超时间内,网站浏览人数骤增,网站的压力迅速增长,能够处理请求的能力也随之变弱,这就好比一个商场搞促销活动,一下子涌进了很多人,超市整个的购买能力就会下降许多了。 
并发模型
进程是linux的资源单位 包工头 分配工作的
线程是由进程发起的工作单位 工人 干活的
单进程模式
单进程和单线程是一个概念,因为一个进程单位必须要一个线程单位在工作
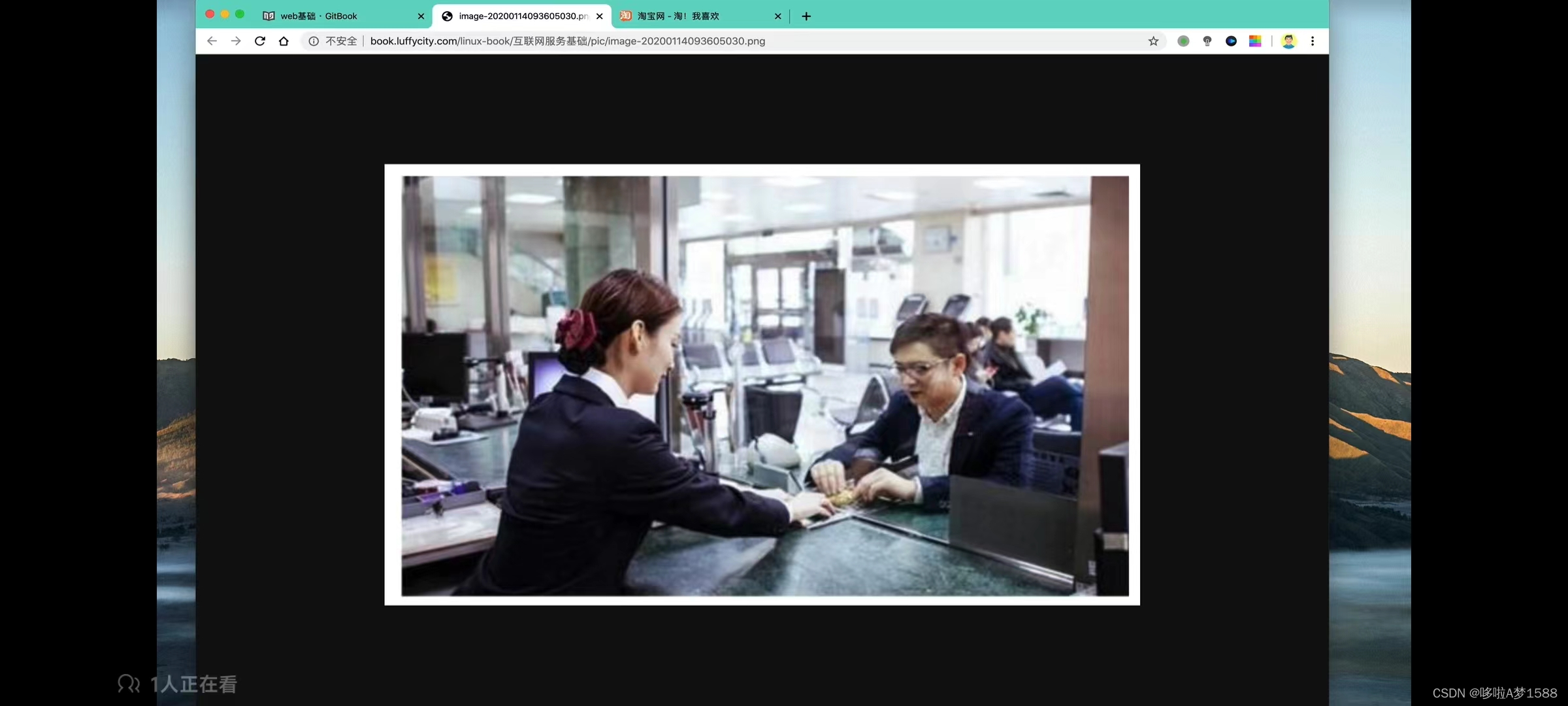
当大量请求进入服务器的时候,单线程(银行只有一个处理业务的窗口)情况下,一个一个去处理请求,请求很容易积压,得不到响应,这是一种没有并发概念的模式。
假设你去银行办业务,银行只开了一个窗口,即一个柜台,假设处理一个客户需要5分钟,大厅来了10个人在等待,要办业务,有一个人在办理业务,其他9人就只能干等着,如果说后面排队的人太多,保安会拒绝后来的人进入银行,让他们在外面等着,这就是生活中一个形象的比喻。也就是说,一台服务器,他是单进程处理请求的,一次只能处理一个请求,剩余的请求排队,当服务器器的连接数满了,服务器就会拒绝后面的流量,
【多进程模式】
银行规模扩大,柜台数也扩张,此时扩展为10个柜台,同时可以处理业务,当要100个用户,还要90个等待,同样的如果大厅排队人数过多,保安也禁止客户进入了。有同学问,那你为啥不开一百个窗口,这不要成本吗?一百个窗口得多大场地,招来100个客服,即使一上午只有5-6人,。。。银行的柜台,窗口 可以理解为进程单位
柜台后干活的工作人员 可以理解为线程单位这就是服务器的多进程工作模式,服务器有多个进程处理客户端的请求
主进程(master) 监听服务器80端口以及用户连接数,当客户请求来临,主进程fork(派生)出一个子进程来处理连接,子进程。。。父进程(主进程)继续等待其他客户的请求连接,但是进程占用服务器资源较多,服务器负载会升高。父进程启动多个子进程,每个子进程响应一个请求主进程(请求分配)子进程1(干活的进程)子进程2(干活的进程)子进程3(干活的进程)子进程4(干活的进程)子进程5(干活的进程)
这样的设计好处是隔离性,即使挂掉某一个子进程也不影响父进程,缺点是对系统资源消耗较大。
【复用的IO结构】
银行开10个窗口假设已是极限,如何还能加快事情的处理效率?
-
原本一个柜台只有一个客服,处理一个客户要5分钟
-
现在每个柜台安排多个工作人员,第一个人负责客户问题接待,第二个人负责票据打印,第三个人负责备案文档...
-
如此这般,当第二工作人员打印票票据的时候,第一个工作人员,又可以接待下一个客户、
-
对于用户而言,无感知后台的工作人员是几位,处理一个客户问题的时间大大缩短了
这种模式是一个进程响应n个请求,但并不是单纯的一个进程,而是背后的多线程在工作。
HTTP协议请求与响应流程如下图所示

服务器接收请求与响应请求的流程(HTTP请求与响应)
HTTP请求与响应流程大白话解释:
我们可以从上图看出,他分了7个步骤,整个过程如下:
第一步,客户端建立连接
也就是指你在浏览器访问了一个网站,输入了一个域名,比如想访问 baidu.com jd.com 等等,当你浏览器请求发出去之后,他是通过网络,通过HTTP协议,然后解析到TCP/IP层,因为域名要解析成IP地址,找到互联网中这太服务器淘宝,或者百度,京东他们这台服务器,我们向他们服务器寻求资料,通过tcp/ip协议,这个时候服务器接收到了请求,服务器只是 linux 的操作系统,他会把请求发送给手下干活的工人,他就是HTTP服务器,这个HTTP服务器是处于用户空间的,和用户离得最近的一款软件,(我们会在后面学习apache,nginx,web服务器)这时候,linux内核把用户的请求发给了HTTP服务器,它在这里对用户的请求进行解析,这个用户是想要图片,还是资料?视频?又或者是一个 html静态文件,又比如用户不仅是静态资源,它可能想要的是动态的请求,需要后端程序以及数据库进行一个交互,然后最终把数据库中的数据返回给用户,将动态的请求处理一下,这个时候web服务器,会在(3)这里判断到底是静态还是动态?假如是一个静态请,这个时候http服务器就会去内核空间,会通过linux系统,去访问磁盘上的资料,又或者是网络文件系统,这里指的是存储,它可以是存储,也可以是文件,或者是网络共享文件系统等,这时候静态资源到(4),访问存储资源,读取到后就是第(5)构建响应,资源返回给HTTP(web服务器)拿到了数据,它会构建一个响应头,响应体,告诉用户,你请求的数据是走什么协议的,什么类型的,大小以及客户端地址等等一些信息,构建响应然后走到了(6)发送响应,把数据给用户返回,用户在电脑上就看到了你服务器上的图片,文本,等信息,最终 web 服务器它会把一整套流程记录下来(7)记录事务处理整个流程。做一个日志记录,用于运维人员做运维操作。这是服务器接收请求与响应请求的一个流程HTTP请求与响应流程
1. 客户端和服务器建立连接,客户端发出请求,和服务器进行三次握手身份确认。
2. 服务器接收到请求,linux 内核根据(客户端的请求) socket 进程通信管道把请求发给了HTTP应用程序去解析(apache,nginx 主流的web服务器)
3. HTTP服务器开始处理请求,对用户的请求报文进行解析明确客户端需要的资源和请求方式等等。(get,post)
4. HTTP在存储系统上,请求资源,内核去本地文件系统上,读取数据
5. HTTP服务器构造响应体,应用程序创建响应报文
6. linux 内核发出HTTP服务器构造的响应报文,发送客户端
7. HTTP服务器会进行事务记录,记录整个流程的日志
HTTP的发展史

趣谈事务概念
事务
在计算机领域中
事务是指程序中一系列严密的逻辑性操作,并且必须保证所有操作都能够成功的完成,如果出错,那么得保证每个操作中的更改动作,都会被撤销
简单理解
多件事情当做一件事情来处理,好比大家都在同一条船,要么一起前进,存活,要么一起被撤销
在数据库领域,来理解事务
比如转账的事务
A用户从自己的账户转出1000元给B的账户,那么当这个A用户从转账开始到B用户收款成功后,这一系列的过程称之为是一个事务。
事务的一些特性:
-
原子性 我们在计算机执行命令,要么全部成功,要么全部失败。只要有一个环节出错,那么其他指令都要进行数据回滚。回滚到执行命令之前的操作。
-
一致性:事务的执行使得数据从一个状态,进入到另一个状态,但是对于的数据完整性,还是保存稳定。
-
隔离性:比如当多个用户并发访问数据库的时候,共同操作一张数据表,数据库它会为每一个用户开启事务,不能被其他的事务干扰,多个并发的事务操作,要进行隔离。
-
持久性:当事务正确完成后,对数据的修改是永久性的。
HTTP事务原理
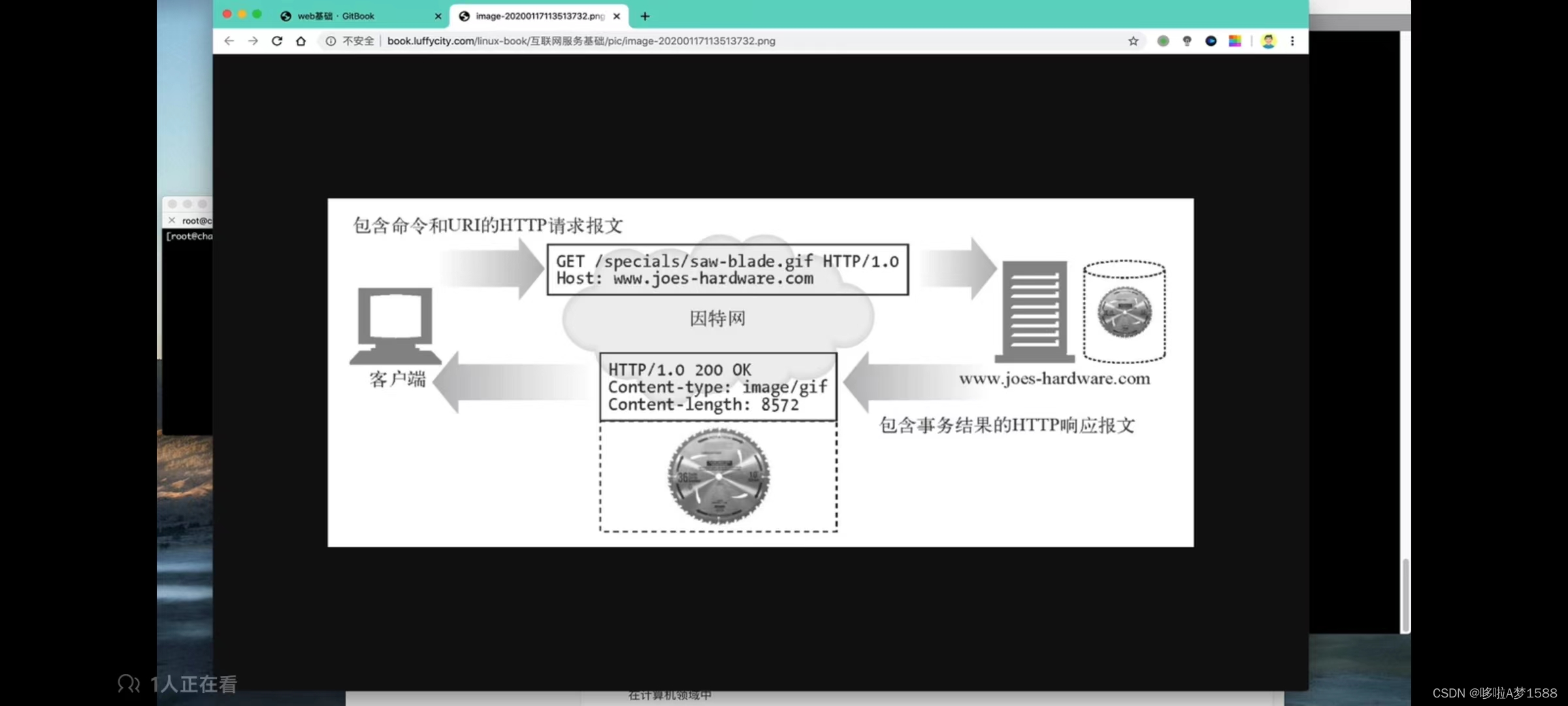
# 包含命令和URL的HTTP请求报文从上图我们可以看出,这是一个HHTP请求与响应的过程,客户端发送一个请求,带着一个URL和请求报文,如下:'GET /specials/saw-blade.gif HTTP/1.0 Host: www.joes-hardware.com'请求参数解释
'GET' 代表一个请求动作
'Host': 服务器主机
'/specials/saw-blade.gif': 请求要的资料
'HTTP/1.0': 该请求走的协议
'www.joes-hardware.com' : 该服务器主机的域名# 包含事务结果的HTTP响应报文 如下:
HTTP/1.0 200 OK
Content-type: image/gif
Content-length: 8572响应返回参数解释
'HTTP/1.0' : 响应返回使用的通信协议
'200' : 表示已经成功返回客户端请求的资料 状态码,不同的状态码能够表示HTTP的处理结果
'Content-type' : 表示传输的类型
'image/gif': 表示是返回的是图片
'Content-length': 表示发送的数据大小长度HTTP事务流程
在浏览器中输入网站直到最终看到页面的整个过程,叫做HTTP事务过程
在浏览器中输入:book.luffcity.com
系统会做什么事情?
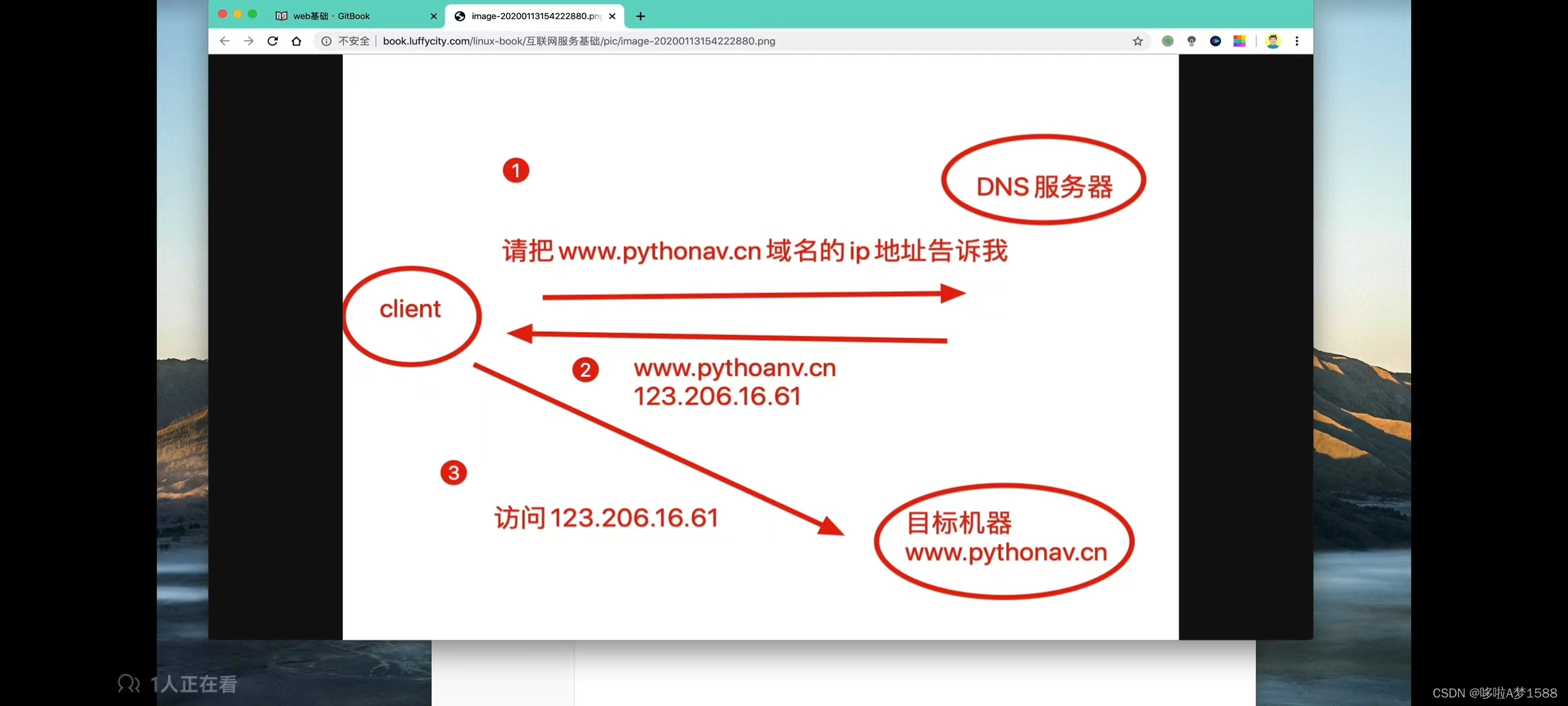
1. DNS解析流程
1. dns 解析
在浏览器中输入:book.luffcity.com 浏览器会解析域名对应的IP地址,
2. 浏览器去客户端本地机器寻找 NDS 缓存,是否存在解析记录
3. 若没有找到,浏览器会继续读取客户端本地的hosts文件,是否写死了,该域名对应的IP地址
4.如果以上查找都没有,浏览器会再向本地配置的NDS服务器地址,进行解析请求发送,公网的DNS服务器对该域名解析,解析到IP地址之后,浏览器会访问该IP地址。
2. 客户端此时和服务端建立 TCP/IP 三次握手
1. 客户端解析到服务端的IP之后,客户端的user-agent(身份)是正常的浏览器,谷歌浏览器,等等浏览器,浏览器会以本地的(<1024端口>端口<65535端口>)向服务器的80端口进行请求发送,进行三次握手
2. 该客户端请求,经过成 TCP/IP 的四层封包之后。请求最终进入到服务器的应用程序。完成解包的过程。最终和客户端建立 TCP 连接
3. 此时 TCP 连接上之后,开始三次握手。第一次握手: 客户端发送 syn 包(syn=x) 发送给服务器,客户端进入 syn_send 状态,等待服务器响应
第二次握手: 服务器收到客户端的 syn 包,并且要确认客户端的SYN(ack=x+1),同时服务器再发出一个SYN包(syn=k),服务器一共发送的是 syn+ack数据包,服务器进入 syn_recv 状态。
第三次握手: 客户端收到服务器发来的 syn+ack 包,客户端再向服务器发送 ACK(k+1),此时服务端和客户端已经正确建立了连接。完成三次握手。客户端和服务器进入长连接的状态三次握手结束以后,客户端才开始正式发送数据给服务器客户端和服务器的端口,也需要进行一个四次挥手的过程,也就是服务器再次和客户端进行信号数据包发送,确认对方都要 TCP 断开。3. 数据传输,发起HTTP请求
1.如何查看用户发出的请求动作,请求方法是什么呢?
a. 使用 web 服务器的日志功能查看
b. 使用浏览器的开发者模式查看nginx 官网:
https://nginx.org/
https://nginx.org/en/download.htmlsudo apt update
sudo apt install nginxroot@ubuntu-master:/opt# nginx -V
nginx version: nginx/1.18.0 (Ubuntu)
built with OpenSSL 3.0.2 15 Mar 2022
TLS SNI support enabled
configure arguments: --with-cc-opt='-g -O2 -ffile-prefix-map=/build/nginx-zctdR4/nginx-1.18.0=. -flto=auto -ffat-lto-objects -flto=auto -ffat-lto-objects -fstack-protector-strong -Wformat -Werror=format-security -fPIC -Wdate-time -D_FORTIFY_SOURCE=2' --with-ld-opt='-Wl,-Bsymbolic-functions -flto=auto -ffat-lto-objects -flto=auto -Wl,-z,relro -Wl,-z,now -fPIC' --prefix=/usr/share/nginx --conf-path=/etc/nginx/nginx.conf --http-log-path=/var/log/nginx/access.log --error-log-path=/var/log/nginx/error.log --lock-path=/var/lock/nginx.lock --pid-path=/run/nginx.pid --modules-path=/usr/lib/nginx/modules --http-client-body-temp-path=/var/lib/nginx/body --http-fastcgi-temp-path=/var/lib/nginx/fastcgi --http-proxy-temp-path=/var/lib/nginx/proxy --http-scgi-temp-path=/var/lib/nginx/scgi --http-uwsgi-temp-path=/var/lib/nginx/uwsgi --with-compat --with-debug --with-pcre-jit --with-http_ssl_module --with-http_stub_status_module --with-http_realip_module --with-http_auth_request_module --with-http_v2_module --with-http_dav_module --with-http_slice_module --with-threads --add-dynamic-module=/build/nginx-zctdR4/nginx-1.18.0/debian/modules/http-geoip2 --with-http_addition_module --with-http_gunzip_module --with-http_gzip_static_module --with-http_sub_module
root@ubuntu-master:/opt## 使用 web 服务器的日志功能查看,看出用户发出的请求是 'GET' 请求,获取服务器资料
root@ubuntu-master:~# tail -l /opt/ngx112/logs/access.log
3.22.71.133 - - [06/Apr/2020:14:36:09 +0800] "GET /favicon.ico HTTP/1.1" 404 200 "http://pythonav.cn/" "Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML,like Gecko) Chrome/75.0.3770.142 Sarari/537.36" "-"参数解释
'[06/Apr/2020:14:36:09 +0800]': 什么时间请求的
'GET /favicon.ico HTTP/1.1' : 请求的内容是什么
'GET': 拿,获取的意思
'/favicon.ico': 获取服务器的一个图标文件
'HTTP/1.1': http协议版本1.1
'404 200': 返回的状态码# 使用浏览器的开发者模式查看
F12----network--点击请求的资源名,查看请求头
例如某一个HTTP请求日志记录
3.22.71.133 - - [06/Apr/2020:14:36:09 +0800] "GET /favicon.ico HTTP/1.1" 404 200 "http://pythonav.cn/" "Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML,like Gecko) Chrome/75.0.3770.142 Sarari/537.36" "-"
[request Method] (常见的 HTTP 请求方法)
GET, 向服务器获取数据,资源
POST, 向服务器提交数据,登录,注册
HEAD, 获取URL的响应头信息(只要脑袋),不要响应主体信息(不要身体数据)
PUT, 将请求主体部分发给服务器
DELETE, 删除服务器指定的资源
TRACE, 追踪请求到达服务器发生的变动
OPTIONS, 让服务器返回对指定的URL支持的所有请求方法[URL请求体]
GeneralRequest URL: http://pythonav.cn/Request Method: GETStatus Code: 304 Not ModifiedRemote Address: 123.206.16.61:80Referrer Policy: no-referrer-when-downgradeResponse Headers view sourceAccept-Ranges: bytesContent-Length: 9503Content-Type: text/htmlDate: Fri,17 Jan 2020 06:29:13 GMTServer: nginx/1.12.0Request Headers view sourceAccept: text/html,application/xhtml+xml,application/xml;q=0.9,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.9Accept-Encoding: gzip,deflateAccept-Language: zh-CN,zh:q=0.9Cache-Control: max-age=0Connection: keep-aliveCookie: Hm_lvt_7158c55a533ed0cf57dede022b1e6aed=1573435487;_ga=GA1.2.1264774190.1573435488Host: pythonav.cnIf-Modified-Since: Mon,06 Jan 2020 06:29:13 GMTIf-None-Match: "Se12d3b9-251f"Upgrade-Insecure-Request: 1User-Agent: Mozilla/5.0 (Macintosh: Intel Mac os x 10_15_2) Applewebkit/537.36 (KHTML.Like Gecko ) Chrome/79.0.3945.117 Safari/537.36-
Accept 就是告诉服务器端,我接受那些MIME类型
-
Accept-Encoding 这个看起来是接受那些压缩方式的文件
-
Accept-Lanage 告诉服务器能够发送哪些语言
-
Connection 告诉服务器支持 keep-alive 特性
-
Cookie 每次请求时都会携带上Cookie以方便服务器识别是否是同一个客户端
-
Host 用来标识请求服务器上的那个虚拟主机,比如Nginx里面可以定义很多
-
虚拟主机,那这里就是用来标识要访问那个虚拟主机。
-
User-Agent 用户代理,一般情况是浏览器,也有其他类型,如:wget curl 搜索引擎的蜘蛛灯
-
If-Modified-Since 是浏览器向服务器端询问某个资源文件如果自从什么时间修过,那么重新发给我,这样就保证服务器端资源,文件更新时,浏览器再次去求,而不是使用缓存中的文件。
-
If-None-Match: 本地缓存中存储的文档的ETag标签是否与服务器文档的Etag不匹配;
-
常见的 HTTP 请求方法
get 向服务器获取资源,等等
post 向服务器提交数据,比如 登录,注册,
head 获取 URL 的响应头信息,不要响应体信息(只要脑袋,不要身体)
put 将请求主体发送给服务器
delete 删除服务器指定的一些资源
trace 追踪请求到达服务器的一些列变动(开发人员在监测请求流程时用的)
[状态码]
HTTP状态码是用以表示网页服务器超文本传输协议响应状态的3位数字代码
HTTP请求状态如何,用状态码表示结果
状态码类别
1xx 信息状态码,服务器收到请求,需要客户端继续操作
2xx 操作成功
3xx 重定向状态码,需要进一步的操作
4xx 客户端错误,请求语法错误等
5xx 服务端错误,服务器处理过程中出错了常见状态码
一些常见的HTTP状态码为:
200--服务器成功返回网页
404--请求网页不存在
503--服务不可用常见 HTTP 状态码大全
1xx (临时响应)
表示临时响应并需要请求者继续执行操作的状态代码。代码 说明
http 状态码 100 (继续) 请求者应当继续提出请求。服务器返回此代码表示已收到请求的第一部分,正在等待其余部分
http 状态码 101 (切换协议) 请求者已要求服务器切换协议,服务器已确认并准备切换。2xx (成功)
表示成功处理了请求的状态码。
代码 说明
http 状态码 200 (成功) 服务器成功处理了请求,通常,这表示服务器提供了请求的网页。
http 状态码 201 (已创建) 请求成功并且服务器创建了新的资源。
http 状态码 202 (已接受) 服务器已接受请求,但尚未处理。
http 状态码 203 (非授权信息) 服务器已成功处理了请求,但返回的信息可能来自另一来源。
http 状态码 204 (无内容) 服务器成功处理了请求,但没有返回任何内容。
http 状态码 205 (重置内容)服务器成功处理了请求,但没有返回任何内容。
http 状态码 206 (部分内容)服务器成功处理了部分 GET 请求。3xx (重定向)
表示要完成请求,需要进一步操作。通常,这些状态代码用来重定向。代码 说明
http 状态码 300 (多种选择) 针对请求,服务器可执行多种操作。服务器可根据请求者(user agent) 选择一项操作
http 状态码 301 (永久移动) 请求的网页已永久移动到新位置。服务器返回此响应 (对GET 或 HEAD请求的响应)时
http 状态码 302 (临时移动) 服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求
http 状态码 303 (查看其他位置) 请求者应当对不同的位置使用单独的 GET 请求来检索响应时,服务器返回此代码。
http 状态码 304 (未修改) 自从上次请求后,请求的网页未修改过。服务器返回此响应时,不会返回网页内容。
http 状态码 305 (使用代理) 请求者只能使用代理访问请求的网页。如果服务器返回此响应,还表示请求者应使用代理
http 状态码 307 (临时重定向) 服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求。4xx (请求错误)
这些状态代码表示请求可能出错,妨碍了服务器的处理。代码 说明
http 状态码 400 (错误请求) 服务器不理解请求的语法。
http 状态码 401 (未授权) 请求要求身份验证。对于需要登录的网页,服务器可能返回此响应。
http 状态码 403 (禁止) 服务器拒绝请求
http 状态码 404 (未找到) 服务器找不到请求的网页。
http 状态码 405 (方法禁用) 禁用请求中指定的方法
http 状态码 406 (不接受) 无法使用请求的内容特性响应请求的网页
http 状态码 407 (需要代理授权) 此状态码与401(未授权)类似,但指定请求者应当授权使用代理。
http 状态码 408 (请求超时) 服务器等候请求时发生超时。
http 状态码 409 (冲突) 服务器在完成请求时发生冲突。服务器必须在响应中包含有关冲突的信息。
http 状态码 410 (已删除) 如果请求的资源已永久删除,服务器就会返回此响应。
http 状态码 411 (需要有效长度) 服务器不接受不含有效内容长度标头字段的请求。
http 状态码 412 (未满足前提条件) 服务器未满足请求者在请求中设置的其中一个前提条件。
http 状态码 413 (请求实体过大) 服务器无法处理请求,因为请求实体过大,超出服务器的处理能力。
http 状态码 414 (请求的URL 过长) 请求的 URL (通常为网址)过长,服务器无法处理。
http 状态码 415 (不支持的媒体类型) 请求的格式不受请求页面的支持。
http 状态码 416 (请求范围不符合要求) 如果页面无法提供请求的范围,则服务器会返回此状态代码。
http 状态码 417 (未满足期望值) 服务器未满足 "期望" 请求标头字段的要求。5xx (服务器错误)
这些状态代码表示服务器在尝试处理请求时发生内部错误。这些错误可能是服务器本身的错误,而不是请求出错。代码 说明
http 状态码 500 (服务器内部错误) 服务器遇到错误,无法完成请求。
http 状态码 501 (尚未实施) 服务器不具备完成请求的功能。例如,服务器无法识别请求方法时可能会返回此代码。
http 状态码 502 (错误网关) 服务器作为网关或代理,从上游服务器收到无效响应。
http 状态码 503 (服务不可用) 服务器目前无法使用 (由于超载或停机维护)。通常,这只是暂时状态。
http 状态码 504 (网关超时) 服务器作为网关或者代理,但是没有及时从上游服务器收到请求。
http 状态码 505 (HTTP 版本不受支持) 服务器不支持请求中所用的 HTTP 协议版本。[响应头信息]
Response Headers view sourceAccept-Ranges: bytesContent-Length: 9503Content-Type: text/htmlDate: Fri,17 Jan 2020 06:27:18 GMTEtag: "5e12d3b9-251f"Last-Modified: Mon,06 Jan 2020 06:29:13 GMTServer: nginx/1.12.0Connection # 使用 keep-alive 特性Content-Encoding # 使用 gzip 方式对资源压缩Content-Length: 主体的长度Content-type: # MIME类型为html类似,字符集是 UTF-8Date # 响应的日期Server # 使用 WEB 服务器Last-Modified # 最后一次修改时间Server: # 服务器程序软件名称和版本
4.浏览器解析 HTML
浏览器拿到 index.html 文件之后,解析 html 网页文件,遇见静态资源(js,css,img) 就去服务器再次发请求下载,这个时候就用上 keep-alive 特性了,建立一次HTTP 连接,可以请求多个资源,下载资源的顺序就是按照代码里的顺序,但是由于每个资源大小不一样,而浏览器又多线程请求资源,顺序并不一定是代码里面的顺序。
view-source:哔哩哔哩 (゜-゜)つロ 干杯~-bilibili/index.html
https://www.bilibili.com/index.html<!DOCTYPE html>
<html lang="zh-CN" class="gray"><head><meta charset="UTF-8" /><title>哔哩哔哩 (゜-゜)つロ 干杯~-bilibili</title><metaname="description"content="哔哩哔哩(bilibili.com)是国内知名的视频弹幕网站,这里有及时的动漫新番,活跃的ACG氛围,有创意的Up主。大家可以在这里找到许多欢乐。"/><metaname="keywords"content="bilibili,哔哩哔哩,哔哩哔哩动画,哔哩哔哩弹幕网,弹幕视频,B站,弹幕,字幕,AMV,MAD,MTV,ANIME,动漫,动漫音乐,游戏,游戏解说,二次元,游戏视频,ACG,galgame,动画,番组,新番,初音,洛天依,vocaloid,日本动漫,国产动漫,手机游戏,网络游戏,电子竞技,ACG燃曲,ACG神曲,追新番,新番动漫,新番吐槽,巡音,镜音双子,千本樱,初音MIKU,舞蹈MMD,MIKUMIKUDANCE,洛天依原创曲,洛天依翻唱曲,洛天依投食歌,洛天依MMD,vocaloid家族,OST,BGM,动漫歌曲,日本动漫音乐,宫崎骏动漫音乐,动漫音乐推荐,燃系mad,治愈系mad,MAD MOVIE,MAD高燃"/><meta name="renderer" content="webkit" /><meta http-equiv="X-UA-Compatible" content="IE=edge" /><meta name="spm_prefix" content="333.1007" /><meta name="referrer" content="no-referrer-when-downgrade" /><meta name="applicable-device" content="pc"><meta http-equiv="Cache-Control" content="no-transform" /><meta http-equiv="Cache-Control" content="no-siteapp" /><meta name="server_render" content="is_server_render" /><link rel="dns-prefetch" href="//s1.hdslb.com" /><link rel="apple-touch-icon" href="https://i0.hdslb.com/bfs/static/jinkela/long/images/512.png" /><link rel="shortcut icon" href="https://www.bilibili.com/favicon.ico?v=1" /><link rel="canonical" href="https://www.bilibili.com/" /><link rel="alternate" media="only screen and (max-width: 640px)" href="https://m.bilibili.com" /><linkrel="stylesheet"href="//s1.hdslb.com/bfs/static/jinkela/long/font/medium.css"media="print"onload="this.media='all'"/><linkrel="stylesheet"href="//s1.hdslb.com/bfs/static/jinkela/long/font/regular.css"media="print"onload="this.media='all'"/><script>window._BiliGreyResult={"method":"gray","grayVersion":"22117"}</script><script src="//s1.hdslb.com/bfs/static/laputa-home/client/assets/svgfont.9cb2f5e1.js" async></script><script src="https://www.bilibili.com/gentleman/polyfill.js?features=es2015%2Ces2016%2Ces2017%2Ces2018%2Ces2019%2Ces2020%2Ces2021%2Ces2022%2CglobalThis&flags=gated"></script> <script type="text/javascript" src="//s1.hdslb.com/bfs/seed/jinkela/short/bmg/register/fallback.js"></script><link rel="stylesheet" href="//s1.hdslb.com/bfs/static/jinkela/long/laputa-css/map.css"/><link rel="stylesheet" href="//s1.hdslb.com/bfs/static/jinkela/long/laputa-css/light_u.css"/><link id="__css-map__" rel="stylesheet" href="//s1.hdslb.com/bfs/static/jinkela/long/laputa-css/light.css"/><script>window.__SERVER_CONFIG__={"serverBuvid":"FFE11A3D-7201-5684-5E4B-A0E07C0EE75D49463infoc","homeFeedColumn":"5","browserResolution":"1536-252","isModern":true,"aiexp":"3","remove_channel_lift":0,"ab_test":{"for_ai_home_version":"V8","tianma_banner_inline":"CONTROL","in_theme_version":"CLOSE","exit_feed_btn":"HIDE","force_to_feed":"GO","enable_web_push":"DISABLE"},"constants":{"previewTipCountingSecond":1,"previewCountingSecond":4,"nanoVersionHash":"a8c001e3","nanoVersionPipHash":"71a769ad","nanoVersionPcdnHash":"57abf745","tianma_banner_inline_V0":-1,"tianma_banner_inline_V1":10},"uniq_page_id":140999651034};</script><script type="text/javascript">window.__NANO_VERSION_HASH__ = "a8c001e3"</script><script type="text/javascript">// 当没有值时,给一个合适页面使用的if (!window.__NANO_VERSION_HASH__) {window.__NANO_VERSION_HASH__ = 'a8c001e3'}</script><script type="text/javascript">;(function () {if (document.querySelector('meta[name=server_render]')) {return}var ua = window.navigator.userAgent,agents = ['Android', 'Phone', 'SymbianOS', 'iPod'],isPC = trueif (/\sVR\s/g.test(ua)) returnfor (var i = 0, len = agents.length; i < len; i++) {if (ua.indexOf(agents[i]) > 0) {isPC = falsebreak}}if (!isPC) {window.location.href = window.location.href.replace('www', 'm')}})()</script><script type="text/javascript">window.spmReportData = {}window.reportConfig = {sample: 1,msgObjects: 'spmReportData',errorTracker: true}function getCookie(name) {var reg = new RegExp('(^| )' + name + '=([^;]*)(;|$)')var r = document.cookie.match(reg)return r ? unescape(r[2]) : null}function fsrCb() {if (window.performance && window.performance.timing) {window.performance.timing.firstscreenfinish = new Date().getTime()}}// 图片降级使用function imgOnError(img) {typeof window.imgAutoFallbackOnError === 'function' && window.imgAutoFallbackOnError(img)}// 图片降级使用function imgOnLoad(img) {typeof window.imgAutoFallbackOnLoad === 'function' && window.imgAutoFallbackOnLoad(img)}function lqipCb(img) {var lqip =img && img.parentNode && img.parentNode.querySelector('.lqip')if (lqip) {lqip.classList.add('is-active')}}if (history.scrollRestoration) {history.scrollRestoration = 'manual'}window.page_load_time = Date.now()</script><script type="text/javascript">if (!window.abtest) {window.abtest = {'b_ut': getCookie('b_ut'),'home_version': 'V8','i-wanna-go-back': getCookie('i-wanna-go-back'),'in_new_ab': true,'ab_version': {"for_ai_home_version":"V8","tianma_banner_inline":"CONTROL","in_theme_version":"CLOSE","exit_feed_btn":"HIDE","force_to_feed":"GO","enable_web_push":"DISABLE"},'ab_split_num': {"for_ai_home_version":0,"tianma_banner_inline":0,"in_theme_version":30,"exit_feed_btn":67,"force_to_feed":32,"enable_web_push":19},}}</script><scripttype="text/javascript"src="//s1.hdslb.com/bfs/seed/log/report/log-reporter.js"></script><script src="//s1.hdslb.com/bfs/seed/media-preview/core.4fe40c36.js"></script><!--preload-fetch--><script type="module" crossorigin src="//s1.hdslb.com/bfs/static/laputa-home/client/assets/index.2fbb75b2.js"></script><link rel="modulepreload" href="//s1.hdslb.com/bfs/static/laputa-home/client/assets/vendor.6e0e8550.js"><link rel="stylesheet" href="//s1.hdslb.com/bfs/static/laputa-home/client/assets/vendor.54c577aa.css"><link rel="stylesheet" href="//s1.hdslb.com/bfs/static/laputa-home/client/assets/index.84c9e904.css"><script type="module">try{import("_").catch(()=>1);}catch(e){}window.__vite_is_dynamic_import_support=true;</script><script type="module">!function(){if(window.__vite_is_dynamic_import_support)return;console.warn("vite: loading legacy build because dynamic import is unsupported, syntax error above should be ignored");var e=document.getElementById("vite-legacy-polyfill"),n=document.createElement("script");n.src=e.src,n.onload=function(){System.import(document.getElementById('vite-legacy-entry').getAttribute('data-src'))},document.body.appendChild(n)}();</script></head><body><script>// bili-mirror 告警上报class MirrorBanReportBySelfDef {mirrorHandleBefore(type, data) {if (type === 'resource') {// 根据用户登录态来过滤const mid = document?.cookie?.split?.(';')?.find?.(item => item.includes('DedeUserID'))?.split?.('=')?.[1] ?? ''return Promise.resolve(!!mid)} else {return Promise.resolve(true)}}mirrorHandleAfter() {return Promise.resolve()}}window.__MIRROR_CONFIG__ = {origin: 'main',module: 'home-page',spmId: '333.1007',plugins: new MirrorBanReportBySelfDef(),config: {isAutoInit: true, // 注意这个属性,isAutoInit 为 true ,js 加载完成后会自动执行 init 方法whiteScreen: {maxLoop: 10,checkDom: ['#i_cecream'],callback: status => {console.log('白屏检测是否正常', status)},isSkeleton: false}}}</script><script src="//s1.hdslb.com/bfs/seed/jinkela/short/b-mirror/biliMirror.umd.mini.js"></script><div class="browser-tip"></div><script>if (window.__SERVER_CONFIG__ &&window.__SERVER_CONFIG__.isModern === false) {document.querySelector('.browser-tip').innerHTML ='<div class="title">当前浏览器版本较低,为保证您的使用体验,建议使用最新版本的浏览器访问。</div>'}if (/(Mac|iPhone|iPod|iPad)/i.test(window.navigator.platform)) {document.body.classList.add('mac')} else {document.body.classList.add('win')}</script><div id="i_cecream"><!--[--><!--[--><div class="bili-video-card__wrap __scale-wrap __adblockhidden" data-v-7f4a51a0><a href="//cm.bilibili.com" data-target-url="**" data-v-7f4a51a0></a></div><!----><!--]--><div class="bili-feed4"><!--[--><div class="bili-header large-header"><div class="bili-header__bar"><ul class="left-entry"><li><a href="//www.bilibili.com" class="entry-title"><svg width="18" height="18" viewbox="0 0 18 18" fill="none" xmlns="http://www.w3.org/2000/svg" class="zhuzhan-icon"><path fill-rule="evenodd" clip-rule="evenodd" d="M3.73252 2.67094C3.33229 2.28484 3.33229 1.64373 3.73252 1.25764C4.11291 0.890684 4.71552 0.890684 5.09591 1.25764L7.21723 3.30403C7.27749 3.36218 7.32869 3.4261 7.37081 3.49407H10.5789C10.6211 3.4261 10.6723 3.36218 10.7325 3.30403L12.8538 1.25764C13.2342 0.890684 13.8368 0.890684 14.2172 1.25764C14.6175 1.64373 14.6175 2.28484 14.2172 2.67094L13.364 3.49407H14C16.2091 3.49407 18 5.28493 18 7.49407V12.9996C18 15.2087 16.2091 16.9996 14 16.9996H4C1.79086 16.9996 0 15.2087 0 12.9996V7.49406C0 5.28492 1.79086 3.49407 4 3.49407H4.58579L3.73252 2.67094ZM4 5.42343C2.89543 5.42343 2 6.31886 2 7.42343V13.0702C2 14.1748 2.89543 15.0702 4 15.0702H14C15.1046 15.0702 16 14.1748 16 13.0702V7.42343C16 6.31886 15.1046 5.42343 14 5.42343H4ZM5 9.31747C5 8.76519 5.44772 8.31747 6 8.31747C6.55228 8.31747 7 8.76519 7 9.31747V10.2115C7 10.7638 6.55228 11.2115 6 11.2115C5.44772 11.2115 5 10.7638 5 10.2115V9.31747ZM12 8.31747C11.4477 8.31747 11 8.76519 11 9.31747V10.2115C11 10.7638 11.4477 11.2115 12 11.2115C12.5523 11.2115 13 10.7638 13 10.2115V9.31747C13 8.76519 12.5523 8.31747 12 8.31747Z" fill="currentColor"></path></svg><span>首页</span></a></li><!----><!--[--><!--[--><li class="v-popover-wrap"><!--[--><a href="//www.bilibili.com/anime/" target="_blank" class="default-entry"><span>番剧</span></a><!--]--><!----></li><!----><!--]--><!--[--><li class="v-popover-wrap"><!--[--><a href="//live.bilibili.com" target="_blank" class="default-entry"><span>直播</span></a><!--]--><!----></li><!----><!--]--><!--[--><li class="v-popover-wrap"><!--[--><a href="//game.bilibili.com/platform" target="_blank" class="default-entry"><span>游戏中心</span></a><!--]--><!----></li><!----><!--]--><!--[--><li class="v-popover-wrap"><!--[--><a href="//show.bilibili.com/platform/home.html?msource=pc_web" target="_blank" class="default-entry"><span>会员购</span></a><!--]--><!----></li><!----><!--]--><!--[--><li class="v-popover-wrap"><!--[--><a href="//manga.bilibili.com?from=bill_top_mnav" target="_blank" class="default-entry"><span>漫画</span></a><!--]--><!----></li><!----><!--]--><!--[--><li class="v-popover-wrap"><!--[--><a href="//www.bilibili.com/match/home/" target="_blank" class="default-entry"><span>赛事</span></a><!--]--><!----></li><!----><!--]--><!--[--><!----><!----><!--]--><!--[--><!----><!----><!--]--><!--]--><li class="v-popover-wrap"><!--[--><a href="//app.bilibili.com" target="_blank" class="download-entry download-client-trigger"><svg width="16" height="16" viewbox="0 0 16 16" fill="none" xmlns="http://www.w3.org/2000/svg" class="download-client-trigger__icon"><path d="M7.23181 8.65895V1.75796C7.23181 1.33935 7.57582 1 8.00018 1C8.42453 1 8.76854 1.33935 8.76854 1.75796V8.67097L9.98589 7.47009C10.286 7.17409 10.7725 7.17409 11.0725 7.47009C11.3726 7.7661 11.3726 8.24601 11.0725 8.54201L8.54958 11.0308C8.24952 11.3268 7.76302 11.3268 7.46295 11.0308L4.94002 8.54201C4.63995 8.24601 4.63995 7.7661 4.94002 7.47009C5.24008 7.17409 5.72658 7.17409 6.02665 7.47009L7.23181 8.65895Z" fill="currentColor"></path><path d="M3.48023 4.29936C2.40686 4.29936 1.53672 5.15772 1.53672 6.21656V11.5669C1.53672 12.6257 2.40686 13.4841 3.48023 13.4841H12.5198C13.5931 13.4841 14.4633 12.6257 14.4633 11.5669V6.21656C14.4633 5.15772 13.5931 4.29936 12.5198 4.29936H11.6158C11.1915 4.29936 10.8475 3.96001 10.8475 3.5414C10.8475 3.12279 11.1915 2.78344 11.6158 2.78344H12.5198C14.4418 2.78344 16 4.3205 16 6.21656V11.5669C16 13.4629 14.4418 15 12.5198 15H3.48023C1.55815 15 0 13.4629 0 11.5669V6.21656C0 4.3205 1.55815 2.78344 3.48023 2.78344H4.38418C4.80853 2.78344 5.15254 3.12279 5.15254 3.5414C5.15254 3.96001 4.80853 4.29936 4.38418 4.29936H3.48023Z" fill="currentColor"></path></svg><span>下载客户端</span><!----></a><!--]--><!----></li></ul><div class="center-search-container"><div class="center-search__bar"><form id="nav-searchform" class="" style="border-radius:8px 8px 8px 8px;"><div class="nav-search-content"><input class="nav-search-input" type="text" autocomplete="off" accesskey="s" maxlength="100" x-webkit-speech="" x-webkit-grammar="builtin:translate" value="" placeholder="" title=""><div class="nav-search-clean"><svg width="16" height="16" viewbox="0 0 16 16" fill="none" xmlns="http://www.w3.org/2000/svg"><path fill-rule="evenodd" clip-rule="evenodd" d="M8 14.75C11.7279 14.75 14.75 11.7279 14.75 8C14.75 4.27208 11.7279 1.25 8 1.25C4.27208 1.25 1.25 4.27208 1.25 8C1.25 11.7279 4.27208 14.75 8 14.75ZM9.64999 5.64303C9.84525 5.44777 10.1618 5.44777 10.3571 5.64303C10.5524 5.83829 10.5524 6.15487 10.3571 6.35014L8.70718 8.00005L10.3571 9.64997C10.5524 9.84523 10.5524 10.1618 10.3571 10.3571C10.1618 10.5523 9.84525 10.5523 9.64999 10.3571L8.00007 8.70716L6.35016 10.3571C6.15489 10.5523 5.83831 10.5523 5.64305 10.3571C5.44779 10.1618 5.44779 9.84523 5.64305 9.64997L7.29296 8.00005L5.64305 6.35014C5.44779 6.15487 5.44779 5.83829 5.64305 5.64303C5.83831 5.44777 6.15489 5.44777 6.35016 5.64303L8.00007 7.29294L9.64999 5.64303Z" fill="#C9CCD0"></path></svg></div></div><div class="nav-search-btn"><svg width="17" height="17" viewbox="0 0 17 17" fill="none" xmlns="http://www.w3.org/2000/svg"><path fill-rule="evenodd" clip-rule="evenodd" d="M16.3451 15.2003C16.6377 15.4915 16.4752 15.772 16.1934 16.0632C16.15 16.1279 16.0958 16.1818 16.0525 16.2249C15.7707 16.473 15.4456 16.624 15.1854 16.3652L11.6848 12.8815C10.4709 13.8198 8.97529 14.3267 7.44714 14.3267C3.62134 14.3267 0.5 11.2314 0.5 7.41337C0.5 3.60616 3.6105 0.5 7.44714 0.5C11.2729 0.5 14.3943 3.59538 14.3943 7.41337C14.3943 8.98802 13.8524 10.5087 12.8661 11.7383L16.3451 15.2003ZM2.13647 7.4026C2.13647 10.3146 4.52083 12.6766 7.43624 12.6766C10.3517 12.6766 12.736 10.3146 12.736 7.4026C12.736 4.49058 10.3517 2.1286 7.43624 2.1286C4.50999 2.1286 2.13647 4.50136 2.13647 7.4026Z" fill="currentColor"></path></svg></div></form><div style="display:none;" class="search-panel"><!----><!----><!----></div></div></div><div class="mini-header-right-loading"></div></div><div class="bili-header__banner"><!----><!----><div class="header-banner__inner"><a href="//www.bilibili.com" class="inner-logo"><img class="logo-img" alt="B站 b站" width="162" height="78" src="//i0.hdslb.com/bfs/archive/c8fd97a40bf79f03e7b76cbc87236f612caef7b2.png"></a><!----></div><div class="taper-line"></div><!----></div><div class="bili-header__channel" data-v-577c5096><div class="channel-icons" data-v-577c5096><!--[--><a class="channel-icons__item" href="//t.bilibili.com" target="_blank" data-v-674f5b07><div class="icon-bg icon-bg__dynamic" data-v-674f5b07><svg width="22" height="23" viewbox="0 0 22 23" fill="none" xmlns="http://www.w3.org/2000/svg" class="icon-bg--icon" data-v-674f5b07><path d="M6.41659 15.625C3.88528 15.625 1.83325 13.7782 1.83325 11.5H10.9999C10.9999 13.7782 8.94789 15.625 6.41659 15.625Z" stroke="white" stroke-width="2" stroke-linecap="round" stroke-linejoin="round"></path><path d="M15.125 16.0827C15.125 18.614 13.2782 20.666 11 20.666L11 11.4993C13.2782 11.4993 15.125 13.5514 15.125 16.0827Z" stroke="white" stroke-width="2" stroke-linecap="round" stroke-linejoin="round"></path><path d="M6.875 6.91667C6.875 9.44797 8.72183 11.5 11 11.5L11 2.33333C8.72182 2.33333 6.875 4.38536 6.875 6.91667Z" stroke="white" stroke-width="2" stroke-linecap="round" stroke-linejoin="round"></path><path d="M15.5833 7.375C13.052 7.375 11 9.22183 11 11.5H20.1667C20.1667 9.22183 18.1146 7.375 15.5833 7.375Z" stroke="white" stroke-width="2" stroke-linecap="round" stroke-linejoin="round"></path></svg></div><!----><span class="icon-title" data-v-674f5b07>动态</span></a><a href="//www.bilibili.com/v/popular/all" target="_blank" class="channel-icons__item"><div class="icon-bg icon-bg__popular"><svg width="22" height="22" viewbox="0 0 22 22" fill="none" xmlns="http://www.w3.org/2000/svg" class="icon-bg--icon"><path fill-rule="evenodd" clip-rule="evenodd" d="M4.89054 17.272L4.89277 17.2742C6.49674 18.8782 8.66472 19.7888 10.9624 19.7888C13.2503 19.7888 15.2113 19.0539 16.6107 17.6108L16.6108 17.6108L16.6128 17.6086C18.0002 16.1345 18.7835 14.182 18.7421 12.1819C18.7852 11.3835 18.6916 9.36321 17.4088 6.75488L17.4082 6.7537C17.209 6.35523 16.8163 6.06598 16.3391 5.96993C15.8904 5.87103 15.4021 6.01997 15.061 6.35741C14.9094 6.48781 14.7796 6.61755 14.6655 6.7317L14.6637 6.73348L14.6329 6.76426C14.2107 3.35588 12.6083 1.7368 11.1654 1.00465C11.148 0.987812 11.1265 0.967972 11.1036 0.950782C11.0775 0.931205 11.0311 0.900467 10.9694 0.888912C10.2276 0.608301 9.41043 1.01168 9.1237 1.77629L9.12314 1.7778C8.50566 3.46558 7.35287 4.62281 6.16627 5.76704C4.51756 7.33121 2.75938 9.03623 2.80163 12.093C2.75906 14.055 3.54464 15.8826 4.89054 17.272ZM3.04999 13.0648C3.01092 12.7459 2.99439 12.4218 3.00168 12.0939C2.95933 9.12977 4.6531 7.47834 6.30453 5.9116C7.49017 4.76831 8.67581 3.58267 9.31098 1.84655C9.56504 1.16904 10.2849 0.830288 10.9201 1.08435C10.9624 1.08435 11.0048 1.1267 11.0471 1.16904C11.9267 1.60884 12.8853 2.39635 13.5753 3.77299C12.8853 2.39633 11.9267 1.6088 11.0471 1.16901C11.0047 1.12666 10.9624 1.08432 10.9201 1.08432C10.2849 0.830251 9.56503 1.16901 9.31097 1.84651C8.6758 3.58263 7.49016 4.76827 6.30452 5.91157C4.65309 7.47831 2.95932 9.12973 3.00166 12.0938C2.99438 12.4218 3.01092 12.7459 3.04999 13.0648ZM14.477 7.18189C14.477 7.1819 14.477 7.18192 14.477 7.18193C14.5828 7.09724 14.6887 6.99138 14.8052 6.87493C14.9216 6.75849 15.0486 6.63146 15.1968 6.50442C15.4932 6.20801 15.9167 6.08098 16.2978 6.16567C16.7212 6.25036 17.06 6.50443 17.2294 6.84318C17.3088 7.0046 17.3835 7.16371 17.4539 7.32035C17.3835 7.1637 17.3087 7.00458 17.2294 6.84314C17.06 6.50439 16.7212 6.25032 16.2978 6.16563C15.9167 6.08094 15.4932 6.20798 15.1968 6.50439C15.0486 6.63142 14.9216 6.75845 14.8051 6.87489L14.8051 6.8749C14.7557 6.92437 14.7081 6.97191 14.6617 7.01675C14.5988 7.07745 14.5379 7.13318 14.477 7.18189ZM12.6977 6.35925C12.8428 7.15476 12.8833 7.97963 12.8679 8.74864C12.8679 8.79032 12.8704 8.8315 12.8754 8.87195C12.8704 8.83151 12.8679 8.79035 12.8679 8.74867C12.8833 7.97966 12.8428 7.15478 12.6977 6.35925ZM16.7358 10.6654C16.8108 11.1478 16.8483 11.6393 16.8483 12.1362V12.1786C16.8483 13.703 16.2978 15.2274 15.2392 16.3283C14.0535 17.4293 12.5291 18.0221 10.9201 17.9374C9.1416 17.9374 7.44783 17.2175 6.21984 15.9472C5.82743 15.5548 5.50448 15.1119 5.25584 14.6331C5.50447 15.1119 5.82743 15.5548 6.21983 15.9472C7.44782 17.2175 9.14159 17.9373 10.9201 17.9373C12.5291 18.022 14.0535 17.4292 15.2392 16.3283C16.2978 15.2273 16.8483 13.7029 16.8483 12.1785V12.1362C16.8483 11.6393 16.8108 11.1478 16.7358 10.6654ZM10.9306 17.7376C12.4802 17.8192 13.9509 17.2497 15.0989 16.1856C16.1154 15.1261 16.6483 13.655 16.6483 12.1785V12.1362C16.6483 10.8624 16.3969 9.6266 15.8955 8.49474C15.2436 9.11663 14.7845 9.49093 14.4179 9.68717C14.2122 9.79725 14.0268 9.85633 13.846 9.86789C13.6644 9.8795 13.5028 9.84219 13.3473 9.78249C12.9207 9.62211 12.6679 9.20129 12.6679 8.74864V8.74464L12.6679 8.74464C12.6889 7.69735 12.6046 6.55594 12.2954 5.53554C12.01 4.59379 11.5372 3.76766 10.7904 3.20655C9.96581 4.94926 8.72521 6.18561 7.58695 7.28323L7.50836 7.35967C5.97191 8.85397 4.81321 9.98087 4.85306 12.1325L4.85313 12.1362H4.85309C4.85309 13.5239 5.38326 14.8277 6.36125 15.8057L6.36365 15.8081L6.36363 15.8082C7.55387 17.0394 9.19573 17.7374 10.9201 17.7374H10.9306L10.9306 17.7376Z" fill="#ffffff"></path></svg></div><span class="icon-title">热门</span></a><!--]--></div><div class="right-channel-container" data-v-577c5096><div class="channel-items__left"><!--[--><!--[--><a class="channel-link" href="//www.bilibili.com/anime/" style="letter-spacing:2px;" target="_blank">番剧</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/movie/" style="letter-spacing:2px;" target="_blank">电影</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/guochuang/" style="letter-spacing:2px;" target="_blank">国创</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/tv/" style="letter-spacing:2px;" target="_blank">电视剧</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/variety/" style="letter-spacing:2px;" target="_blank">综艺</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/documentary/" style="letter-spacing:2px;" target="_blank">纪录片</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/douga/" style="letter-spacing:2px;" target="_blank">动画</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/game/" style="letter-spacing:2px;" target="_blank">游戏</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/kichiku/" style="letter-spacing:2px;" target="_blank">鬼畜</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/music" style="letter-spacing:2px;" target="_blank">音乐</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/dance/" style="letter-spacing:2px;" target="_blank">舞蹈</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/cinephile" style="letter-spacing:2px;" target="_blank">影视</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/ent/" style="letter-spacing:2px;" target="_blank">娱乐</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/knowledge/" style="letter-spacing:2px;" target="_blank">知识</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/tech/" style="letter-spacing:2px;" target="_blank">科技</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/information/" style="letter-spacing:2px;" target="_blank">资讯</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/food" style="letter-spacing:2px;" target="_blank">美食</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/life" style="letter-spacing:2px;" target="_blank">生活</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/car" style="letter-spacing:2px;" target="_blank">汽车</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/fashion" style="letter-spacing:2px;" target="_blank">时尚</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/sports" style="letter-spacing:2px;" target="_blank">运动</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/animal" style="letter-spacing:2px;" target="_blank">动物圈</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/life/daily/?tag=530003" style="letter-spacing:0px;" target="_blank">VLOG</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/life/funny" style="letter-spacing:2px;" target="_blank">搞笑</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/game/stand_alone" style="letter-spacing:0px;" target="_blank">单机游戏</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/v/virtual" style="letter-spacing:0px;" target="_blank">虚拟UP主</a><!----><!--]--><!--[--><a class="channel-link" href="//love.bilibili.com" style="letter-spacing:2px;" target="_blank">公益</a><!----><!--]--><!--[--><a class="channel-link" href="//www.bilibili.com/mooc" style="letter-spacing:2px;" target="_blank">公开课</a><!----><!--]--><!--]--><!--[--><div id="channel-entry-more" class="channel-entry-more__link"><span>更多</span><svg width="10" height="10" viewbox="0 0 9 9" fill="none" xmlns="http://www.w3.org/2000/svg" class="channel-entry-more__link--arrow"><path fill-rule="evenodd" clip-rule="evenodd" d="M7.50588 3.40623C7.40825 3.3086 7.24996 3.3086 7.15232 3.40623L4.41244 6.14612L1.67255 3.40623C1.57491 3.3086 1.41662 3.3086 1.31899 3.40623C1.22136 3.50386 1.22136 3.66215 1.31899 3.75978L4.11781 6.5586C4.28053 6.72132 4.54434 6.72132 4.70706 6.5586L7.50588 3.75978C7.60351 3.66215 7.60351 3.50386 7.50588 3.40623Z" fill="currentColor"></path><path d="M7.15232 3.40623L7.50588 3.75978L7.50588 3.75978L7.15232 3.40623ZM7.50588 3.40623L7.15232 3.75978L7.15233 3.75978L7.50588 3.40623ZM4.41244 6.14612L4.05888 6.49967C4.15265 6.59344 4.27983 6.64612 4.41244 6.64612C4.54504 6.64612 4.67222 6.59344 4.76599 6.49967L4.41244 6.14612ZM1.67255 3.40623L2.0261 3.05268L2.0261 3.05268L1.67255 3.40623ZM1.31899 3.40623L0.965439 3.05268L0.965439 3.05268L1.31899 3.40623ZM1.31899 3.75978L1.67255 3.40623V3.40623L1.31899 3.75978ZM4.11781 6.5586L3.76425 6.91215L4.11781 6.5586ZM4.70706 6.5586L4.35351 6.20505L4.70706 6.5586ZM7.50588 3.75978L7.15233 3.40623L7.15232 3.40623L7.50588 3.75978ZM7.50588 3.75978C7.40825 3.85742 7.24996 3.85742 7.15232 3.75978L7.85943 3.05268C7.56654 2.75978 7.09166 2.75978 6.79877 3.05268L7.50588 3.75978ZM4.76599 6.49967L7.50588 3.75978L6.79877 3.05268L4.05888 5.79257L4.76599 6.49967ZM1.31899 3.75978L4.05888 6.49967L4.76599 5.79257L2.0261 3.05268L1.31899 3.75978ZM1.67254 3.75979C1.57491 3.85742 1.41662 3.85742 1.31899 3.75979L2.0261 3.05268C1.73321 2.75978 1.25833 2.75978 0.965439 3.05268L1.67254 3.75979ZM1.67255 3.40623C1.77018 3.50386 1.77018 3.66215 1.67255 3.75978L0.965439 3.05268C0.672546 3.34557 0.672546 3.82044 0.965439 4.11334L1.67255 3.40623ZM4.47136 6.20505L1.67255 3.40623L0.965439 4.11334L3.76425 6.91215L4.47136 6.20505ZM4.35351 6.20505C4.38605 6.1725 4.43882 6.1725 4.47136 6.20505L3.76425 6.91215C4.12223 7.27013 4.70264 7.27013 5.06062 6.91215L4.35351 6.20505ZM7.15232 3.40623L4.35351 6.20505L5.06062 6.91215L7.85943 4.11334L7.15232 3.40623ZM7.15233 3.75978C7.05469 3.66215 7.05469 3.50386 7.15233 3.40623L7.85943 4.11334C8.15233 3.82045 8.15233 3.34557 7.85943 3.05268L7.15233 3.75978Z" fill="currentColor"></path></svg></div><!----><!--]--></div><div class="channel-items__right"><!--[--><!--[--><a class="channel-link__right" href="//www.bilibili.com/read/home" style="letter-spacing:2px;" target="_blank"><svg t="1642646834655" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="4061" width="200" height="200"><path d="M810.6496 153.6C843.6736 153.6 870.4 180.3264 870.4 213.3504v597.2992c0 33.024-26.7264 59.7504-59.7504 59.7504H213.3504A59.7504 59.7504 0 0 1 153.6 810.6496V213.3504C153.6 180.3264 180.3264 153.6 213.3504 153.6z m-332.8 460.8H341.3504a34.1504 34.1504 0 0 0 0 68.2496h136.4992a34.1504 34.1504 0 1 0 0-68.2496z m204.8-136.6016H341.3504a34.1504 34.1504 0 0 0 0 68.2496h341.2992a34.1504 34.1504 0 0 0 0-68.2496z m0-136.3968H341.3504a34.1504 34.1504 0 0 0 0 68.2496h341.2992a34.1504 34.1504 0 1 0 0-68.2496z" p-id="4062"></path></svg><span>专栏</span></a><!----><!--]--><!--[--><a class="channel-link__right" href="//live.bilibili.com" style="letter-spacing:2px;" target="_blank"><svg t="1642646710703" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="3158" width="200" height="200"><path d="M682.6496 204.8512c35.4816 0 64.6656 27.136 67.9424 61.696l0.3072 6.6048V358.4l81.92-61.44a34.2016 34.2016 0 0 1 53.248 17.408l1.024 4.7616 0.3584 5.12v392.5504a34.1504 34.1504 0 0 1-50.2784 30.1056l-4.352-2.7648-81.92-61.4912v68.3008c0 33.1264-23.552 60.7232-54.8352 66.9696l-6.8608 1.024-6.5536 0.256H204.8a68.2496 68.2496 0 0 1-67.9936-61.696l-0.3072-6.5536V273.152c0-35.4816 27.136-64.6656 61.696-67.9936L204.8 204.8512h477.8496zM385.3824 389.12a34.1504 34.1504 0 0 0-34.0992 34.1504v179.6096a34.1504 34.1504 0 0 0 53.0432 28.416l134.7584-89.8048a34.1504 34.1504 0 0 0 0-56.832L404.3264 394.8544a34.1504 34.1504 0 0 0-18.944-5.7344z" p-id="3159"></path></svg><span>直播</span></a><!----><!--]--><!--[--><a class="channel-link__right" href="//www.bilibili.com/blackboard/activity-list.html?" style="letter-spacing:2px;" target="_blank"><svg t="1642646844599" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="4188" width="200" height="200"><path d="M772.4544 229.2736l2.048 6.4512 87.2448 283.136c8.8576 33.1264-10.24 66.56-41.984 78.4384l-6.5536 2.048-118.1696 31.744a32.768 32.768 0 0 1-8.192 1.0752l-4.096-0.2048-124.672-14.6432-193.3824 51.8144 36.6592 136.704a49.152 49.152 0 0 1-93.184 30.8736l-1.792-5.4272L155.2896 267.264a49.152 49.152 0 0 1 93.184-30.8736l1.792 5.4272 4.096 15.36 188.928-50.6368a32.768 32.768 0 0 1 8.1408-1.0752l4.096 0.2048 124.5184 14.592 112.1792-30.0544c33.4336-8.96 68.1984 7.7824 80.2304 39.0144z" p-id="4189"></path></svg><span>活动</span></a><!----><!--]--><!--[--><a class="channel-link__right" href="//www.bilibili.com/cheese/?csource=common_hp_channelclass_icon" style="letter-spacing:2px;" target="_blank"><svg t="1642669966795" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="2862" width="200" height="200"><path d="M749.2096 168.96a102.4 102.4 0 0 1 102.2464 96.3584l0.1536 6.0416v477.8496a102.4 102.4 0 0 1-96.3584 102.2464l-6.0416 0.1536H271.36a102.4 102.4 0 0 1-102.2464-96.3584l-0.1536-6.0416V271.36a102.4 102.4 0 0 1 96.3584-102.2464L271.36 168.96h477.8496z m-69.9392 385.4848a34.1504 34.1504 0 0 0-48.2816 0 170.6496 170.6496 0 0 1-241.3568 0 34.1504 34.1504 0 1 0-48.2816 48.2304 238.9504 238.9504 0 0 0 337.92 0 34.1504 34.1504 0 0 0 0-48.2304zM322.56 339.6608a51.2 51.2 0 0 0-51.2 51.2v34.1504a51.2 51.2 0 1 0 102.4 0v-34.1504a51.2 51.2 0 0 0-51.2-51.2z m375.4496 0a51.2 51.2 0 0 0-51.2 51.2v34.1504a51.2 51.2 0 1 0 102.4 0v-34.1504a51.2 51.2 0 0 0-51.2-51.2z" p-id="2863"></path></svg><span>课堂</span></a><!----><!--]--><!--[--><a class="channel-link__right" href="https://www.bilibili.com/blackboard/activity-5zJxM3spoS.html" style="letter-spacing:0px;" target="_blank"><svg t="1642670011510" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="3116" width="200" height="200"><path d="M836.3008 170.6496c17.1008 0 31.2832 12.6464 33.7408 29.0816L870.4 204.8v316.16a34.1504 34.1504 0 0 1-29.0816 33.792l-5.0176 0.3584h-102.4v195.7888a34.1504 34.1504 0 0 1-29.1328 33.792l-5.0176 0.3584H386.7648l-127.3344 95.5392a34.2016 34.2016 0 0 1-53.248-17.3568l-1.024-4.8128-0.3584-5.12-0.0512-68.3008H153.6a34.1504 34.1504 0 0 1-32.6656-24.2176l-1.0752-4.8128-0.4096-5.0688v-409.6c0-17.152 12.6464-31.3344 29.0816-33.792L153.6 307.2h174.2336V204.8c0-17.152 12.6464-31.3344 29.1328-33.792l5.0176-0.3584h474.3168z m-477.9008 409.6H256l-5.0688 0.4096a34.1504 34.1504 0 0 0 0 67.4816l5.0688 0.4096h102.4l5.0688-0.4096A34.1504 34.1504 0 0 0 358.4 580.2496z m102.4-136.4992H256l-5.0688 0.4096a34.1504 34.1504 0 0 0 0 67.4816l5.0688 0.4096h204.8l5.0688-0.4096A34.1504 34.1504 0 0 0 460.8 443.7504z m341.2992-204.8512h-406.016v68.2496h303.616c17.152 0 31.3856 12.6464 33.792 29.1328l0.3584 5.0176v145.4592l68.2496 0.0512V238.8992z" p-id="3117"></path></svg><span>社区中心</span></a><!----><!--]--><!--[--><a class="channel-link__right" href="//music.bilibili.com/pc/music-center/" style="letter-spacing:0px;" target="_blank"><svg t="1642669999866" class="icon side-icon" viewbox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="2989" width="200" height="200"><path d="M783.36 221.8496a102.4 102.4 0 0 1 102.0928 94.7712l0.3072 7.68v409.6a102.4 102.4 0 0 1-94.72 102.0928l-7.68 0.256H237.2096a102.4 102.4 0 0 1-102.0928-94.72l-0.3072-7.68v-409.6A102.4 102.4 0 0 1 229.5808 222.208l7.68-0.3072H783.36z m-155.5968 81.408a34.1504 34.1504 0 0 0-50.7904 23.6032l-54.1696 203.3152a128 128 0 1 0-108.288 220.8256l6.7584 1.024a128 128 0 0 0 141.5168-104.8576l71.7824-253.7984 47.4624 35.4816 3.2768 2.2016a34.1504 34.1504 0 0 0 37.5808-56.832l-91.8528-68.7616z" p-id="2990"></path></svg><span>新歌热榜</span></a><!----><!--]--><!--]--></div></div></div><!----></div><!----><!----><!--]--><!----><!----><main class="bili-feed4-layout"><div class="fixed-channel-shim"></div><div class="feed2"><!--[--><div class="recommended-container_floor-aside" data-v-22213b9e><div class="container is-version8" data-v-22213b9e><div class="recommended-swipe grid-anchor" data-loc-id="4694" style="--cover-radio:56.25%;" data-v-22213b9e><div class="recommended-swipe-core"><div class="recommended-swipe-shim"><div class="bili-video-card" style="--cover-radio:56.25%;" data-report><div class="bili-video-card__skeleton"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><!----></div><div class="bili-video-card" style="--cover-radio:56.25%;" data-report><div class="bili-video-card__skeleton"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><!----></div><div class="shim-card"></div><div class="shim-card"></div></div><div class="recommended-swipe-body"><!--[--><!--[--><!--]--><!--[--><!--[--><div class="carousel-area"><div class="carousel" data-v-3f80e0b0><div class="carousel-container" style="overflow-x:hidden;height:;overflow-y:;width:100%;" data-v-3f80e0b0><!--[--><!--[--><!----><!----><!----><!----><!----><!----><!----><!----><!----><!--]--><!--]--><div style="" class="carousel-transform clearfix" data-v-3f80e0b0><!--[--><!--]--></div><div class="carousel-footer" data-v-3f80e0b0><!--[--><div class="carousel-mask" style="background-color:#463e50;"></div><div class="carousel-tool not-gray" data-gray="66" style="color:white;"><a href="https://live.bilibili.com/6?live_from=81001" target="_blank"><span>正在直播MSI:TL vs TES!</span></a><ul class="not-gray"><!--[--><li class="is-active"><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><li class=""><div class="before"></div><div class="after"></div></li><!--]--></ul></div><div class="buttons not-gray"><!----><div><button><svg style="transform:rotate(180deg);"><use xlink:href="#widget-arrow"></use></svg></button><button><svg><use xlink:href="#widget-arrow"></use></svg></button></div></div><!--]--></div></div></div></div><!--]--><!--]--><!--[--><!--]--><!----><!--[--><!----><!--]--><!--]--></div></div></div><!--[--><!--[--><!--[--><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.1-1-1.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1jx421X7zH" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/26d3051cf0e42ecec582c0cc7d71c4ed04be561b.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/26d3051cf0e42ecec582c0cc7d71c4ed04be561b.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/26d3051cf0e42ecec582c0cc7d71c4ed04be561b.jpg@672w_378h_1c_!web-home-common-cover" alt="10分钟速通计算机网络 每个开发者都具备的计算机常识" loading="eager" onload onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">23万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">502</span></span></div><span class="bili-video-card__stats__duration">10:38</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="10分钟速通计算机网络 每个开发者都具备的计算机常识"><a href="https://www.bilibili.com/video/BV1jx421X7zH" target="_blank">10分钟速通计算机网络 每个开发者都具备的计算机常识</a></h3><div class="bili-video-card__info--bottom"><div class="bili-video-card__info--icon-text">1万点赞</div><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/482867012" target="_blank"><!----><span class="bili-video-card__info--author" title="吴悠讲编程">吴悠讲编程</span><span class="bili-video-card__info--date">· 3-26</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.1-2-2.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1Vx4y1a7VB" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/0ea6e751ccaa3a5311261f3081922a48874ffe8c.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/0ea6e751ccaa3a5311261f3081922a48874ffe8c.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/0ea6e751ccaa3a5311261f3081922a48874ffe8c.jpg@672w_378h_1c_!web-home-common-cover" alt="当我来到世界尽头" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">220.3万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">7286</span></span></div><span class="bili-video-card__stats__duration">18:20</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="当我来到世界尽头"><a href="https://www.bilibili.com/video/BV1Vx4y1a7VB" target="_blank">当我来到世界尽头</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/3816626" target="_blank"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="currentColor" class="bili-video-card__info--owner__up"><!--[--><!--]--></svg><span class="bili-video-card__info--author" title="Linksphotograph">Linksphotograph</span><span class="bili-video-card__info--date">· 4-13</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.1-3-3.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1hT421C7PP" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/3419a591aeef4a53ea66e754a2f535e1d0daac85.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/3419a591aeef4a53ea66e754a2f535e1d0daac85.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/3419a591aeef4a53ea66e754a2f535e1d0daac85.jpg@672w_378h_1c_!web-home-common-cover" alt="K8S即职场(一)" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">336</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">0</span></span></div><span class="bili-video-card__stats__duration">11:06</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="K8S即职场(一)"><a href="https://www.bilibili.com/video/BV1hT421C7PP" target="_blank">K8S即职场(一)</a></h3><div class="bili-video-card__info--bottom"><div class="bili-video-card__info--icon-text">已关注</div><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/12188390" target="_blank"><!----><span class="bili-video-card__info--author" title="佚名运维">佚名运维</span><span class="bili-video-card__info--date">· 5-1</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.2-1-4.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1sE421M77B" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/bf0fe03778c678ba9760aa8b983c66f3c2223668.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/bf0fe03778c678ba9760aa8b983c66f3c2223668.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/bf0fe03778c678ba9760aa8b983c66f3c2223668.jpg@672w_378h_1c_!web-home-common-cover" alt="突袭100个同事键盘,每个都好想要!!!" loading="eager" onload onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">279.6万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">3419</span></span></div><span class="bili-video-card__stats__duration">13:21</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="突袭100个同事键盘,每个都好想要!!!"><a href="https://www.bilibili.com/video/BV1sE421M77B" target="_blank">突袭100个同事键盘,每个都好想要!!!</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/487425891" target="_blank"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="currentColor" class="bili-video-card__info--owner__up"><!--[--><!--]--></svg><span class="bili-video-card__info--author" title="可以去你家嘛">可以去你家嘛</span><span class="bili-video-card__info--date">· 4-19</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.2-2-5.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV17m411U7cC" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/c7192b303df325ee36a63b856ff90d7e83ac7e6d.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/c7192b303df325ee36a63b856ff90d7e83ac7e6d.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/c7192b303df325ee36a63b856ff90d7e83ac7e6d.jpg@672w_378h_1c_!web-home-common-cover" alt="30分钟Shell光速入门教程" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">5.7万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">48</span></span></div><span class="bili-video-card__stats__duration">24:15</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="30分钟Shell光速入门教程"><a href="https://www.bilibili.com/video/BV17m411U7cC" target="_blank">30分钟Shell光速入门教程</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/102438649" target="_blank"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="currentColor" class="bili-video-card__info--owner__up"><!--[--><!--]--></svg><span class="bili-video-card__info--author" title="GeekHour">GeekHour</span><span class="bili-video-card__info--date">· 4-20</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.2-3-6.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1cH4y1P7AT" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/49bbb6f72877f1336f46b9853bd09b2fd22f5ca3.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/49bbb6f72877f1336f46b9853bd09b2fd22f5ca3.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/49bbb6f72877f1336f46b9853bd09b2fd22f5ca3.jpg@672w_378h_1c_!web-home-common-cover" alt="【2024安卓开发】Android转行有哪些最优选择?需要具备哪些技能?" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">6650</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">48</span></span></div><span class="bili-video-card__stats__duration">17:48</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="【2024安卓开发】Android转行有哪些最优选择?需要具备哪些技能?"><a href="https://www.bilibili.com/video/BV1cH4y1P7AT" target="_blank">【2024安卓开发】Android转行有哪些最优选择?需要具备哪些技能?</a></h3><div class="bili-video-card__info--bottom"><div class="bili-video-card__info--icon-text">已关注</div><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/474380680" target="_blank"><!----><span class="bili-video-card__info--author" title="Android架构解析">Android架构解析</span><span class="bili-video-card__info--date">· 4-25</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd" style="--cover-radio:56.25%;" data-report="tianma.3-1-7.click" data-v-22213b9e><!----><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://ht.nextclass.com/CMS/prod/5264/288/home.html?mantisSiteId=7188&track_id=pbaes.Z4e0-VNVpS3ADLCsn_QpkAdkcSOplRvCKp2Mv860iA9bLHYhWOvRXIJzh1Jxt8-NcLUtHNsK_eVvvK1qePEjOfTy4NXcLvcuCocvQuCLX4Y3xVsb2E8WjCuNlGwCwCeOvSnCasX9B4CakM9-fW9MacJcTKHeSv0VPG3oEuZ77COEKB8wAnC-vGrrq-ge3v3i" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/sycp/creative_img/202404/d1060048b5db15af37fe8f3d673ed0e4.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/sycp/creative_img/202404/d1060048b5db15af37fe8f3d673ed0e4.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/sycp/creative_img/202404/d1060048b5db15af37fe8f3d673ed0e4.jpg@672w_378h_1c_!web-home-common-cover" alt="别拉不下面子,你真应该抓住风口学AI搞钱" loading="eager" onload onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><!----></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!----><h3 class="bili-video-card__info--tit" title="别拉不下面子,你真应该抓住风口学AI搞钱"><a href="https://ht.nextclass.com/CMS/prod/5264/288/home.html?mantisSiteId=7188&track_id=pbaes.Z4e0-VNVpS3ADLCsn_QpkAdkcSOplRvCKp2Mv860iA9bLHYhWOvRXIJzh1Jxt8-NcLUtHNsK_eVvvK1qePEjOfTy4NXcLvcuCocvQuCLX4Y3xVsb2E8WjCuNlGwCwCeOvSnCasX9B4CakM9-fW9MacJcTKHeSv0VPG3oEuZ77COEKB8wAnC-vGrrq-ge3v3i" target="_blank">别拉不下面子,你真应该抓住风口学AI搞钱</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner disable-hover" href="https://ht.nextclass.com/CMS/prod/5264/288/home.html?mantisSiteId=7188&track_id=pbaes.Z4e0-VNVpS3ADLCsn_QpkAdkcSOplRvCKp2Mv860iA9bLHYhWOvRXIJzh1Jxt8-NcLUtHNsK_eVvvK1qePEjOfTy4NXcLvcuCocvQuCLX4Y3xVsb2E8WjCuNlGwCwCeOvSnCasX9B4CakM9-fW9MacJcTKHeSv0VPG3oEuZ77COEKB8wAnC-vGrrq-ge3v3i" target="_blank"><!----><svg class="bili-video-card__info--ad"><use xlink:href="#palette-ad"></use></svg><span class="bili-video-card__info--author" title="遍知教育">遍知教育</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.3-2-8.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1ox4y1B7gS" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/b1f82fd8c2b6692498487c4dbdccc9e8b9a099e2.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/b1f82fd8c2b6692498487c4dbdccc9e8b9a099e2.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/b1f82fd8c2b6692498487c4dbdccc9e8b9a099e2.jpg@672w_378h_1c_!web-home-common-cover" alt="结束12年的婚姻后,一些想对你们说的心里话" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">116.5万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">3343</span></span></div><span class="bili-video-card__stats__duration">06:58</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="结束12年的婚姻后,一些想对你们说的心里话"><a href="https://www.bilibili.com/video/BV1ox4y1B7gS" target="_blank">结束12年的婚姻后,一些想对你们说的心里话</a></h3><div class="bili-video-card__info--bottom"><div class="bili-video-card__info--icon-text">4万点赞</div><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/26385307" target="_blank"><!----><span class="bili-video-card__info--author" title="朱莉姐姐Julie">朱莉姐姐Julie</span><span class="bili-video-card__info--date">· 4-29</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.3-3-9.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV19z42167uq" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/eb6e82f102367f1a197613c0288d77975f0a93e0.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/eb6e82f102367f1a197613c0288d77975f0a93e0.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/eb6e82f102367f1a197613c0288d77975f0a93e0.jpg@672w_378h_1c_!web-home-common-cover" alt="120秒学会10种旅拍 【大师运镜】" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">47.4万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">198</span></span></div><span class="bili-video-card__stats__duration">03:53</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="120秒学会10种旅拍 【大师运镜】"><a href="https://www.bilibili.com/video/BV19z42167uq" target="_blank">120秒学会10种旅拍 【大师运镜】</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/396967836" target="_blank"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="currentColor" class="bili-video-card__info--owner__up"><!--[--><!--]--></svg><span class="bili-video-card__info--author" title="哲瀚去拍摄了">哲瀚去拍摄了</span><span class="bili-video-card__info--date">· 4-26</span></a><!--]--></div></div></div></div></div></div><div class="feed-card" data-v-22213b9e><div class="bili-video-card is-rcmd enable-no-interest" style="--cover-radio:56.25%;" data-report="tianma.3-4-10.click" data-v-22213b9e><div class="bili-video-card__skeleton hide"><div class="bili-video-card__skeleton--cover"></div><div class="bili-video-card__skeleton--info"><div class="bili-video-card__skeleton--right"><p class="bili-video-card__skeleton--text"></p><p class="bili-video-card__skeleton--text short"></p><p class="bili-video-card__skeleton--light"></p></div></div></div><!----><div class="bili-video-card__wrap __scale-wrap"><!----><a class="bili-video-card__image--link" href="https://www.bilibili.com/video/BV1Fz421C7TZ" target="_blank"><div class="bili-video-card__image __scale-player-wrap bili-video-card__image--hover"><div class="bili-video-card__image--wrap"><!----><picture class="v-img bili-video-card__cover"><!--[--><source srcset="//i2.hdslb.com/bfs/archive/5ff1572ae4eac86a217f2d80f8ed2b758649097e.jpg@672w_378h_1c_!web-home-common-cover.avif" type="image/avif"><source srcset="//i2.hdslb.com/bfs/archive/5ff1572ae4eac86a217f2d80f8ed2b758649097e.jpg@672w_378h_1c_!web-home-common-cover.webp" type="image/webp"><img src="//i2.hdslb.com/bfs/archive/5ff1572ae4eac86a217f2d80f8ed2b758649097e.jpg@672w_378h_1c_!web-home-common-cover" alt="中科院放大招了,偷偷出了4个神器!" loading="eager" onload="fsrCb()" onerror="typeof window.imgOnError === 'function' && window.imgOnError(this)"><!--]--></picture></div><div class="bili-video-card__mask"><div class="bili-video-card__stats"><div class="bili-video-card__stats--left"><!--[--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">103.7万</span></span><!--]--><span class="bili-video-card__stats--item"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="#ffffff" class="bili-video-card__stats--icon"><!--[--><!--]--></svg><span class="bili-video-card__stats--text">271</span></span></div><span class="bili-video-card__stats__duration">01:11</span></div></div></div></a><div style="" class="bili-video-card__info __scale-disable"><!--[--><!----><!--]--><div class="bili-video-card__info--right"><!--[--><div class="bili-video-card__info--no-interest" style="display:none;"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" class="bili-video-card__info--no-interest--icon" fill="currentColor"><!--[--><!--]--></svg></div><!----><!--]--><h3 class="bili-video-card__info--tit" title="中科院放大招了,偷偷出了4个神器!"><a href="https://www.bilibili.com/video/BV1Fz421C7TZ" target="_blank">中科院放大招了,偷偷出了4个神器!</a></h3><div class="bili-video-card__info--bottom"><!----><!--[--><a class="bili-video-card__info--owner" href="//space.bilibili.com/486989780" target="_blank"><svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 24 24" width="24" height="24" fill="currentColor" class="bili-video-card__info--owner__up"><!--[--><!--]--></svg><span class="bili-video-card__info--author" title="老麦的工具库">老麦的工具库</span><span class="bili-video-card__info--date">· 4-15</span></a><!--]--></div></div></div></div></div></div><!--]--><!----><!--]--><!----><!----><!--]--></div><!----><!----><!----></div><!--]--><!----></div></main><!----></div><!--]--></div><script>window.__INITIAL_DATA__=[{"request":{"url":"http:\u002F\u002Fapi.bilibili.com\u002Fx\u002Fweb-show\u002Fpage\u002Fheader?resource_id=142","config":{"preload":true,"com2co":true,"discovery":"main.web-svr.web-show","method":"GET","credentials":"include"}},"response":{"name":"","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002Fa947affc321e82798ade231ef5551b7298d90e4b.png","litpic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002Fc8fd97a40bf79f03e7b76cbc87236f612caef7b2.png","url":"","is_split_layer":1,"split_layer":"{\"version\":\"1\",\"layers\":[{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F17a1bcfacfc51f000cad0611dca32020b18db6f5.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":0,\"name\":\"23_bg\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Ff0ba9b7f8d4ec1745a08cabdf3951ceb4aa266d1.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"offset\":[2,-10]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":1,\"name\":\"22_云朵\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fbe5632d3f86228a81979b8a85ce9cf0d5df541e0.png\",\"id\":0}],\"scale\":{\"initial\":1.2},\"rotate\":{},\"translate\":{\"initial\":[250,20],\"offset\":[5,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":2,\"name\":\"21_建筑\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Ff63cf9726b73c78ececc43ff16f3336fdfc76748.png\",\"id\":0}],\"scale\":{\"initial\":1.1},\"rotate\":{},\"translate\":{\"initial\":[300,30],\"offset\":[30,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":3,\"name\":\"20_右侧远屋顶\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F2c32dd208cb8f317ac78e03c78da5cd04b9a1410.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[12,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":4,\"name\":\"19_指示牌\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fe04d0fbaaf67bdb0de7c40dca04180a9c1defa0a.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[18,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":5,\"name\":\"18_大猫背后植物\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fd5113ee4aaca71d7e7570a45b1e541efc0deca71.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[30,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":6,\"name\":\"!17_猫身体\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fae0543610dd9b3d0903cec7a6982200691dce1b5.png\",\"id\":0}],\"scale\":{\"offsetCurve\":[1,0,0,0]},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[32,6],\"offsetCurve\":[0.1975,0.9665,0.6595,-0.48]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":24,\"name\":\"17_猫眼珠\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F6d9f792b3458e0b6f8647f7ad3958b1c1438d50e.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[30,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":25,\"name\":\"17_猫镂空\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Ff3945f0ed928e45fb58c8a1edb07358ec719c8df.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[40,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":8,\"name\":\"15_右边小猫\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fba22577d90164e589f87f9073d56953ff3e30088.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[55,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":9,\"name\":\"14_电话亭\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fd6ef89533fed72dfde53009ac2aab66009ab545a.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[100,15],\"offset\":[30,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":10,\"name\":\"13_远电线杆\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F8cacfce7b1f44f707836fa4fb68444a9c7202d63.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[60,1]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":11,\"name\":\"12_中间花田\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fff63f10698f5f0a9e9083d90c6f32de5269801d4.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,10],\"offset\":[80,1]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":12,\"name\":\"11_山坡地板\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F5630bebd1068fa6c46eaea4ffa9b004f882d7d33.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[80,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":13,\"name\":\"10_前景电线杆\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fa7ead379e7a6653cd70f24e8556ce336702abb3a.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[80,4]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":16,\"name\":\"07_33\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F06336184ba84f89890f50e867012c05914219947.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[120,5]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":17,\"name\":\"06_22\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fddc58cd92df71ada0be9bad00b2139a34872ef94.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[-100,15],\"offset\":[180,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":14,\"name\":\"09_左前小花\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F996a5656d3a31738f79b67d94ea0b654fba169ac.png\",\"id\":0}],\"scale\":{\"initial\":0.9},\"rotate\":{},\"translate\":{\"initial\":[-100,0],\"offset\":[300,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":15,\"name\":\"08_左前大花\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F905fbc85df462f16c3fe0b83f0e5814696818a56.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"offset\":[120,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":18,\"name\":\"05_右前小花\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F4d37acea06841ace858f27cab3a5596d9fdd8354.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"offset\":[150,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":19,\"name\":\"04_右前大花\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fc01047a141434bb40b03acfc32a5b1cb6d6aaf88.webm\",\"id\":0}],\"scale\":{},\"rotate\":{\"offset\":30,\"offsetCurve\":[1,0.0040000000000000036,0,0.565]},\"translate\":{\"initial\":[-245,15],\"offset\":[100,0],\"offsetCurve\":[0.18650000000000003,1.4505,0.3075,-0.4690000000000001]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":23,\"name\":\"03_蝴蝶动\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002Fd4d4569741806055f36c4d9140bdd7069a50ec09.png\",\"id\":0}],\"scale\":{\"initial\":1.1},\"rotate\":{},\"translate\":{\"offset\":[200,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":21,\"name\":\"02_右边紫花\"},{\"resources\":[{\"src\":\"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fvc\u002F2dd4a5f8aee1829bcdae687052853b8947a5d2f6.png\",\"id\":0}],\"scale\":{},\"rotate\":{},\"translate\":{\"initial\":[0,15],\"offset\":[200,0]},\"blur\":{},\"opacity\":{\"wrap\":\"clamp\"},\"id\":22,\"name\":\"01_乱飞\"}]}","request_id":"1715073695"}},{"request":{"url":"http:\u002F\u002Fapi.bilibili.com\u002Fx\u002Fweb-show\u002Fres\u002Flocs?pf=0&ids=4694","config":{"preload":true,"com2co":true,"encWbi":true,"discovery":"main.web-svr.web-show","method":"GET","credentials":"include"}},"response":{"4694":[{"id":1502935,"contract_id":"","res_id":4694,"asg_id":1476377,"pos_num":1,"name":"正在直播MSI:TL vs TES!","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F1e10146ca96f2700fe6c47bdb0d71547757c07e4.png","litpic":"","url":"https:\u002F\u002Flive.bilibili.com\u002F6","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695","src_id":4695,"area":1,"is_ad_loc":false,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715072400,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"#463e50","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502596,"contract_id":"","res_id":4695,"asg_id":1476052,"pos_num":2,"name":"AI时代,聊聊读书这件小事~","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F1b35eb8856f928ee03d724817878265747b9a10c.jpg","litpic":"","url":"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1fx4y1z7Hd\u002F?spm_id_from=333.337.search-card.all.click&vd_source=8fb566ae9aefe8fe5e5e8711b46b7964","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695305q172a27a44a148q3504","src_id":4696,"area":1,"is_ad_loc":true,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715011200,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"#92767b","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1499345,"contract_id":"","res_id":4694,"asg_id":1473071,"pos_num":3,"name":"投稿出行瓜分3W奖金!","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002Fb76624e1e282b21db2b19e512ab6d1c8312494d5.jpg","litpic":"#7778a0","url":"https:\u002F\u002Fwww.bilibili.com\u002Fblackboard\u002Factivity-8T9yawlpPg.html","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695305q172a27a44a148q3504","src_id":4697,"area":1,"is_ad_loc":true,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715011200,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502571,"contract_id":"","res_id":4694,"asg_id":1476027,"pos_num":4,"name":"照这样下去,她会疯的","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F0c6a098b69886f447b2061bd8cc10a2f3364df0c.png","litpic":"#8b2a46","url":"https:\u002F\u002Fwww.bilibili.com\u002Fbangumi\u002Fplay\u002Fep817476","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695","src_id":4698,"area":1,"is_ad_loc":false,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715050800,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502274,"contract_id":"","res_id":4694,"asg_id":1475732,"pos_num":5,"name":"一曲东风破,忆起旧时光","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F2e357de125e55ac74243f1f1ff9548278fd295aa.png","litpic":"#c3acb9","url":"https:\u002F\u002Fwww.bilibili.com\u002Fbangumi\u002Fplay\u002Fep820442","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695","src_id":4699,"area":1,"is_ad_loc":false,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715050800,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502205,"contract_id":"","res_id":4694,"asg_id":1475666,"pos_num":6,"name":"圆满完结!登上莫雷诺山,看太阳升起…","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F6d6696a4fff580b3f849abc2bae0908892e2b787.png","litpic":"#30211a","url":"https:\u002F\u002Fwww.bilibili.com\u002Fbangumi\u002Fplay\u002Fep818986","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695","src_id":4700,"area":1,"is_ad_loc":false,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1714996800,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1499461,"contract_id":"","res_id":4694,"asg_id":1473179,"pos_num":7,"name":"我 很 精 神 啊","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F354d1b4f7b1e752a3a3ee73004ce961a04d74031.png","litpic":"#634861","url":"https:\u002F\u002Fwww.bilibili.com\u002Fblackboard\u002Fera\u002FUSUDVlaSwJTwexBa.html?msource=shoujiao","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695305q172a27a44a148q3504","src_id":4701,"area":1,"is_ad_loc":true,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715011200,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502657,"contract_id":"","res_id":4694,"asg_id":1476112,"pos_num":8,"name":"抽卡、积累战斗力,更多玩法等你解锁!","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F6abe453c5d805dde094ce244dc63d371c6daffbb.jpg","litpic":"#5f6596","url":"https:\u002F\u002Fwww.bilibili.com\u002Fblackboard\u002Fera\u002FNSZJkjms68hZiueI.html","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695305q172a27a44a148q3504","src_id":4702,"area":1,"is_ad_loc":true,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715011200,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502831,"contract_id":"","res_id":4694,"asg_id":1476277,"pos_num":9,"name":"华晨宇日出演唱会《向阳而生》","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002F4820131d8d8598ec2017f08dbca8b4343be9376a.jpg","litpic":"#5b3221","url":"http:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1AD421K7Ha","style":0,"archive":{"aid":1504000822,"videos":1,"tid":29,"tname":"音乐现场","copyright":1,"pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002F9675d9769a9faab06d38221d8973d4ed4e98c460.jpg","title":"华晨宇看日出演唱会15分钟《向阳而生》(日出live版)","pubdate":1714829779,"ctime":1714829779,"desc":"星辰退却,天边渐白,金色光芒洒满大地,照亮彼此的脸庞,共看日出绮丽景象,迎接绚烂与希望。\n华晨宇看日出演唱会15分钟《向阳而生》(日出live版)官摄上线!","state":0,"duration":947,"mission_id":4012023,"rights":{"bp":0,"elec":0,"download":0,"movie":0,"pay":0,"hd5":0,"no_reprint":1,"autoplay":1,"ugc_pay":0,"is_cooperation":1,"ugc_pay_preview":0,"no_background":0,"arc_pay":0,"pay_free_watch":0},"owner":{"mid":477569206,"name":"华晨宇工作室","face":"https:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Fface\u002F1bfa31a8b8f13a92b00e5482facc4218e607200f.jpg"},"stat":{"aid":1504000822,"view":742563,"danmaku":16080,"reply":13571,"favorite":47726,"coin":82881,"share":27813,"now_rank":0,"his_rank":12,"like":67913,"dislike":0,"vt":0,"vv":742563},"dynamic":"","cid":1531005824,"dimension":{"width":1920,"height":1080,"rotate":0},"short_link_v2":"https:\u002F\u002Fb23.tv\u002FBV1AD421K7Ha","first_frame":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fstoryff\u002Fn240504sa3rtddyedzq8df3he9ks9d0l_firsti.jpg","pub_location":"山东","bvid":"BV1AD421K7Ha","enable_vt":0},"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695305q172a27a44a148q3504","src_id":4703,"area":1,"is_ad_loc":true,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715054400,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"},{"id":1502381,"contract_id":"","res_id":4694,"asg_id":1475839,"pos_num":10,"name":"相信是最真挚的情感","pic":"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbanner\u002Fe55704a9c835dca6d54c391e61976df70d78326a.png","litpic":"#5d4c53","url":"https:\u002F\u002Fwww.bilibili.com\u002Fbangumi\u002Fplay\u002Fep823184","style":0,"agency":"","label":"","intro":"","creative_type":0,"request_id":"1715073695","src_id":4704,"area":1,"is_ad_loc":false,"ad_cb":"","title":"","server_type":0,"cm_mark":0,"stime":1715050800,"mid":"1959817098","activity_type":0,"epid":0,"season":null,"room":null,"sub_title":"","ad_desc":"","adver_name":"","null_frame":false,"pic_main_color":"","card_type":0,"business_mark":null,"inline":{"inline_use_same":1,"inline_type":0,"inline_url":"","inline_barrage_switch":1},"operater":"manager_banner_10948"}]}}]</script><script type="text/javascript">window.__pinia=(function(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z,A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,_,$,aa,ab,ac,ad,ae,af,ag,ah,ai,aj,ak,al,am,an,ao,ap,aq,ar,as,at,au,av,aw,ax,ay,az,aA,aB,aC,aD,aE,aF,aG,aH,aI,aJ,aK,aL,aM,aN,aO,aP,aQ,aR,aS,aT,aU,aV,aW,aX,aY,aZ,a_,a$,ba,bb,bc,bd,be,bf,bg,bh,bi,bj,bk,bl,bm,bn,bo,bp,bq,br,bs,bt,bu,bv,bw,bx,by,bz,bA,bB,bC,bD,bE,bF,bG,bH,bI,bJ,bK,bL,bM,bN,bO,bP,bQ,bR,bS,bT,bU,bV,bW,bX,bY,bZ,b_,b$,ca,cb,cc,cd,ce,cf,cg,ch,ci,cj,ck,cl,cm,cn,co,cp,cq,cr,cs,ct,cu,cv,cw,cx,cy,cz,cA,cB,cC,cD,cE,cF,cG,cH,cI,cJ,cK,cL,cM,cN,cO,cP,cQ,cR,cS,cT,cU,cV,cW,cX,cY,cZ,c_,c$,da,db,dc,dd){ad.freshIdx=a;ad.id=B;ad.reportId="av_n_1752410818";ae.freshIdx=a;ae.id=C;ae.reportId="av_n_1003064936";af.freshIdx=a;af.id=D;af.reportId="av_n_1703793439";ag.freshIdx=a;ag.id=E;ag.reportId="av_n_1653327492";ah.freshIdx=a;ah.id=F;ah.reportId="av_n_1903342555";ai.freshIdx=a;ai.id=G;ai.reportId="av_n_1053704434";aj.freshIdx=a;aj.id=N;aj.reportId="ad_n_5614";ak.freshIdx=a;ak.id=H;ak.reportId="av_n_1003850291";al.freshIdx=a;al.id=I;al.reportId="av_n_1353614413";am.freshIdx=a;am.id=J;am.reportId="av_n_1353009029";bL.bg_border_color=W;bL.bg_color=d;bL.bg_color_night=d;bL.border_color=W;bL.border_color_night=bM;bL.img_height=a;bL.img_url=d;bL.img_width=a;bL.text="广告";bL.text_color=W;bL.text_color_night=bM;bL.type=t;return {index:{enableAvif:e,bmgDefDomain:"i2.hdslb.com",homeVersion:ac,smallest:f,xs_sm:f,xs:f,sm:f,md:f,lg:f,xl:f,xxl:f,popWindowVersion:h,experimentConstants:{previewTipCountingSecond:b,previewCountingSecond:q,nanoVersionHash:"a8c001e3",nanoVersionPipHash:"71a769ad",nanoVersionPcdnHash:"57abf745",tianma_banner_inline_V0:A,tianma_banner_inline_V1:M},themeSwitchVersion:"CLOSE",tianmaBannerInlineVersion:"CONTROL",exitFeedBtnVersion:"HIDE",forceToFeedVersion:"GO",enableWebPushVersion:"DISABLE"},feed:{feedReqCardList:[ad,ae,af,ag,ah,ai,aj,ak,al,am],currentReqList:[ad,ae,af,ag,ah,ai,aj,ak,al,am],homeVersion:ac,refreshed:f,hasMoreHeadRecommend:e,banner_card_cur_idx:a,brush:{dropDown:a,refresh:A},fresh_type:a,timestamp:1715073695107,fresh_idx_1h:a,fresh_idx:a,fetch_row:b,data:{loading:f,ad:[],banner_card:[],recommend:{item:[{id:B,bvid:an,cid:ao,goto:l,uri:ap,pic:O,pic_4_3:aq,title:ar,duration:as,pubdate:at,owner:{mid:au,name:av,face:aw},stat:{view:ax,like:ay,danmaku:az,vt:a},av_feature:c,is_followed:a,rcmd_reason:{content:aA,reason_type:o},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:C,bvid:aB,cid:aC,goto:l,uri:aD,pic:v,pic_4_3:v,title:aE,duration:aF,pubdate:aG,owner:{mid:aH,name:aI,face:aJ},stat:{view:aK,like:aL,danmaku:aM,vt:a},av_feature:c,is_followed:a,rcmd_reason:{reason_type:a},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:D,bvid:aN,cid:aO,goto:l,uri:aP,pic:w,pic_4_3:w,title:aQ,duration:aR,pubdate:aS,owner:{mid:aT,name:aU,face:aV},stat:{view:aW,like:P,danmaku:a,vt:a},av_feature:c,is_followed:b,rcmd_reason:{reason_type:b},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:E,bvid:aX,cid:aY,goto:l,uri:aZ,pic:Q,pic_4_3:a_,title:a$,duration:ba,pubdate:bb,owner:{mid:bc,name:bd,face:be},stat:{view:bf,like:bg,danmaku:bh,vt:a},av_feature:c,is_followed:a,rcmd_reason:{reason_type:a},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:F,bvid:bi,cid:bj,goto:l,uri:bk,pic:R,pic_4_3:bl,title:bm,duration:bn,pubdate:bo,owner:{mid:bp,name:bq,face:br},stat:{view:bs,like:bt,danmaku:K,vt:a},av_feature:c,is_followed:a,rcmd_reason:{reason_type:a},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:G,bvid:bu,cid:bv,goto:l,uri:bw,pic:S,pic_4_3:bx,title:by,duration:bz,pubdate:bA,owner:{mid:bB,name:bC,face:bD},stat:{view:bE,like:bF,danmaku:K,vt:a},av_feature:c,is_followed:b,rcmd_reason:{reason_type:b},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:a,bvid:d,cid:a,goto:bG,uri:d,pic:d,pic_4_3:d,title:d,duration:a,pubdate:a,owner:c,stat:c,av_feature:c,is_followed:a,rcmd_reason:c,show_info:a,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:{id:a,contract_id:d,res_id:a,asg_id:a,pos_num:b,name:T,pic:bH,litpic:d,url:U,style:a,is_ad:e,agency:d,label:d,intro:d,creative_type:a,request_id:bI,creative_id:V,src_id:N,area:a,is_ad_loc:e,ad_cb:bJ,title:T,server_type:b,cm_mark:b,stime:a,mid:d,activity_type:a,epid:a,sub_title:d,ad_desc:"AI变现训练营",adver_name:bK,null_frame:f,pic_main_color:d,card_type:a,business_mark:bL,inline:{inline_use_same:a,inline_type:a,inline_url:d,inline_barrage_switch:a},operater:d},is_stock:a,enable_vt:a,vt_display:d,dislike_switch:a,fresh_idx:a},{id:H,bvid:bN,cid:bO,goto:l,uri:bP,pic:x,pic_4_3:x,title:bQ,duration:bR,pubdate:bS,owner:{mid:bT,name:bU,face:bV},stat:{view:bW,like:bX,danmaku:bY,vt:a},av_feature:c,is_followed:a,rcmd_reason:{content:bZ,reason_type:o},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:I,bvid:b_,cid:b$,goto:l,uri:ca,pic:X,pic_4_3:cb,title:cc,duration:cd,pubdate:ce,owner:{mid:cf,name:cg,face:ch},stat:{view:ci,like:cj,danmaku:ck,vt:a},av_feature:c,is_followed:a,rcmd_reason:{reason_type:a},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a},{id:J,bvid:cl,cid:cm,goto:l,uri:cn,pic:Y,pic_4_3:co,title:cp,duration:cq,pubdate:cr,owner:{mid:cs,name:ct,face:cu},stat:{view:cv,like:cw,danmaku:cx,vt:a},av_feature:c,is_followed:a,rcmd_reason:{reason_type:a},show_info:b,track_id:k,pos:a,room_info:c,ogv_info:c,business_info:c,is_stock:a,enable_vt:a,vt_display:d,dislike_switch:b,fresh_idx:a}],side_bar_column:[{id:cy,goto:"ogv",track_id:d,pos:b,card_type:y,card_type_en:cz,cover:"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbangumi\u002Fimage\u002Fdbfefc0da48fc486868485e697c1e0ca0f0fdfdf.png",url:cA,title:cB,sub_title:"终极奇幻头脑战",duration:Z,stats:{follow:z,view:_,danmaku:2897,reply:1272,coin:2427,series_follow:z,series_view:_,likes:25176,favorite:z},room_info:c,new_ep:{id:819780,index_show:cC,cover:"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002Fd8412c0b19135ac9b44aada64bb1e811752491c3.png",title:"6",long_title:"头脑竞技场",pub_time:"2024-05-06 20:30:00",duration:Z,day_of_week:b},styles:["奇幻","智斗","小说改","冒险"],comic:c,producer:[{mid:928123,name:"哔哩哔哩番剧",type:o,is_contribute:b}],source:d,av_feature:c,is_rec:a,is_finish:a,is_started:b,is_play:b,horizontal_cover_16_9:cD,horizontal_cover_16_10:"https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbangumi\u002Fimage\u002F6dfff6143e701de6651e22ae17dd368e355e43a2.png",enable_vt:a,vt_display:d}],business_card:c,floor_info:[{id:A,name:cE,rows:b},{id:a,name:d,rows:b},{id:t,name:y,rows:b},{id:q,name:$,rows:b},{id:cF,name:cG,rows:b},{id:cH,name:cI,rows:b},{id:o,name:cJ,rows:b},{id:u,name:cK,rows:b},{id:cL,name:cM,rows:b}],user_feature:c,preload_expose_pct:L,preload_floor_expose_pct:L,mid:1959817098},recommendInline:{},head:{floorInfo:[{id:-2,sidebar:f,class:g,main:{type:"EvaCardList",head:{icon:"ChannelSpread",name:"推广"},params:{id:34}},rows:b},{id:A,sidebar:f,class:"bili-grid no-margin",main:{type:"BattleArea",head:{icon:"ChannelCompetition",name:cE,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fgame\u002Fmatch\u002F"},params:{id:3449}},rows:b},{id:b,sidebar:e,class:g,main:{type:"LiveCardList",head:{icon:"ChannelLive",name:"直播",link:"https:\u002F\u002Flive.bilibili.com\u002F"}},aside:{type:"LiveRankList"},rows:b},{id:cN,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelDouga",name:"动画",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fdouga"},params:{rid:b}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fdouga"},params:{rid:b}},rows:b},{id:t,sidebar:e,class:g,main:{type:"BangumiArea",head:{icon:"ChannelAnime",name:y,alias:y,link:cO},params:{season_type:b},bottom:{aside:{head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fbangumi",report:{name:y,id:t}},params:{season_type:b}},class:g,main:{head:{id:-20001,name:"番剧动态",link:cO}}}},rows:b},{id:q,sidebar:e,class:g,main:{type:"GuoChuangArea",head:{icon:"ChannelGuochuang",name:$,alias:"国产动画",link:cP},params:{season_type:q},extra:{aside:{head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fguochan",report:{name:$,id:q}},params:{season_type:q}}},bottom:{class:g,main:{type:m,head:{id:-40001,name:"国产原创相关",link:cP},params:{rid:cQ}},aside:{head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fguochuang"},params:{rid:cQ}}}},rows:b},{id:cR,sidebar:e,class:g,main:{type:"VarietyArea",head:{icon:"ChannelZongyi",name:"综艺",link:"https:\u002F\u002Fwww.bilibili.com\u002Fvariety\u002F"}},rows:b},{id:cF,sidebar:e,class:g,main:{type:"MangaCardList",head:{icon:"ChannelManhua",name:cG,link:"https:\u002F\u002Fmanga.bilibili.com\u002F"}},aside:{type:"MangaRankList"},rows:b},{id:cS,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelMusic",name:"音乐",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fmusic"},params:{rid:o}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fmusic"},params:{rid:o}},rows:b},{id:M,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelDance",name:"舞蹈",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fdance"},params:{rid:cT}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fdance"},params:{rid:cT}},rows:b},{id:cU,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelGame",name:"游戏",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fgame"},params:{rid:q}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fgame"},params:{rid:q}},rows:b},{id:12,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelKnowledge",name:"知识",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fknowledge"},params:{rid:cV}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fknowledge"},params:{rid:cV}},rows:b},{id:cH,sidebar:e,class:g,main:{type:"CheeseCardList",head:{icon:"ChannelZhishi",name:cI,link:"https:\u002F\u002Fwww.bilibili.com\u002Fcheese"}},aside:{type:"CheeseRankList",head:{name:i,class:j}},rows:b},{id:13,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelTech",name:"科技",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Ftech"},params:{rid:cW}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Ftech"},params:{rid:cW}},rows:b},{id:14,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelSports",name:"运动",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fsports"},params:{rid:cX}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fsports"},params:{rid:cX}},rows:b},{id:15,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelCar",name:"汽车",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fcar"},params:{rid:cY}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fcar"},params:{rid:cY}},rows:b},{id:P,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelLife",name:"生活",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Flife"},params:{rid:cZ}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Flife"},params:{rid:cZ}},rows:b},{id:17,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelFood",name:"美食",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Ffood"},params:{rid:c_}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Ffood"},params:{rid:c_}},rows:b},{id:18,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelAnimal",name:"动物圈",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fanimal"},params:{rid:c$}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fanimal"},params:{rid:c$}},rows:b},{id:20,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelKichiku",name:"鬼畜",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fkichiku"},params:{rid:da}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fkichiku"},params:{rid:da}},rows:b},{id:22,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelFashion",name:"时尚",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Ffashion"},params:{rid:db}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Ffashion"},params:{rid:db}},rows:b},{id:21,sidebar:e,class:g,main:{type:"InformationArea",head:{icon:"ChannelInformation",name:"资讯",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Finformation"},params:{rid:202}},rows:b},{id:dc,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelEnt",name:"娱乐",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fent"},params:{rid:u}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fent"},params:{rid:u}},rows:b},{id:26,sidebar:e,class:g,main:{type:"ArticleCardList",head:{icon:"ChannelRead",name:"专栏",link:"https:\u002F\u002Fwww.bilibili.com\u002Fread\u002Fhome"}},aside:{type:"ArticleRankList",head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fread\u002Franking#type=3"}},rows:b},{id:o,sidebar:e,class:g,main:{type:aa,head:{icon:"ChannelMovie",name:cJ,link:"https:\u002F\u002Fwww.bilibili.com\u002Fmovie\u002F"},params:{rid:dc}},aside:{type:ab,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fmovie"},params:{season_type:t}},rows:b},{id:u,sidebar:e,class:g,main:{type:aa,head:{icon:"ChannelTeleplay",name:cK,link:"https:\u002F\u002Fwww.bilibili.com\u002Ftv\u002F"},params:{rid:cU}},aside:{type:ab,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Ftv"},params:{season_type:u}},rows:b},{id:25,sidebar:e,class:g,main:{type:m,head:{icon:"ChannelCinephile",name:"影视",link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fcinephile"},params:{rid:dd}},aside:{type:n,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fcinephile"},params:{rid:dd}},rows:b},{id:cL,sidebar:e,class:g,main:{type:aa,head:{icon:"ChannelDocumentary",name:cM,link:"https:\u002F\u002Fwww.bilibili.com\u002Fdocumentary\u002F"},params:{rid:177}},aside:{type:ab,head:{name:i,class:j,link:"https:\u002F\u002Fwww.bilibili.com\u002Fv\u002Fpopular\u002Frank\u002Fdocumentary"},params:{season_type:o}},rows:b}],business:[],banner_card:{},recommend:[{freshIdx:a,goto:l,title:ar,aid:B,cid:ao,bvid:an,cover:O,pic:O,pic_4_3:aq,pubdate:at,enable_vt:a,author:{name:av,mid:au,face:aw},isAd:f,url:ap,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F482867012",stats:{view:ax,like:ay,danmaku:az,vt:a,vt_display:d},duration:as,spmInfo:{spmid:r,mod:s,idx:b},isFollowed:f,rcmdReason:{content:aA,reason_type:o},showInfo:e,track_id:k,dislike_switch:b,key:B,locId:p,freshType:a},{freshIdx:a,goto:l,title:aE,aid:C,cid:aC,bvid:aB,cover:v,pic:v,pic_4_3:v,pubdate:aG,enable_vt:a,author:{name:aI,mid:aH,face:aJ},isAd:f,url:aD,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F3816626",stats:{view:aK,like:aL,danmaku:aM,vt:a,vt_display:d},duration:aF,spmInfo:{spmid:r,mod:s,idx:t},isFollowed:f,rcmdReason:{content:h,reason_type:a},showInfo:e,track_id:k,dislike_switch:b,key:C,locId:p,freshType:a},{freshIdx:a,goto:l,title:aQ,aid:D,cid:aO,bvid:aN,cover:w,pic:w,pic_4_3:w,pubdate:aS,enable_vt:a,author:{name:aU,mid:aT,face:aV},isAd:f,url:aP,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F12188390",stats:{view:aW,like:P,danmaku:a,vt:a,vt_display:d},duration:aR,spmInfo:{spmid:r,mod:s,idx:o},isFollowed:e,rcmdReason:{content:h,reason_type:b},showInfo:e,track_id:k,dislike_switch:b,key:D,locId:p,freshType:a},{freshIdx:a,goto:l,title:a$,aid:E,cid:aY,bvid:aX,cover:Q,pic:Q,pic_4_3:a_,pubdate:bb,enable_vt:a,author:{name:bd,mid:bc,face:be},isAd:f,url:aZ,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F487425891",stats:{view:bf,like:bg,danmaku:bh,vt:a,vt_display:d},duration:ba,spmInfo:{spmid:r,mod:s,idx:q},isFollowed:f,rcmdReason:{content:h,reason_type:a},showInfo:e,track_id:k,dislike_switch:b,key:E,locId:p,freshType:a},{freshIdx:a,goto:l,title:bm,aid:F,cid:bj,bvid:bi,cover:R,pic:R,pic_4_3:bl,pubdate:bo,enable_vt:a,author:{name:bq,mid:bp,face:br},isAd:f,url:bk,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F102438649",stats:{view:bs,like:bt,danmaku:K,vt:a,vt_display:d},duration:bn,spmInfo:{spmid:r,mod:s,idx:u},isFollowed:f,rcmdReason:{content:h,reason_type:a},showInfo:e,track_id:k,dislike_switch:b,key:F,locId:p,freshType:a},{freshIdx:a,goto:l,title:by,aid:G,cid:bv,bvid:bu,cover:S,pic:S,pic_4_3:bx,pubdate:bA,enable_vt:a,author:{name:bC,mid:bB,face:bD},isAd:f,url:bw,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F474380680",stats:{view:bE,like:bF,danmaku:K,vt:a,vt_display:d},duration:bz,spmInfo:{spmid:r,mod:s,idx:cR},isFollowed:e,rcmdReason:{content:h,reason_type:b},showInfo:e,track_id:k,dislike_switch:b,key:G,locId:p,freshType:a},{locId:p,title:T,aid:h,bvid:h,cid:h,cover:bH,author:{name:bK,mid:h,face:h},isAd:e,enable_vt:h,url:U,spaceUrl:U,pubdate:h,stats:{view:h,like:h,coin:h,danmaku:h,vt:h,vt_display:h},duration:h,spmInfo:{mod:"extension",idx:"content",ext:"click"},is_ad_loc:e,creative_id:V,show_url:h,src_id:N,server:h,is_ad:e,operater:d,res_id:a,asg_id:a,area:a,ad_cb:bJ,pos_num:b,mid:d,resource_id:h,server_type:b,id:a,card_type:a,business_mark:bL,request_id:bI,goto:bG,key:V,freshType:a},{freshIdx:a,goto:l,title:bQ,aid:H,cid:bO,bvid:bN,cover:x,pic:x,pic_4_3:x,pubdate:bS,enable_vt:a,author:{name:bU,mid:bT,face:bV},isAd:f,url:bP,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F26385307",stats:{view:bW,like:bX,danmaku:bY,vt:a,vt_display:d},duration:bR,spmInfo:{spmid:r,mod:s,idx:cN},isFollowed:f,rcmdReason:{content:bZ,reason_type:o},showInfo:e,track_id:k,dislike_switch:b,key:H,locId:p,freshType:a},{freshIdx:a,goto:l,title:cc,aid:I,cid:b$,bvid:b_,cover:X,pic:X,pic_4_3:cb,pubdate:ce,enable_vt:a,author:{name:cg,mid:cf,face:ch},isAd:f,url:ca,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F396967836",stats:{view:ci,like:cj,danmaku:ck,vt:a,vt_display:d},duration:cd,spmInfo:{spmid:r,mod:s,idx:cS},isFollowed:f,rcmdReason:{content:h,reason_type:a},showInfo:e,track_id:k,dislike_switch:b,key:I,locId:p,freshType:a},{freshIdx:a,goto:l,title:cp,aid:J,cid:cm,bvid:cl,cover:Y,pic:Y,pic_4_3:co,pubdate:cr,enable_vt:a,author:{name:ct,mid:cs,face:cu},isAd:f,url:cn,spaceUrl:"\u002F\u002Fspace.bilibili.com\u002F486989780",stats:{view:cv,like:cw,danmaku:cx,vt:a,vt_display:d},duration:cq,spmInfo:{spmid:r,mod:s,idx:M},isFollowed:f,rcmdReason:{content:h,reason_type:a},showInfo:e,track_id:k,dislike_switch:b,key:J,locId:p,freshType:a}],aside_card:{goto:cz,ai_params:{pos:b,track_id:d,av_feature:c,source:d,is_rec:a},displayItem:{pic:cD,url:cA,title:cB,isWatched:f,subTitle:cC,id:cy,duration:Z,day_of_week:b,author:{},enable_vt:a,stats:{danmaku:a,view:_,like:z,favorite:z,share:a,vt:a,vt_display:d,online:a,area:d}},freshType:a},ad:[],preload_expose_pct:L,preload_floor_expose_pct:L},dynamicUpList:[],specialRcmdFloor:[],haveFetchSpecialRcmdFloor:f}}}}(0,1,null,"",true,false,"bili-grid",void 0,"排行榜","rank-title","web_pegasus_3.router-web-pegasus-1491226-84f84d7976-njvft.1715073695128.727","av","VideoCardList","VideoRankList",3,5613,4,"333.851","b_7265636f6d6d656e64",2,5,"http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002F0ea6e751ccaa3a5311261f3081922a48874ffe8c.jpg","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002F3419a591aeef4a53ea66e754a2f535e1d0daac85.jpg","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002Fb1f82fd8c2b6692498487c4dbdccc9e8b9a099e2.jpg","番剧",105121,-1,1752410818,1003064936,1703793439,1653327492,1903342555,1053704434,1003850291,1353614413,1353009029,48,.5,10,5614,"http:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Farchive\u002F26d3051cf0e42ecec582c0cc7d71c4ed04be561b.jpg",16,"http:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Farchive\u002Fbf0fe03778c678ba9760aa8b983c66f3c2223668.jpg","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Farchive\u002Fc7192b303df325ee36a63b856ff90d7e83ac7e6d.jpg","http:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Farchive\u002F49bbb6f72877f1336f46b9853bd09b2fd22f5ca3.jpg","别拉不下面子,你真应该抓住风口学AI搞钱","https:\u002F\u002Fht.nextclass.com\u002FCMS\u002Fprod\u002F5264\u002F288\u002Fhome.html?mantisSiteId=7188&track_id=pbaes.Z4e0-VNVpS3ADLCsn_QpkAdkcSOplRvCKp2Mv860iA9bLHYhWOvRXIJzh1Jxt8-NcLUtHNsK_eVvvK1qePEjOfTy4NXcLvcuCocvQuCLX4Y3xVsb2E8WjCuNlGwCwCeOvSnCasX9B4CakM9-fW9MacJcTKHeSv0VPG3oEuZ77COEKB8wAnC-vGrrq-ge3v3i",137712978,"#999999FF","http:\u002F\u002Fi2.hdslb.com\u002Fbfs\u002Farchive\u002Feb6e82f102367f1a197613c0288d77975f0a93e0.jpg","http:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Farchive\u002F5ff1572ae4eac86a217f2d80f8ed2b758649097e.jpg",1421000,2558082,"国创","MovieCardList","PgcRankList","V8",{},{},{},{},{},{},{},{},{},{},"BV1jx421X7zH",1482489574,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1jx421X7zH","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-03-26-1645081752410818_1612_gener.jpg","10分钟速通计算机网络 每个开发者都具备的计算机常识",638,1711442700,482867012,"吴悠讲编程","https:\u002F\u002Fi2.hdslb.com\u002Fbfs\u002Fface\u002Fd5e3033e9e62a76e2706929257797a85264be235.jpg",229545,14819,502,"1万点赞","BV1Vx4y1a7VB",1503968642,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1Vx4y1a7VB","当我来到世界尽头",1100,1713002400,3816626,"Linksphotograph","https:\u002F\u002Fi2.hdslb.com\u002Fbfs\u002Fface\u002F2827281d7fd11cd62d9cc355039860cd2979970b.jpg",2203019,129662,7286,"BV1hT421C7PP",1526653343,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1hT421C7PP","K8S即职场(一)",666,1714552793,12188390,"佚名运维","https:\u002F\u002Fi2.hdslb.com\u002Fbfs\u002Fface\u002Fa3ad52d6ee0d925ea07f4aafe23881a89c43355e.jpg",336,"BV1sE421M77B",1512431456,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1sE421M77B","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-04-19-16492689701653327492_16_12_4614_crop.jpg","突袭100个同事键盘,每个都好想要!!!",800,1713516565,487425891,"可以去你家嘛","https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fface\u002Fb704334fbd140aebaf16cc8d834ed22cc08f6e67.jpg",2796054,24998,3419,"BV17m411U7cC",1513619117,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV17m411U7cC","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-04-20-14431055071903342555_16_12_440_crop.jpg","30分钟Shell光速入门教程",1454,1713595388,102438649,"GeekHour","https:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Fface\u002Fedbf5d5a620567195155dde1e7fe9ef324733cd3.jpg",57251,2644,"BV1cH4y1P7AT",1519567020,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1cH4y1P7AT","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-04-25-17363763151053704434_16_12_3788_crop.jpg","【2024安卓开发】Android转行有哪些最优选择?需要具备哪些技能?",1067,1714037796,474380680,"Android架构解析","https:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Fface\u002F68cd83c7a9f2f39667636a7880f152230566102d.jpg",6650,120,"ad","https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fsycp\u002Fcreative_img\u002F202404\u002Fd1060048b5db15af37fe8f3d673ed0e4.jpg","1715073695143q172a25a155a11q357","CJO1zAIQxfn8DBjSqtVBINUeKAEwl9+PATjuK0IfMTcxNTA3MzY5NTE0M3ExNzJhMjVhMTU1YTExcTM1N0in++6S9TFSBuS4iua1t1oG5LiK5rW3YgbkuK3lm71oA3AAeICAgICQGIABAYgBAJIBDjExNC45Mi4yMjguMjQ4oAGqA6gBNLIBIJl83L6psoBq14zO\u002FIeXaWr31O3FKO7XfeeOJxGQpEv2ugGWAmh0dHBzOi8vaHQubmV4dGNsYXNzLmNvbS9DTVMvcHJvZC81MjY0LzI4OC9ob21lLmh0bWw\u002FbWFudGlzU2l0ZUlkPTcxODgmdHJhY2tfaWQ9cGJhZXMuWjRlMC1WTlZwUzNBRExDc25fUXBrQWRrY1NPcGxSdkNLcDJNdjg2MGlBOWJMSFloV092UlhJSnpoMUp4dDgtTmNMVXRITnNLX2VWdnZLMXFlUEVqT2ZUeTROWGNMdmN1Q29jdlF1Q0xYNFkzeFZzYjJFOFdqQ3VObEd3Q3dDZU92U25DYXNYOUI0Q2FrTTktZlc5TWFjSmNUS0hlU3YwVlBHM29FdVo3N0NPRUtCOHdBbkMtdkdycnEtZ2UzdjNpwgEDMTgy0gEA2AHBAeABgJTr3APoAcCEPfABAPgBiQOAAgKIAgCSAscBMTY5NjI2NjFfMTcxNDUyMDQ2NywyNTg2MTE1NF8xNzE0NTI5ODY4LDI1ODY3MjM0XzE3MTQ1NDg3MzEsMjQ5MDczNDhfMTcxNDYwOTE1NywyNzA2NjM5Nl8xNzE0NzE2ODkyLDIzODA2ODYzXzE3MTQ3MjE2NzQsMjY4NjMzNThfMTcxNDgwMzkyNiwyNjgzNDgwMV8xNzE0ODIyNjg1LDI1MjEwNzQ2XzE3MTQ4OTI0MTksMjc2MzM4NTNfMTcxNDk1MTg5OJgChZKeCKAC3HGoAt6pFbAC5QK4AgDAAoCU69wDyALgAeoCAPgCssUBiAMBkgMAqAMAsAMAuAMAyAMY0gOUAXsiMSI6IjEzNzcxMjk3OCIsIjEyIjoiNTYxNCIsIjEzIjoiMjE5MDA0NSIsIjE0IjoiMjc1IiwiMTUiOiIzMDYiLCIxNiI6IjIxOTAwNDVfMjUyNjYiLCIyIjoiMjM1NTA5NSIsIjMiOiIyMzU1MDk1IiwiNCI6IjM4IiwiNSI6IjMyNyIsIjYiOiIyMzU1MDk1In3gAwLoAwLwAwD6AwVvdGhlcoIECW51bGw6bnVsbIgEqgOQBACgBCKqBAcIyrLPBhAEqgQHCKPVzAYQAbgECsAEBNAEANgEAOIErQE1Ni57ImZvcmNlVHVubmVscyI6eyIxODgxIjo1ODYyfSwicHNJZCI6MTk4MDAsInYyIjoiQ1VrejE1Q1drVGFEVnRsYm1Pa2lDd0dGSWRuWF81QS1FMG82WmN5LVFYdTFxZVVDVTJTN3lQeGMyOUpPQWE2Q1g2bVAyMW5XajgycmEtMjZYRGVSZ3JpUEJnIn07NjMueyJwc0lkIjoxOTcyNCwidjIiOiJBSW8ifegEAPAEAPoE7gJ7ImFjY2VsZXJhdGVfZmFjdG9yIjoxLjAsImFjY2VsZXJhdGVfaWQiOjAsImFkdnZfaW5mbyI6IntcImFkanVzdF9iZWZvcmVfY29zdFwiOlwiMzkzLjE5MFwiLFwiYWRqdXN0X3JhdGlvXCI6XCIxLjkxMFwiLFwiY29zdF9kaWZmXCI6XCIzNTcuOTc1XCJ9IiwiYml6X3R5cGUiOjQsImNwYSI6IntcImNwYV9sZXZlbFwiOjIsXCJjcGFfc2V0XCI6OTUwMH0iLCJleHBsb3JlX3JhdGlvIjoiMTAwIiwibW9kZWxTY29yZSI6IntcImN0clwiOlwiNTIuMjYyNTU0XCIsXCJjdnJfbDBcIjpcIjIyNC43MTk5NTVcIixcImZpbmFsX3BjdHJcIjpcIjUyLjI2MjU1NFwiLFwiZmluYWxfcGN2clwiOlwiMjI0LjcxOTk1NVwifSIsInZpZGVvX3VwX21pZCI6MH2ABQCQBSiQBTOQBUOQBUiQBUmQBXKQBbMBkAW0AZAF0AGQBdEBkAXXAZAF2AGQBYkCkAWOApAFmgKQBakCkAWqApAFwAKQBcICkAXDApAFxQKQBcsCkAXOApAF0wKQBdYCkAXXApAF2AKQBdkCkAXaApAF3wKQBeECkAXjApAF5AKQBeUCkAXmApAF8AKQBfUCkAX7ApAF\u002FwKQBY0DkAWUA5AFlQOQBZgDkAWZA5AFmgOQBZsDkAWgA5AFpQOQBacDkAWwA5AFtgOQBbcDkAXAA5AFwQOQBc0DkAXUA5AF4AOQBeYDkAXzA5AF9QOQBfgDkAX\u002FA5AFtASQBd0EkAXGBZAFjwa4BQTABd3VhQHIBQk=","遍知教育",{},"#686868","BV1ox4y1B7gS",1524240212,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1ox4y1B7gS","结束12年的婚姻后,一些想对你们说的心里话",417,1714383362,26385307,"朱莉姐姐Julie","https:\u002F\u002Fi1.hdslb.com\u002Fbfs\u002Fface\u002Fc6c43c59b9eabf0f7513469258eed6751368dcd7.jpg",1165117,47718,3343,"4万点赞","BV19z42167uq",1520487966,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV19z42167uq","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-04-26-17002650981353614413_16_12_7325_crop.jpg","120秒学会10种旅拍 【大师运镜】",233,1714122000,396967836,"哲瀚去拍摄了","https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fface\u002Fd12e1a55c15445f62f4a07efa7e7511e77d74312.jpg",473925,47750,198,"BV1Fz421C7TZ",1506761971,"https:\u002F\u002Fwww.bilibili.com\u002Fvideo\u002FBV1Fz421C7TZ","http:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Faistory\u002F2024-04-15-19001485291353009029_16_12_9460_crop.jpg","中科院放大招了,偷偷出了4个神器!",70,1713178800,486989780,"老麦的工具库","https:\u002F\u002Fi2.hdslb.com\u002Fbfs\u002Fface\u002F340e09f4bb605a020c6fbefbdd81555b9e70cab6.jpg",1036683,104775,271,47548,"bangumi","https:\u002F\u002Fwww.bilibili.com\u002Fbangumi\u002Fplay\u002Fss47548","神渴望着游戏。","更新至第6话","https:\u002F\u002Fi0.hdslb.com\u002Fbfs\u002Fbangumi\u002Fimage\u002Fe751f1d100577d7b75d48b84abee8379c2745277.png","赛事",28,"漫画",27,"课堂","电影","电视剧",7,"纪录片",8,"https:\u002F\u002Fwww.bilibili.com\u002Fanime\u002F","https:\u002F\u002Fwww.bilibili.com\u002Fguochuang\u002F",168,6,9,129,11,36,188,234,223,160,211,217,119,155,23,181))</script><scripttype="text/javascript"src="//s1.hdslb.com/bfs/cm/cm-sdk/static/js/pc.js"></script><script src="//s1.hdslb.com/bfs/seed/jinkela/short/watchlater-pip/watchlater-pip.umd.js"></script><script nomodule>!function(){var e=document,t=e.createElement("script");if(!("noModule"in t)&&"onbeforeload"in t){var n=!1;e.addEventListener("beforeload",(function(e){if(e.target===t)n=!0;else if(!e.target.hasAttribute("nomodule")||!n)return;e.preventDefault()}),!0),t.type="module",t.src=".",e.head.appendChild(t),t.remove()}}();</script><script nomodule id="vite-legacy-polyfill" src="//s1.hdslb.com/bfs/static/laputa-home/client/assets/polyfills-legacy.5e527900.js"></script><script nomodule id="vite-legacy-entry" data-src="//s1.hdslb.com/bfs/static/laputa-home/client/assets/index-legacy.15022ade.js">System.import(document.getElementById('vite-legacy-entry').getAttribute('data-src'))</script></body>
</html>
5.浏览器对页面进行渲染
浏览器对请求到的静态资源进行渲染
dns 解析
发起 tcp 三次握手
建立 tcp 连接后发起 http 请求
服务器响应 http 请求,返回 html 资源
浏览器解析 html 代码,请求html中的其他静态资源
浏览器渲染页面,呈现画面
目前流行的抓包工具
抓包工具是一种用于网络调试和故障排除的重要工具,它们能够捕获并分析通过网络接口传输的数据包。以下是一些流行的抓包工具:12Wireshark。这是一款免费且开源的网络协议分析工具,支持多种操作系统,包括Windows、Mac、Linux等。它能够捕获TCP/IP协议栈上的所有数据包,并提供实时解析和详细信息。Tcpdump。这款工具专门为Linux系统设计,是一款命令行工具,能够捕获网络数据包并将其输出到终端或文件中。Fiddler。这是一款基于Windows平台的HTTP抓包工具,特别适用于开发人员和测试人员。它可以捕获HTTP/HTTPS请求和响应,并提供多种调试和分析功能。Charles https://www.charlesproxy.com/latest-release/download.do。这是一款跨平台的HTTP抓包工具,支持Windows、Linux和Mac OS X。它同样能够捕获HTTP/HTTPS请求和响应,并提供调试和修改功能。HttpWatch。这是一款基于浏览器的工具,主要用于网站开发和测试。它提供了HTTP请求的详细视图,但不允许用户修改请求或响应。Sniffer Pro。这是一款专业的网络分析工具,适用于Windows平台,能够捕获和分析网络数据包。Snoop。这是Sun Microsystems开发的一款网络分析工具,主要用于分析网络流量和故障排除。这些工具各有特点,适用于不同的场景和需求。例如,Wireshark和Tcpdump适用于更技术性的分析,而Fiddler和Charles则更适合开发人员使用。
谷歌浏览器官网
https://www.google.cn/intl/zh-CN/chrome/POST /log/web?0000171715070715998https%3A%2F%2Fwww.bilibili.com%2F|333.1007.first_level_zone_navigation.more.click||1715070715998|||1311x209|1||{%22b_ut%22:null,%22home_version%22:%22V8%22,%22i-wanna-go-back%22:null,%22in_new_ab%22:true,%22ab_version%22:{%22for_ai_home_version%22:%22V8%22,%22tianma_banner_inline%22:%22CONTROL%22,%22in_theme_version%22:%22CLOSE%22,%22exit_feed_btn%22:%22HIDE%22,%22force_to_feed%22:%22GO%22,%22enable_web_push%22:%22DISABLE%22},%22ab_split_num%22:{%22for_ai_home_version%22:0,%22tianma_banner_inline%22:0,%22in_theme_version%22:1,%22exit_feed_btn%22:53,%22force_to_feed%22:64,%22enable_web_push%22:19}}||A1CD5861-5C58-FDB4-28E8-52CCC76F6B5E80040infoc|zh-CN|null|1 HTTP/2
Host: data.bilibili.com
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:125.0) Gecko/20100101 Firefox/125.0
Accept: */*
Accept-Language: zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2
Accept-Encoding: gzip, deflate, br
Referer: https://www.bilibili.com/
Origin: https://www.bilibili.com
Connection: keep-alive
Cookie: buvid3=5055F8E7-3B72-3F43-6047-9F099DFB771C78257infoc; b_nut=1710826278; _uuid=A1CD5861-5C58-FDB4-28E8-52CCC76F6B5E80040infoc; CURRENT_BLACKGAP=0; CURRENT_FNVAL=4048; buvid_fp=7f92596f05aae748c42535961d629b0d; buvid4=D7FA30A8-46FC-3352-BD14-D30F6376790B79907-024031905-DRw6TCzzDs3nfZjOFWI15g%3D%3D; SESSDATA=3a4b9d52%2C1730620977%2C4c694%2A52CjAPmy3pnPc5hOSE7hLO9w0Mh-PhRy520HI_3jX33Xx8ao6tDKYChjXszYc5dnuHdU4SVkJESXJHQnpRN1BnY25rdUt5aElRcm53cFRfOXM4RUl2bTJCOTY5WEh5WHlTNWV2M2VmeUh0Ujh2YzdxZHZZdFRVdVoyNEV2M1dqV2pMNjZsQlhFODB3IIEC; bili_jct=6f8ba810b1142656b343649d999f7137; DedeUserID=1959817098; DedeUserID__ckMd5=6c778576434db489; rpdid=|(umu)Ym|llk0J'u~ukYRJl|R; enable_web_push=DISABLE; header_theme_version=CLOSE; home_feed_column=4; browser_resolution=1311-209; bp_t_offset_1959817098=928697346751987832; b_lsid=976D51B3_18F522AE3C4
Sec-Fetch-Dest: empty
Sec-Fetch-Mode: no-cors
Sec-Fetch-Site: same-site
Content-Length: 0
TE: trailersHTTP事务
http协议他是客户端发出请求,在服务器正确响应之后,用户看到的结果,这整个过程就是一个http事务
