西部数码网站管理助手使用教程网投网站怎样建
Python中的循环 包括 while循环与for循环,本文以while循环为主。
Python中所有的知识点,都是为了解决某个问题诞生的,就好比中文的汉字,每个汉字都是为了解决某种意思表达而诞生的。
1、什么是循环
现实生活中,也有很多循环的应用场景:
(1)食堂阿姨打菜一般流程:接过顾客的餐盘→询问想吃什么菜品→打菜→递回餐盘,重复以上过程,直到所有顾客的菜都打完了
(2)快递员送快递:查看送件地址→赶往目的地→电话告知收件人→收件人签收→交快递件,重复以上过程,直到所有需要送的快递都处理完了。
(3)公交司机……上车---缴费---坐下---下车。
(4)作业流程……布置作业---写作业---交作业---打分---发作业。
以上场景都有一个共同的特点:有条件地重复地做一件事,每一次做的事情不同但类似。
不同地方,比如打饭,有的人想吃的菜不一样。 比如快递,有的人目的地不一样。比如公交,有人去的地方远,缴费就多,不一样。等等。
程序是为了解决实际问题的,实际问题中存在着重复动作,那么程序中也应该有相应的描述,这就是循环。
有了循环之后,就可以把循环中的每个步骤,当成固定部分,类似一个手机模具模型,是固定的,其他各种东西都进来,都要经历这些,最后完成整体步骤。
2、循环的作用
思考:假如我有个女朋友,有一天我们闹矛盾生气了,女朋友说:道歉,说100遍“老婆大人,我错了”。这个时候程序员会怎么做?
按照之前的掌握技能:
答:100遍print('老婆大人,我错了')
太麻烦了,有没有更好的办法呢?我们难道print输出语句要复制粘贴100次嘛?
答:其实不用这么麻烦,以上输出代码中有很多重复的地方,我们只要重复执行100次相同的代码即可,这就是循环!
循环的作用是什么?
答:让代码高效的重复执行
3、循环的种类
在Python中,循环一共分为两大类:while循环与for循环
思考问题:while循环和for循环如何选择呢?
① 对于循环次数已知的情况,建议使用while循环
② 对于循环次数未知的情况,建议使用for循环
while 英 /waɪl/ conj. 当……的时候;与……同时;而,然而(表示对比);尽管,虽然;直到……为止 adv. 在……的时候
for 英 /fɔː(r); fə(r)/ 为了 对……来说 在……时 -------这些都是对于未来那种,未知的。
三、while循环基本语法及其应用
1、while循环的基本语法
对于循环次数已知的情况,建议使用while循环
因为是知道次数的,所以可以用一个计数器。程序里面,计数器一般都是从0开始的,而不是从1开始。
但是如果真的想要从1开始计数,也没关系。
# ① 定义一个计数器(初始化一个计数器)
i = 0或1
# ② 编写while循环结构条件
while 循环条件(判断 计数器 是否达到了目标位置):
循环体1
循环体2
...
# ③ 在循环内部更新计数器-------------如果不更新,那么一直都是一个数,原地不动。让他们+1,可以在某个时间点,某个数值点,达到预定的地方。
i = i + 1 或 i += 1
总结:------------------可以每次都记着这三点,或者把这三点写出来,确保不遗漏,不会错。
while循环三步走
① 初始化计数器
② 编写循环条件(判断计数器是否达到了目标位置)
③ 在循环内部更新计数器
案例:
使用while循环,循环输出100遍“老婆大人,我错了”
代码
# ① 初始化计数器
i = 0
# ② 编写循环条件(判断计数器是否达到了100)
while i < 100:
print('老婆大人,我错了')
# ③ 在循环体内部更新计数器
i += 1
图示

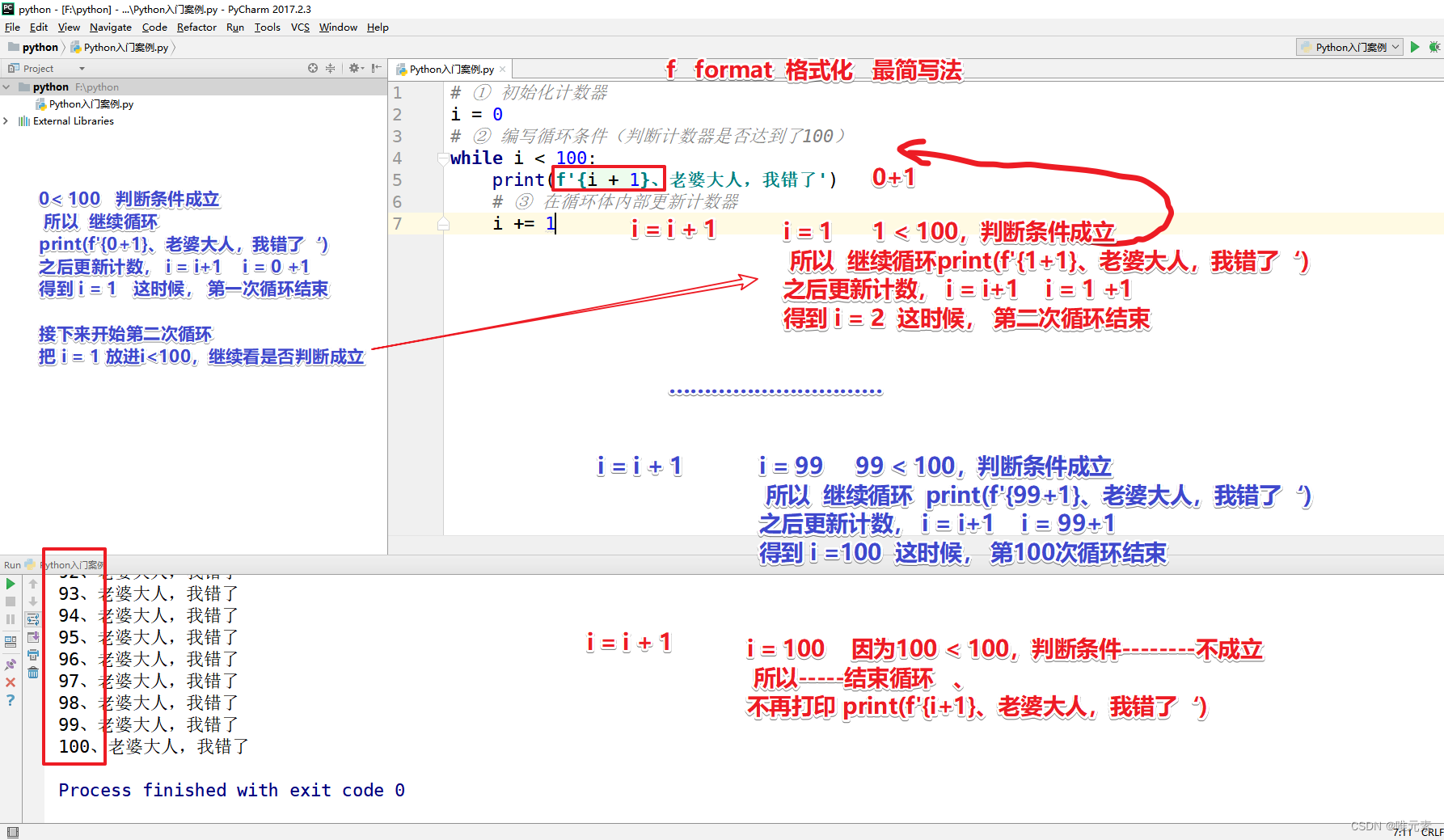
为了看清楚是不是100个----------用f format 格式化 最简写
图示---人话