非法期货做网站学校网站查询个人信息
一、Lambda表达式
-
标准格式

()对应方法的形参 ;->固定格式
-
注意点:
Lambda表达式可以用来简化匿名内部类的书写
Lambda表达式只能简化函数式接口的匿名内部类的写法
函数式接口:
有且仅有一个抽象方法的接口叫做函数式接口,接口上方可以加@Functionallnterface注解
-
Lambda表达式的基本作用
简化函数式接口的匿名内部类的写法
-
Lambda表达式使用前提
必须是接口的匿名内部类,接口中只能有一个抽象方法
-
Lambda的好处
Lambda是一个匿名函数,我们可以把Lambda表达式理解为是一段
可以传递的代码,它可以写出更简洁、更灵活的代码,作为一种更紧
凑的代码风格,使Java语言表达能力得到了提升
-
Lambda表达式的省略写法
省略核心:可推导,可省略
1、参数类型可以省略不写。
2、如果只有一个参数,参数类型可以省略,同时()也可以省略。
3、如果Lambda表达式的方法体只有一行大括号,分号,return可以省略不写,需要同时省略。
二、集合
-
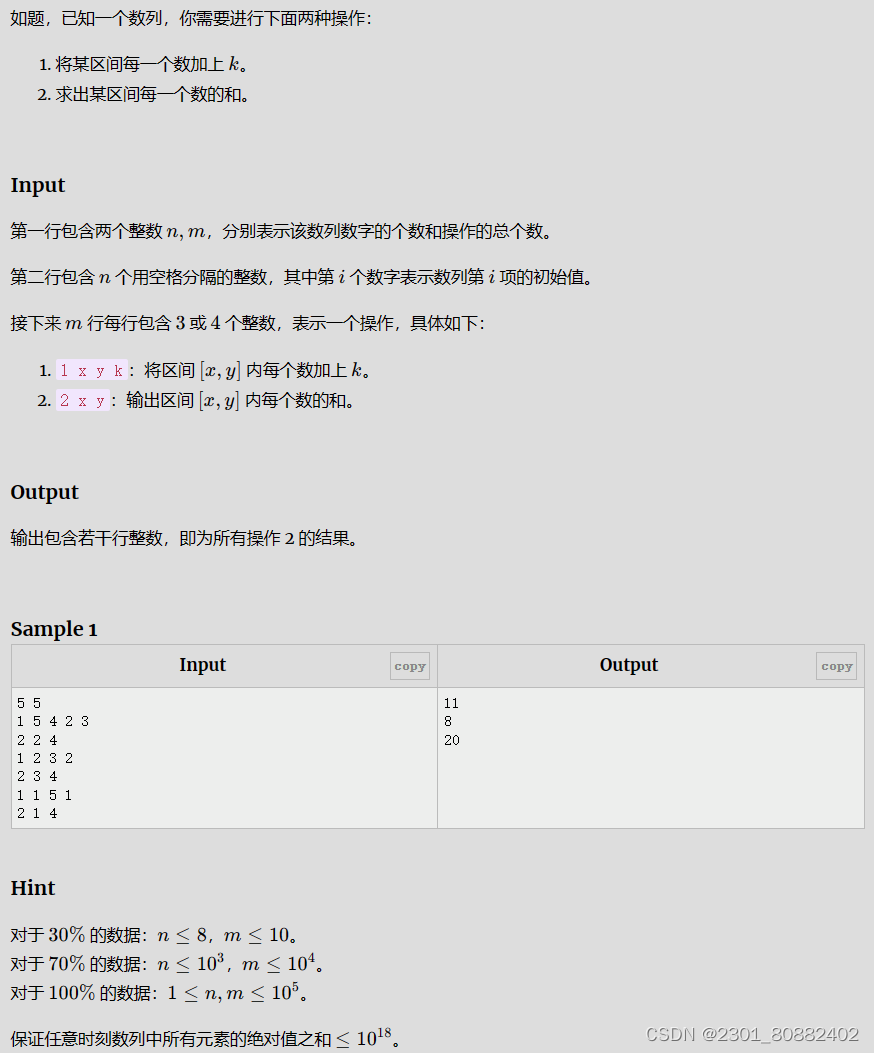
集合体系结构
-
Collection
Collection是单列集合的祖宗接口,它的功能是全部单列集合都可以继承使用的
-
Collection的遍历方式
1、迭代器遍历(迭代器在Java中的类是iterator,迭代器是集合专用的遍历方式)

Collection<String> coll = new ArrayList<>();coll.add("aa");coll.add("bb");coll.add("cc");Iterator<String> it = coll.iterator();while (it.hasNext()){String str = it.next();System.out.println(str);}注意:
- 1、报错NoSuchElementException
- 2、迭代器遍历完毕,指针不会复位
- 3、循环中只能用一次next方法
- 4、迭代器遍历时,不能用集合的方法进行增加或者删除
2、增强for遍历
- 增强for的底层就是迭代器,为了简化迭代器的代码书写的
- 其内部原理就是一个Iterator迭代器
- 所有的单列集合和数组才能用增强for进行遍历

3、Lambda表达式遍历

-
List系列集合:
添加的元素是有序、可重复、有索引
1、特有方法:
- Collection的方法List都继承了
- List集合因为有索引,所以多了很多索引操作的方法

-
Set系列集合:
添加的元素是无序、不重复、无索引
-
五中遍历方式对比

-
ArrayList集合底层原理
1、利用空参创建的集合,在底层创建一个默认长度为0的数组
2、添加第一个元素时,底层会创建一个新的长度为10的数组
3、存满时,会扩容1.5倍
4、 如果一次添加多个元素,1.5倍还放不下,则新创建数组的长度以实际为准
-
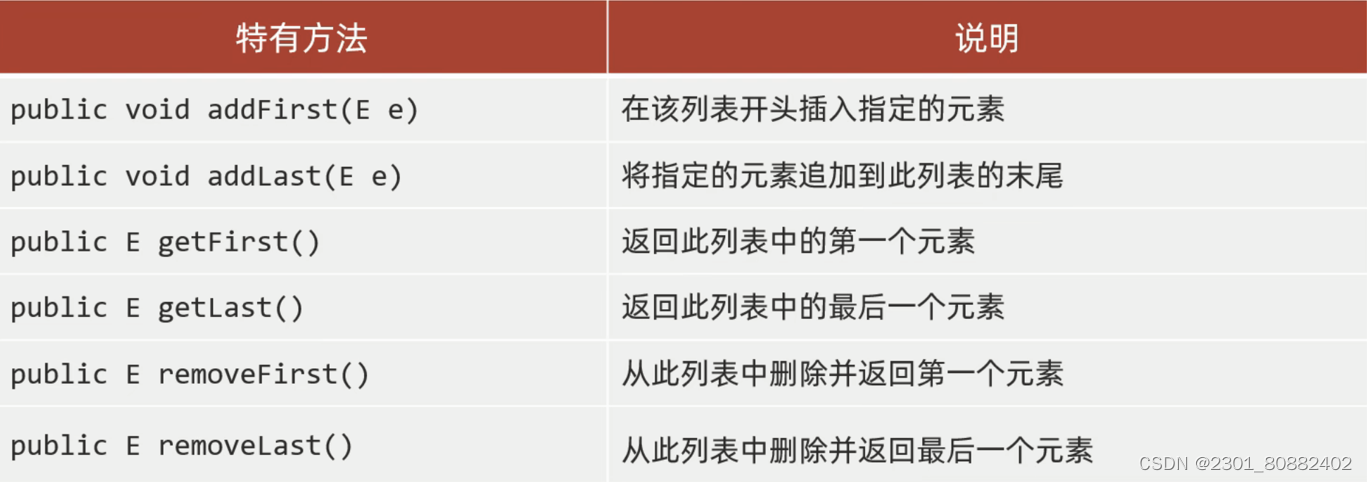
LinkedList集合
- 底层数据结构是双链表,查询慢,增删快,但是如果操作的是首尾元素,速度也是极快的。
- LinkedList本身多了很多直接操作首元素的特有API。
题解:
B - 线段树 1
线段树模版
代码:
#include<stdio.h>
const int N = 1e5+2;
int n, q;
long long s[N], a, b, c;
int f;struct nb
{int l, r;long long lazy;long long sum;
}t[4 * N];void he(int i)
{t[i].sum = t[i * 2].sum + t[i * 2 + 1].sum; //计算每个节点它的子节点的和
}void build(int i, int l, int r) //建立线段树
{t[i].l = l;t[i].r = r;if (l == r){t[i].sum = s[l];t[i].lazy = 0;return;}int mid = (l + r) / 2; //将元素对半分给子节点(不是值,是索引)build(i * 2, l, mid);build(i * 2 + 1, mid + 1, r);he(i);
}void vis(int i) //用于区间修改
{if (t[i].lazy){t[i * 2].sum += t[i].lazy * (t[i * 2].r - t[i * 2].l + 1);t[i * 2 + 1].sum += t[i].lazy * (t[i * 2 + 1].r - t[i * 2 + 1].l + 1);t[i * 2].lazy += t[i].lazy;t[i * 2 + 1].lazy += t[i].lazy;t[i].lazy = 0;}
}long long find(int i, int a, int b) //查找区间和,并返回值
{long long d = 0;if (a <= t[i].l && b >= t[i].r) //如果该节点在该区间内,直接返回该节点的值return t[i].sum;if (t[i].r<a || t[i].l>b) //如果两区间没有交集,直接结束返回0return 0;vis(i);if (t[i * 2].r >= a) //部分在,接着往下搜索d += find(i * 2, a, b);if (t[i * 2 + 1].l <= b)d += find(i * 2 + 1, a, b);return d;
}void add(int i, int a, int b, int c) //修改区间
{if (t[i].l >= a && t[i].r <= b){t[i].sum = t[i].sum + c * (t[i].r - t[i].l + 1);t[i].lazy += c;return;}vis(i);if (t[i * 2].r >= a)add(i * 2, a, b, c);if (t[i * 2 + 1].l <= b)add(i * 2 + 1, a, b, c);he(i);}
int main()
{scanf("%d %d", &n, &q);for (int i = 1; i <= n; i++)scanf("%lld", &s[i]);build(1, 1, n);while (q--){scanf(" %d", &f);if (f == 2){scanf("%lld %lld", &a, &b);printf("%lld\n", find(1, a, b));}else{scanf("%lld %lld %lld", &a, &b, &c);add(1, a, b, c);}}return 0;
}