四川华鸿建设有限公司网站wordpress怎么破解版
大模型对搜推技术产生了深远的影响,极大地推动了搜推技术的演进趋势,使得搜推更加的智能化和个性化,然而在搜推中引入大模型时同样面临一系列的挑战,例如商品知识的幻觉,复杂查询的理解,个性化商品推荐,隐私和安全等问题。
京东零售技术总监翟周伟,基于对电商场景的深刻理解和洞察,从实际问题分析出发,结合京东搜推业务在大模型上的相关创新性实践来解决这些痛点问题,阐述在电商大模型的技术探索。本文为整个演讲的内容文稿,期望对大家有所启发。
作者介绍:翟周伟,京东集团技术总监,负责京东零售搜推电商大模型技术以及在 AI 助手搜推等领域的应用探索和实践。
1. 电商行业的发展和技术演进
1.1 电商行业发展
过去十年,实物商品网上零售额实现了高速增长,电商模式也经历了显著的演变。从以货架电商为主的传统模式,发展到如今货架电商与内容电商并存的多元格局,这一变化不仅反映了市场需求的多样化,也展示了技术进步对零售行业的深远影响。
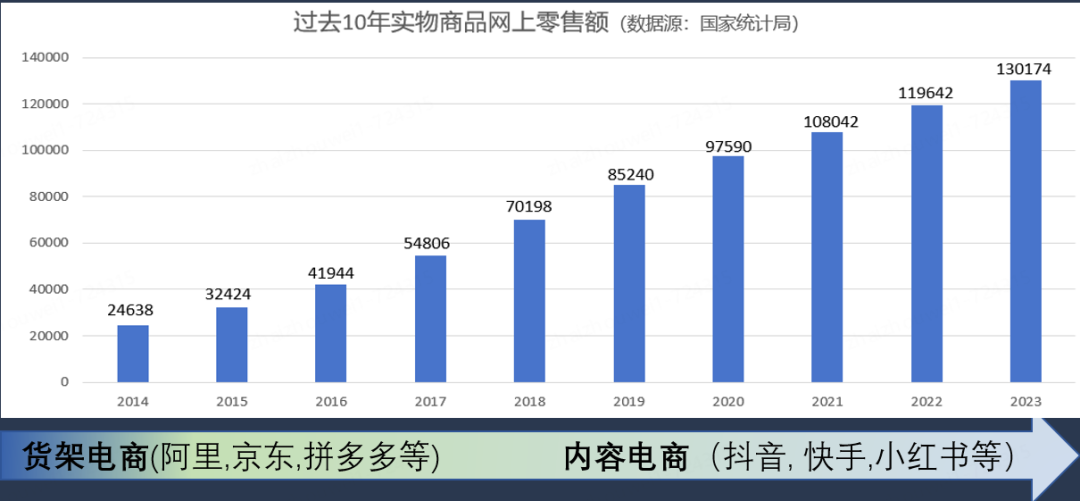
货架电商,如阿里巴巴、京东和拼多多等平台,通过建立庞大的商品数据库和高效的物流体系,为消费者提供了便捷的购物体验。这些平台依托强大的技术基础,优化了供应链管理,降低了商品流通成本,使得消费者能够以更低的价格购买到更丰富的商品。
与此同时,内容电商如抖音、快手和小红书等平台的崛起,标志着电商模式的进一步创新。这些平台通过短视频、直播等内容形式,将商品展示与娱乐体验相结合,吸引了大量用户的关注。内容电商不仅丰富了消费者的购物体验,还通过社交互动和用户生成内容,增强了用户粘性和购买欲望。
本质上,无论是货架电商还是内容电商,都是通过技术驱动,大幅降低了商品流通成本,显著提升了零售效率。可以说,电商模式的发展变化,是技术演进的直接结果。未来,随着技术的不断进步,电商模式将继续创新,进一步满足消费者多样化、个性化的需求。
1.2 电商场景问题分析
从电商用户的消费决策链出发,用户从需求的产生到最终决策下单,可以拆解为购前、购中、购后这三个阶段。在这一链条中,不同类型的平台扮演着不同的角色,各自发挥着独特的功能。
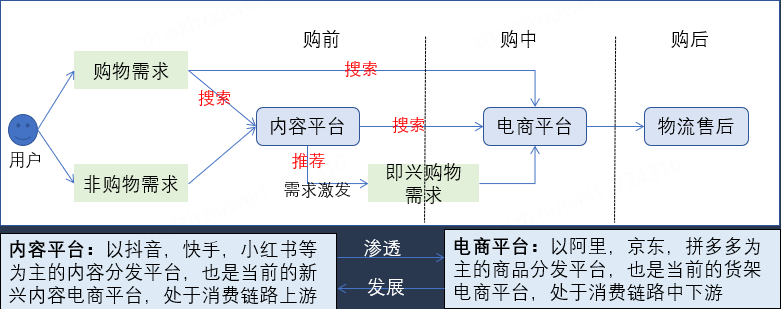
首先,以抖音、快手和小红书等为代表的内容分发平台,作为当前的新兴内容电商平台,主要处于消费链路的上游阶段。在购前阶段,这些平台通过丰富多样的短视频、直播和用户生成内容,激发用户的购物需求。内容电商平台通过生动的商品展示和互动性强的内容,能够有效地吸引用户的注意力,促进潜在需求的产生和转化。用户在这些平台上获取灵感、发现新产品,并逐渐形成购买意向。
而以阿里巴巴、京东和拼多多为代表的商品分发平台,作为当前的货架电商平台,主要处于消费链路的中下游阶段。在购中阶段,这些平台承担着用户需求与商品供给的高效匹配任务。当用户在内容平台上产生购买需求后,他们通常会转向这些电商平台进行搜索,以寻找具体的商品并进行比价和决策。电商平台通过庞大的商品库、精准的推荐算法和高效的物流服务,确保用户能够快速找到所需商品并顺利完成购买。
在消费决策链路中,用户购买需求产生后的搜索环节是决策的关键。电商搜索的核心在于基于用户需求的商品分发,其主要目标是提升商品分发效率,优化的关键指标是 GMV(商品交易总额)和 UCVR(用户转化率)。与一般的信息搜索(如百度)不同,电商搜索不仅要提供相关性高的搜索结果,还需要考虑商品的库存、价格、物流等多方面因素,确保用户能够获得最佳的购物体验。
1.3 关键问题和技术挑战
作为国内领先的电商平台,京东在移动端 APP,小程序以及 PC 端等多种产品形态中,为用户提供了全方位的购物体验。京东的宏观目标是实现更低的成本、更高的效率以及更好的用户体验。然而,在实现这些宏观目标的过程中,京东面临着一系列关键问题和技术挑战。

这种多样化的产品形态要求平台在各个终端上提供一致且优质的用户体验。同时不同终端的用户行为和需求也存在差异,这就需要平台在设计和优化用户界面、功能以及交互体验时,充分考虑各终端的特点和用户习惯。
宏观目标可以总结为:更低的成本、更高的效率和更好的体验。
-
更低的成本:降低成本不仅涉及商品采销和库存管理,还包括物流成本和平台运营成本。通过智能化的供应链管理和 AI 技术,京东可以优化库存配置,减少商品滞销和库存积压,从而降低成本。
-
更高的效率:提高效率主要体现在物流配送和订单处理上。京东通过建设智能物流系统和自动化仓储设施,实现了从订单生成到商品配送的全流程高效运作。同时,通过精准的用户画像和个性化推荐,京东能够在用户浏览和搜索时,更快地匹配到合适的商品,提高用户购物效率。
-
更好的体验:用户体验的提升不仅依赖于界面设计和功能优化,更需要在售前、售中和售后各个环节提供优质的服务。京东通过优化搜索算法、提升客服质量和完善售后服务体系,全面提升用户的购物体验。
在实现宏观目标的过程中,我们需要解决的关键问题可以归结为 GMV(商品交易总额)的问题。GMV 可以通过公式描述为:GMV = UV(独立访客数) * UCVR(用户转化率) * 客单价
-
UV(独立访客数):增加 UV 需要通过多种渠道吸引新用户和保留老用户。京东通过多样化的营销活动、社交媒体推广和内容合作,吸引更多用户访问平台。
-
UCVR(用户转化率):提高 UCVR 需要优化用户的购物路径,减少购买障碍。京东通过改进搜索和推荐系统,提供个性化的商品展示,提升用户的购买意愿。此外,简化支付流程和提供多种支付方式,也有助于提高用户转化率。
-
客单价:提升客单价可以通过增加商品的附加值和鼓励用户购买更多商品来实现。京东通过推出高品质的自有品牌商品和组合销售策略,提升客单价。
在解决上述关键问题时,京东面临着多项技术挑战,这些技术挑战包括但不限于以下四个方面:
-
交互引流
-
提升交互效率同时考虑激发用户需求:在提升用户交互效率的同时,需要设计能够激发用户需求的交互方式。
-
时效性问题:确保信息和商品推荐的实时性,以满足用户的即时需求。
-
丰富性问题:提供多样化的内容和商品选择,满足用户的不同需求。
-
-
意图理解
-
复杂用户需求理解:准确理解用户的复杂需求,提供相应的商品和服务供给。
-
数千数万商品属性和类目精准识别:对海量商品的属性和类目进行精准识别和分类,从而提升检索效率。
-
用户画像等复杂上下文:利用用户画像和上下文信息,提供个性化的商品推荐和服务。
-
-
商品召回
-
多维度召回和融合:从多个维度进行商品召回,确保推荐结果的全面性和准确性。
-
商品和库存等动态变化:实时跟踪商品和库存的动态变化,确保推荐的商品有货且可购买。
-
个性化和多样性问题:在个性化推荐的同时,确保推荐结果的多样性,避免推荐的单一化。
-
-
相关性
-
文本 + 图像多模态匹配:通过文本和图像的多模态匹配,提升推荐结果的相关性。
-
动态价格、促销、物流等:考虑商品的动态价格、促销活动和物流情况,提供更具吸引力的推荐。
-
权衡 UCVR 和长期 GMV:在提升用户转化率的同时,兼顾长期 GMV 的增长。
-
宏观流量调控和反作弊:进行宏观流量调控,防止作弊行为,确保平台的公平性和用户体验。
-
1.4 技术演进洞察
电商行业的快速发展离不开技术的不断创新。技术的演进不仅是为了追求技术本身的突破,更是为了实现更低的成本、更高的效率和更好的用户体验。本节将探讨电商搜索技术的演进历程,从文本检索阶段到当前正在经历的大模型阶段,以及未来的 AGI 导购助手。

文本检索阶段
在电商搜索技术的初期,主要依赖于基础的文本检索技术和规则引擎。这个阶段的核心在于通过关键词匹配实现用户与商品的连接。
-
规则引擎的应用:利用预定义的规则和逻辑,初步实现用户搜索需求与商品信息的匹配。
-
基础文本检索技术:通过简单的文本匹配算法,检索出与用户搜索词相关的商品。
-
关键词的人货匹配:基于关键词的匹配技术,初步实现用户需求与商品的对接。
机器学习阶段
随着数据量的增加和计算能力的提升,电商搜索技术进入了机器学习阶段。这一阶段的核心是通过统计 NLP 和机器学习模型,提升用户意图理解和商品匹配的准确性。
-
用户意图理解和商品理解:通过统计自然语言处理技术,更加精准地理解用户的搜索意图和商品属性。
-
基于 ML 的 CTR/CVR 建模:利用机器学习模型预测点击率(CTR)和转化率(CVR),优化搜索结果的排序。
-
LTR 排序模型:通过学习排序(LTR)模型,进一步提升搜索结果的相关性。
-
用户反馈数据学习:利用用户的搜索和点击反馈数据,不断优化和调整搜索算法,形成基于数据驱动算法迭代闭环。
深度学习阶段
深度学习的兴起,带来了电商搜索技术的又一次飞跃。通过深度神经网络(DNN),电商平台能够更为精准地理解用户意图和商品信息,并实现多模态的搜索交互。
-
基于 DNN 的意图 / 商品精准理解提升分发准确率:利用深度神经网络模型,提升用户意图和商品信息的理解精度,增强泛化效果,从而提高搜索结果的准确性。
-
以文本 + 语音 + 图像的新搜索交互:支持用户通过文本、语音和图像进行搜索,提供更加丰富的交互方式。
-
ANN 语义召回、多模态召回和 DNN 匹配技术:通过近似最近邻(ANN)算法进行语义召回,结合多模态召回和 DNN 匹配技术,提升搜索结果的相关性和多样性。
-
个性化搜索 & 千人千面:根据用户历史行为和偏好,提供个性化的搜索结果,实现千人千面的搜索体验。
大模型阶段
当前电商搜索技术正在经历大模型阶段。基于大模型的技术,不仅提升了用户理解和商品理解的深度和长尾泛化性能,还实现了更加智能的交互方式。
-
交互上单向引导到对话式交互导购:从传统的单向搜索引导,发展到对话式的交互导购,提供更加智能和自然交互的购物体验。
-
基于大模型的用户理解和商品理解解决长尾问题:利用大模型技术,提升对用户需求和商品信息的理解,特别是解决长尾商品的推荐问题。
-
大模型生成式检索技术:在召回和相关性上大模型也正在重构整个技术架构,包括极具有颠覆潜力的大模型生成式检索技术的探索和应用。
AGI 导购助手阶段
展望未来,电商搜索技术将进入 AGI 导购助手阶段。这个阶段的核心是通过完全 AGI 技术驱动,实现多模态交互和 AI Agent 式购物服务。
-
完全 AGI 技术驱动:利用人工通用智能(AGI)技术,全面提升电商搜索和推荐的智能化水平。
-
完全多模态交互:支持文本、语音、图像等多种交互方式,提供更加自然和便捷的购物体验。
-
AI Agent 式购物服务:通过 AI Agent 提供个性化的购物建议和服务,提升用户的购物体验。
-
人格化数字虚拟助理:打造具有人格化特征的数字虚拟助理,为用户提供更加贴心的购物服务。
2. 大模型电商场景下的问题
2.1 大模型的技术优势
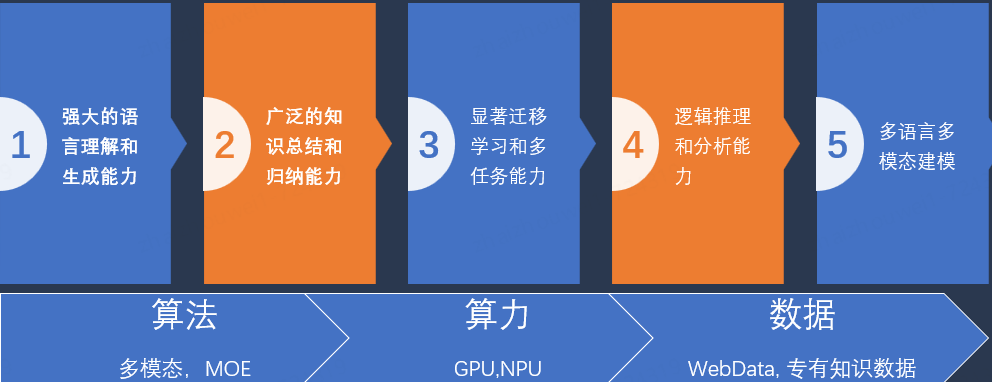
近年来,随着人工智能技术的迅猛发展,大模型在各个领域展现出了卓越的技术优势。大模型不仅在语言理解和生成方面表现出色,还在知识总结、迁移学习、逻辑推理以及多语言多模态建模等方面展现出了强大的能力。以下将详细阐述大模型的五大技术优势。
-
强大的语言理解和生成能力
大模型的一个显著优势在于其强大的语言理解和生成能力。大模型能够准确地理解复杂的语言结构和语义关系,从而实现高质量的文本生成,以及指令遵循能力。这种能力不仅体现在自然语言处理(NLP)任务中,还在搜索和推荐,对话系统和内容创作中得到了广泛应用。
-
广泛的知识总结和归纳能力
大模型具备广泛的知识总结和归纳能力,能够从海量数据中提取和整合信息,形成系统的知识体系。这种能力使得大模型在处理复杂问题时,能够提供全面而准确的解答。
-
显著的迁移学习和多任务能力
大模型在迁移学习和多任务处理方面表现出色。通过迁移学习,大模型可以将从一个任务中学到的知识和技能应用到其他相关任务中,显著提高了模型的泛化能力和适应性。此外,大模型可以基于一个统一模型底座实现多任务学习,这种能力在实际应用中具有重要意义。
-
逻辑推理和分析能力
大模型不仅在数据处理和语言生成方面表现出色,还具备一定的逻辑推理和分析能力。通过复杂的模型结构和训练算法,大模型能够对输入信息进行深度分析和推理,得出合理的结论。这种能力使得大模型在解决复杂问题和做出决策时,能够提供有力的支持。
-
多语言多模态建模
大模型的多语言多模态建模能力,使其在处理多语言和多模态数据时表现出色。大模型可以同时处理文本、语音、图像等多种数据形式,实现跨模态的信息整合和理解。此外,大模型还支持多语言处理,能够在不同语言之间进行无缝转换和理解。这种能力在全球化的背景下具有重要意义。
2.2 电商场景下的应用问题
随着大模型技术的不断进步,其在电商行业的应用也日益广泛。然而,尽管大模型在许多方面展现了强大的潜力,电商场景下的实际应用仍面临诸多挑战。本节将深入探讨电商场景下大模型应用的五大主要问题:电商知识理解、效果和个性化、时效性、成本和速度以及安全性。

电商知识理解
在电商场景中,商品知识的专业性和精确度至关重要。然而,通用大模型在这方面表现出了一些不足。
-
商品知识专业性不足:通用大模型在商品类目、品牌和属性等方面的专业性不够,难以满足电商平台对商品信息的精细化需求。这导致模型在处理商品相关任务时,可能无法提供准确和有用的结果。
-
通用知识和商品的对齐问题:大模型通常基于广泛的通用知识进行训练,但这些知识与具体的商品信息之间存在对齐问题。例如,模型可能无法正确理解某些商品的特定属性或品牌特征。
-
图像商品理解差:尽管大模型在文本处理方面表现优异,但在商品图像商品理解上仍存在显著差距。这限制了其在需要图像识别和处理的电商应用中的效果。
效果和个性化
在电商平台上,个性化推荐和精准营销是提升用户体验和促进销售的关键。然而直接应用大模型并未展现出绝对的效果优势。
-
理解购物历史和偏好:大模型在理解用户的购物历史、偏好、评论和商品细节方面面临挑战。个性化推荐需要对用户统计行为进行深度分析,而通用大模型在这方面的能力有限。
-
个性化挑战:尽管大模型可以处理大量数据,但要实现真正的个性化推荐,仍需克服许多技术难题。例如,如何在短时间内分析和理解用户的复杂需求,并提供精准的商品推荐。
时效性
电商行业的动态性和时效性要求极高,而大模型在这方面存在明显的不足。
-
更新速度慢:大模型本身的更新速度较慢,导致其知识容易陈旧,无法及时反映最新的商品信息、促销活动和价格变动。
-
高时效性需求:电商平台需要实时更新新商品、促销信息和价格变动,以确保用户获取最新的商品信息。然而,大模型在这方面的更新时效性难以满足电商平台的需求。
成本和速度
大模型的训练和推理成本高昂,给电商平台带来了巨大的经济压力。
-
高训练和推理成本:大模型的训练需要大量的计算资源和时间,推理过程也消耗大量的计算能力。这使得其在大规模商用中的 ROI(投资回报率)较低,难以广泛应用。
-
实时性挑战:在线推理速度难以满足电商平台的实时性要求,尤其是在高并发的购物场景中,模型的响应速度成为瓶颈。
安全性
在电商场景中,用户数据的安全性和生成内容的合规性至关重要。
-
用户敏感数据泄露风险:大模型在处理用户数据时,存在敏感数据泄露的风险。这对用户隐私保护和数据安全提出了严峻挑战。
-
生成内容的安全合规:大模型生成的商品相关内容需要确保安全和合规,避免出现虚假信息或不当内容。这对电商平台的内容审核和监管提出了更高要求。
2.3 电商大模型解决方案
基于上述问题分析和大模型优劣势,结合我们京东的业务场景我们提出了一整套基于大模型的 AIGC 架构:
后面章节讲分别介绍整个 AIGC 框架的关键技术

3. 电商大模型关键技术
3.1 数据和预训练
在大模型的预训练过程中,数据预处理是至关重要的一环。特别是在电商领域,数据源的多样性和复杂性决定了预处理的质量直接影响到模型的最终效果。
数据预处理
核心去除站外和站内商品相关数据中的噪音,提升专有数据的电商知识密度,整体流程如下图:
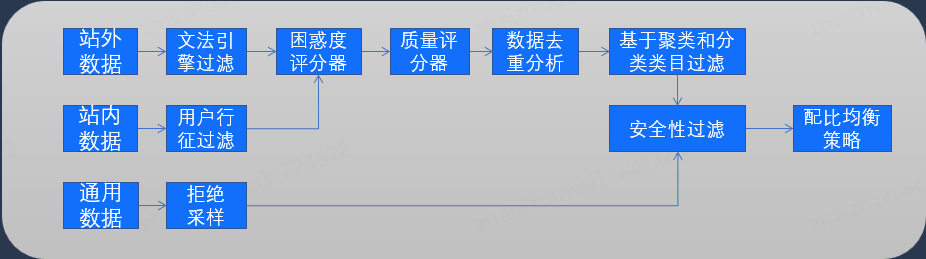
预训练数据处理的核心目标是提升电商知识密度,为了提升大模型在电商领域的专业性和准确性,预处理的核心目标是去除数据中的噪音,确保数据的高质量和高相关性。这不仅有助于模型更好地理解商品类目、品牌和属性,还能提高模型在实际应用中的表现。
数据预处理的核心流程包括以下几个步骤:
-
文法引擎过滤:文法引擎通过分析文本的语法和结构,过滤掉不符合语法规则的噪音数据。这一步骤确保了输入数据的基本语法正确性,减少了模型处理无效信息的负担。
-
困惑度评分器:困惑度评分器用于评估文本的复杂度和合理性。通过计算文本的困惑度,可以识别和过滤掉那些难以理解或不符合常识的内容,从而提高数据的质量。
-
质量评分器:质量评分器根据预定义的标准(如信息完整性、准确性和相关性)对数据进行评分。在技术上一般组合使用多种分类器,可基于 CNN 或 Bert 模型进行构建,只有那些高质量的数据才会被保留下来用于训练模型。
-
数据去重分析:数据去重分析通过识别和删除重复数据,确保训练数据的独特性和多样性,可以使用多种去重算法,这不仅提高了数据的有效利用率,还避免了模型因重复信息而产生的偏差。
-
基于聚类和分类的过滤:通过聚类和分类算法,可以将数据按照不同的类别和特征进行分组和筛选。此步骤有助于识别和过滤掉不相关或低质量的数据,进一步提升数据的电商知识密度。
-
安全性过滤:安全性过滤确保数据不包含敏感信息或违反隐私和安全规定的内容。这一步骤至关重要,特别是在处理用户数据时,必须严格遵守相关的法律法规和隐私政策。
-
数据配比均衡策略:数据配比均衡策略通过调整电商知识类数据和通用数据的比例,确保训练数据的均衡性和全面性。这有助于模型在电商知识增强上充分训练,同时降低对通用能力的损失。
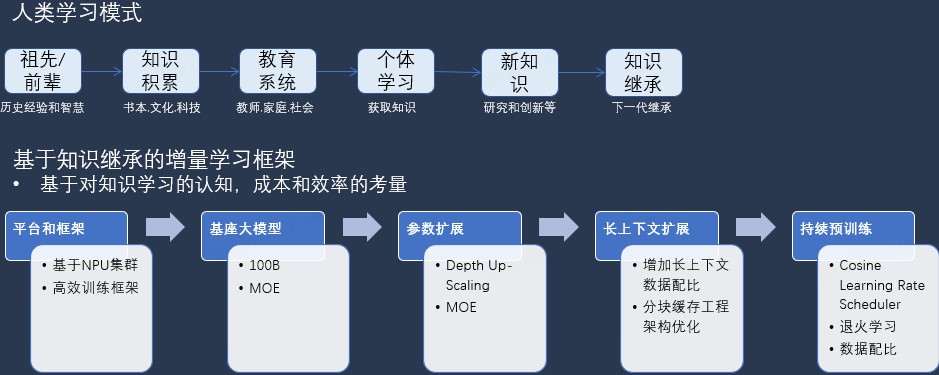
Continue Pretraining: 启发于人类学习总是在前人积累的知识和经验上进一步学习,我们提出了一种基于知识继承的增量学习方法来持续学习,在数据上通过提升电商领域知识密度和配比调整,通过模型结构优化,退火学习,多阶段指令对齐优化,增强安全治理对齐等方法提升我们电商大模型的性能表现。
-
平台和框架
我们的增量学习框架支持基于华为 NPU 集群,利用其强大的计算能力和并行处理优势,实现高效训练。
-
底座大模型
采用支持 100B 参数规模的底座大模型,并结合 MOE(Mixture of Experts)架构,进一步提升模型的表达能力和计算效率。MOE 架构通过动态选择专家网络,显著提高了模型的参数利用率和推理效率,使其在处理复杂任务时表现更加出色。
-
参数扩展
为进一步提升模型的性能和适应性,我们引入了 Depth Up-Scaling 和 MOE 的参数扩展技术。Depth Up-Scaling 通过增加模型的深度,增强其对复杂模式的捕捉能力;MOE 扩展则通过增加专家网络的数量和多样性,提高模型的泛化能力和鲁棒性。
-
长上下文扩展
在处理电商相关长上下文数据时,我们通过增加长上下文数据的配比,并优化分块缓存工程架构,显著提升了模型在长序列任务中的表现。
-
持续预训练
为了实现持续预训练,我们采用了 Cosine Learning Rate Scheduler 和退火学习策略,并结合数据配比调整,确保模型在训练过程中能够逐步适应新的数据和任务。退火学习则通过逐步降低学习率,避免模型陷入局部最优解,提升模型的整体性能。
3.2 通用对齐和领域对齐
对齐学习不仅可以提升模型在通用任务中的表现,还能够在特定领域(如电商)中增强其专业性和准确性。通用对齐学习旨在优化模型对通用指令的遵循能力,使其在广泛的任务中表现出色。同时,电商领域对齐学习则专注于增强模型在电商场景中的专业性。
-
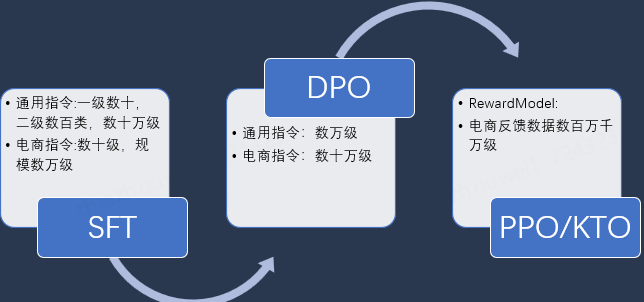
SFT 阶段
在 SFT 阶段,模型通过监督学习进行微调。对于通用对齐,训练数据涵盖各种通用任务和指令,确保模型具备广泛的应用能力。对于电商领域对齐,训练数据则包括大量电商相关的任务和指令,核心是数据多样性和准确率。为了提升多样性和准确性,我们通过对数据进行细粒度的分类标签,并利用更大模型对 SFT 数据在复杂度,准确性等进一步判断筛选判断,最终获取更高指令的对齐数据。
-
DPO 阶段
在 DPO 阶段,模型通过直接偏好优化进行进一步调整。此阶段的目标是提升模型在特定任务中的表现,基于用户反馈或专家的直接反馈进行优化。对于通用对齐,DPO 阶段通过收集用户对模型输出的偏好反馈,调整模型参数,使其更符合用户期望。对于电商领域对齐,DPO 阶段则通过分析用户在电商平台上的行为和反馈作为偏好依据,优化模型在商品推荐和客户服务等方面的表现。
-
PPO 阶段
PPO 阶段采用近端策略优化方法,通过强化学习进一步提升模型的对齐能力。此阶段通过模拟真实环境中的任务和指令执行过程,模型在不断试错和优化中学习最佳策略。对于通用对齐,PPO 阶段使模型能够在动态和复杂的环境中表现出色,具备更强的适应能力。对于电商领域对齐,PPO 阶段则通过电商场景中的各种任务中用户行为反馈使模型能够在搜推应用中考虑搜推的 CTR/CVR 等收益。
在实践中,也可以利用 KTO 对齐来替代 DPO/PPO。
3.3 安全性
随着大模型在各类应用中的广泛部署,其安全性问题日益受到关注。大模型安全性可以从潜在安全事件发生前后进行划分,分别为被动安全和主动安全。这两种策略共同构建了一个全面的安全防护体系,确保大模型的生成内容在各个方面都是安全和可控的,我们设计了一套完整的大模型安全体系:
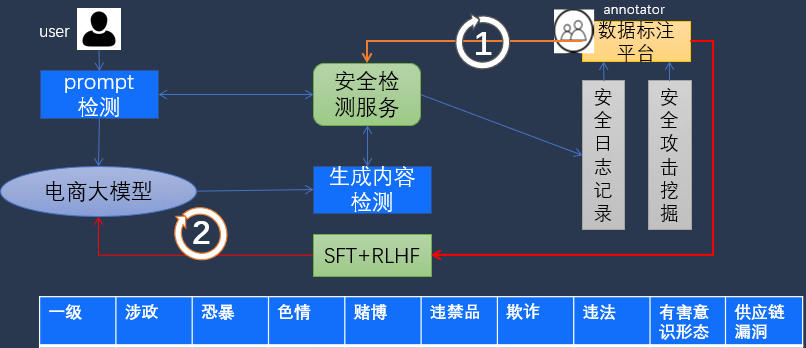
被动安全:安全检测服务
被动安全侧重于安全检测服务,从检测方向入手,确保用户输入的提示词(prompt)和大模型生成的内容在发布前经过严格的安全审查。具体措施包括:
-
用户输入检测:对用户输入的提示词进行实时监控和分析,识别并过滤潜在的恶意或不当内容,防止其对大模型的生成过程产生不良影响。
-
生成内容检测:对大模型生成的内容进行全面的安全审查,检测其中可能存在的幻觉(hallucinations)、毒性(toxicity)、偏见(bias)等问题,确保输出内容符合安全和道德标准。
通过这些检测服务,可以在潜在安全事件发生前及时发现和处理问题,降低风险。
主动安全:大模型生成安全性
主动安全则从生成方向着手,确保大模型在任何输入情况下都能生成安全可控的回复内容。主要技术手段包括监督微调(SFT)和基于人类反馈的强化学习(RLHF)。
-
监督微调(SFT):通过在大量标注数据上进行微调训练,使大模型学习如何生成符合安全标准的内容。训练数据涵盖各种可能的输入场景和生成要求,确保模型具备广泛的安全生成能力。
-
基于人类反馈的强化学习(RLHF):通过收集和分析人类对大模型生成内容的反馈,不断优化模型的生成策略。RLHF 方法能够动态调整模型参数,使其在生成过程中更加注重安全性,减少幻觉、毒性和偏见等问题的出现。
主动安全策略不仅在大模型生成内容的过程中进行实时控制,还通过持续学习和优化,不断提升模型的安全性和可靠性。
被动安全的方法核心是检测,主要方法包括:
-
文法规则引擎: 以句法分析模板 + 词典进行识别,侧重关键词特征明显的文本识别
-
分类模型:以 NN 为核心的小模型,例如基于 bert 的分类,保证一定泛化,同时满足实时要求
-
大模型安全检测:通过 SFT 等技术通过大模型来检测,为了满足低时延往往小参数 LLM 实现
主动安全算法核心是两种思路
-
融合路线:通用对齐 + 电商对齐 + 安全对齐在 SFT 和 DPO 阶段数据融合,PPO 阶段 RewardModel 模型融合
-
两阶段对齐:最后单独进行二阶段的安全对齐
3.4 评估体系
电商大模型的评估体系至关重要。为了确保模型在实际应用中的高效性和可靠性,我们构建了一套综合性的电商大模型评估体系。该体系涵盖了通用 Benchmark、电商 Benchmark 以及安全性评分等多个维度,力求全面、客观地评估模型性能。

通用 Benchmark 评估
通用 Benchmark 评估是衡量大模型在各种标准任务上的表现。我们采用了一系列主流 Benchmark,包括以下但不局限:
-
MMLU:评估模型在多任务语言理解上的能力。
-
CMMLU:针对中文多任务语言理解的评估。
-
C-Eval:评估模型在中文环境下的综合表现。
-
GSM8K:用于评估模型在数学推理任务上的能力。
-
GAOKAO:模拟中国高考题目,评估模型的知识水平和解题能力。
-
SuperCLUE:中文语言理解评估基准。
-
AlignBench:评估模型在对齐任务上的表现。
这些 Benchmark 涵盖了从语言理解到数学推理的多种任务,确保模型在广泛应用中的通用性和鲁棒性。
电商 Benchmark 评估
为了更好地服务于电商应用,我们专门构建了电商 Benchmark。该 Benchmark 与电商应用任务高度对齐,评估模型在电商场景中的具体各种任务表现。评估方法包括自动评估和人工评估:
-
自动评估:利用自动化工具和算法,快速评估模型在电商任务中的表现,裁判模型我们使用 GPT4 作为参考。
-
人工评估:由专业评估人员对模型生成的内容进行人工审核,确保评估结果的准确性和可靠性。
通过电商 Benchmark,我们可以深入了解模型在电商领域的实际应用效果,并进行针对性优化。
安全性评估
安全性是大模型评估中的重要一环。我们通过以下评估集合和指标进行安全性评分:
-
CValues:评估模型输出内容的安全性和合规性。
-
Safety-Prompts:使用特定的安全提示词,测试模型在处理敏感话题时的表现。
-
自建安全评估集:基于实际应用场景,构建专门的安全评估数据集。
安全性 score 计算公式为:Score = 安全回复数量 / 总回复数量或总 prompt 数量
此外,我们还关注错误拒答率(FRR),即大模型误判良性提问场合的概率。
4. 电商搜索场景下大模型应用实践
在电商搜索场景中,大模型能够显著提升用户体验和搜索效率。以下将介绍大模型在电商搜索中的实践应用。
4.1 搜索交互
在电商平台上,搜索交互是用户找到满意商品的关键环节。通过大模型的应用,我们可以实现更智能的 query 引导,帮助用户更快地找到所需商品,同时降低交互成本,提升搜索效率。
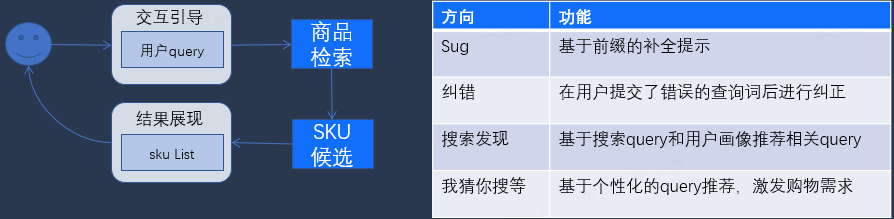
大模型在以下几个方面发挥了重要作用:
-
Query 引导:通过智能引导,帮助用户优化搜索词,提高搜索结果的相关性和满意度。
-
交互成本降低:减少用户在搜索过程中的操作步骤,提高搜索效率。
-
转化率提升:通过精准的搜索结果引流,提升用户的购买转化率。
难点和挑战
尽管大模型在搜索交互中具有显著优势,但也面临一些难点和挑战:
-
传统方法局限:传统的搜索方法主要依赖于召回和排序,利用 SMT(统计机器翻译)和 NMT(神经机器翻译)技术,优化链路较长且噪音大。
-
语言理解挑战:处理歧义、多义词和个性化需求是搜索交互中的主要难点,传统方法难以全面解决这些问题。
-
准确性和泛化效果:在保证搜索结果准确性的同时,提升模型的泛化效果仍然是一个难题。
这里以以纠错 /Sug 等为例说明基于大模型的通用方案:
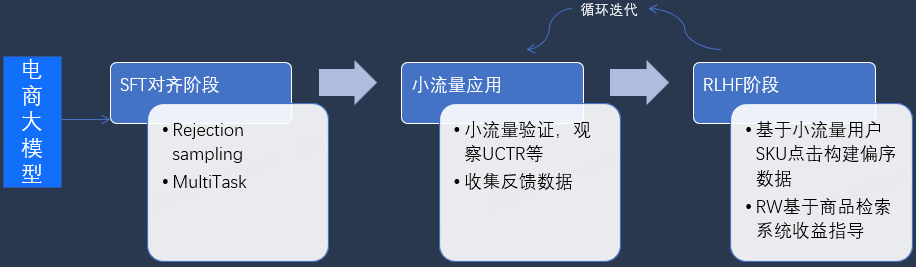
应用核心在于:
-
电商知识增强:将电商领域的专业知识融入大模型中,使其能够更准确地理解和处理用户的搜索需求。
-
业务任务对齐:结合具体的业务任务,对大模型进行优化,使其在搜索交互中表现更佳。
-
搜索交互日志利用:利用历史搜索交互日志,优化模型的对齐目标,提升搜索效果。
-
Multi-Instruction Learning:通过多指令学习,增强模型应对多样化搜索需求的能力。
4.2 电商用户意图理解
在电商平台中,意图理解是提升用户体验和转化率的关键环节。通过解决用户需求表达与商品语义对齐的问题,我们能够提高商品召回的相关性和多样性,最终提升用户转化率(UCVR)。本节将探讨电商意图理解的目标、方向以及面临的问题和挑战,并介绍基于电商大模型的核心技术解决方案。
电商意图理解的主要目标是:
-
解决用户需求表达与商品语义对齐问题:确保用户输入的搜索 query 能够准确匹配到相关商品。
-
提升商品召回的相关性和多样性:提供高相关搜索结果的同时保证结果的多样性,满足不同用户的需求。
-
提升用户转化率(UCVR):通过优化搜索体验和结果,提高用户的购买转化率。

意图理解的方向
为了实现上述目标,意图理解需要在以下几个方向上进行优化:
-
Query 理解:
-
分词:将用户输入的搜索词进行合理的分词处理,提升理解精度。
-
实体识别:识别搜索 query 中的关键实体,如品牌、型号等。
-
类目预测:预测用户搜索的商品类别,提升召回精度。
-
品牌识别:识别并理解用户搜索中的品牌信息。
-
改写:对用户输入的 query 进行智能改写,优化搜索结果。
-
需求识别:理解用户的具体需求,如购买意图、用途等。
-
-
商品理解:
-
商品 SKU 理解:深入理解商品的 SKU 信息,提升匹配度。
-
商品图像理解:通过多模态大模型图像识别技术,理解商品图片内容。
-
SKU-to-Query:实现商品 SKU 信息与用户搜索 query 的精准匹配。
-
问题和挑战
在意图理解的过程中,面临以下主要问题和挑战:
Query 理解:
-
传统方法局限:传统方法主要依赖于规则和基于 BERT 的二分类或多分类、序列标注算法,优化成本高且难以处理长尾问题。
-
长尾问题:用户输入的多样化和个性化需求难以全面覆盖。
商品理解:
-
泛化能力差:商品理解的泛化能力较弱,难以适应多变的商品信息。
-
图像理解准确率低:基于 OCR 的商品图像理解准确率不高,影响搜索结果的精度。
基于电商大模型的意图理解核心技术
为了应对上述问题和挑战,基于电商大模型的意图理解技术应运而生:

我们的大模型应用方案是一个多层体系架构,包括:底层平台层 NPU 平台和 GPU 平台,NPU 是一华为昇腾 910B 为主的第二算力平台,GPU 以 A100/H800 为主;模型底座包括文本大模型和多模态大模型;基于大模型底座我们做了模型扩展和电商知识增强预训练,再通过多任务增强对齐学习构建了我们的电商大模型,最上层是应用层,包括 prompt 工程,进一步结合具体业务场景的对齐以及蒸馏萃取技术,在时效性个性化方便核心是通过 RAG 技术实现的,包括电商知识图谱 RAG,Web 搜索 RAG,以及用户画像 RAG
其核心技术包括:
-
Instruction Learning:通过指令对齐学习,提升模型对多样化需求的理解和处理能力。
-
搜索用户反馈用于强化学习:利用用户搜索行为和反馈数据,对模型进行强化学习,持续优化搜索效果。
-
RAG(Retrieval-Augmented Generation):
-
知识图谱 -RAG:结合知识图谱,增强模型对商品信息的理解和匹配能力。
-
用户画像 -RAG:利用用户画像,提升个性化推荐和搜索结果的精准度。
-
Web 搜索 RAG: 基于公网搜索信息,解决时效性相关知识问题。
-
4.3 文案创意生成
在电商平台中,文案创意是吸引用户关注、提升商品曝光率和转化率的关键因素。然而,传统的文案生成过程往往需要大量的人力和时间成本。随着人工智能技术的进步,利用大模型的生成能力,可以有效降低商品素材的生成成本,提升营销转化效率。本节将探讨电商文案创意生成的具体应用场景和关键技术。
文案创意生成的应用场景
-
商品标题生成:
-
SKU 描述 -> 标题:通过分析 SKU 描述信息,自动生成简洁明了、富有吸引力的商品标题。
-
SKU 描述 + SKU 图像 -> 标题:结合 SKU 描述和商品图像,生成更加精准和视觉化的商品标题。
-
-
商品文案生成:
-
SKU 描述 + 场景 -> 营销文案:基于 SKU 描述和特定使用场景,生成富有创意和吸引力的营销文案,帮助商品更好地触达目标用户。
-
SKU 描述 + SKU 图像 -> 图文文案:结合 SKU 描述和商品图像,生成图文并茂的商品文案,提升用户的阅读体验和购买欲望。
-
-
卖点生成:
-
SKU 商详 -> 卖点:从商品详情中提取核心卖点,帮助用户快速了解商品的主要优势。
-
SKU 商详 + 卖点 -> 卖点文案:结合商品详情和提炼的卖点,生成详细的卖点文案,进一步增强商品的吸引力。
-
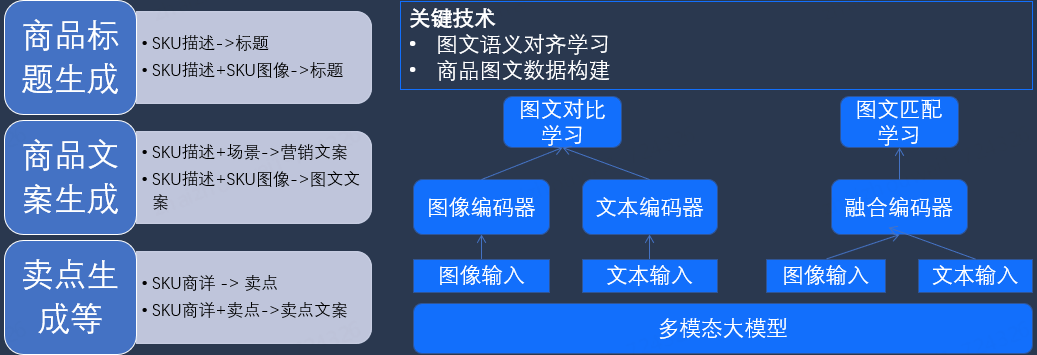
关键技术
为了实现高效且高质量的文案创意生成,以下关键技术至关重要:
-
图文语义对齐学习:通过先进的图文语义对齐技术,确保商品图像与文字描述之间的高度一致性,提升生成文案的准确性和相关性。
-
商品图文数据构建:构建高质量的商品图文数据集,作为训练多模态大模型的基础。通过大量真实商品数据的训练,使模型能够更好地理解和生成符合实际需求的文案。
4.4 电商搜索相关性
在电商平台中,搜索相关性是影响用户体验和购买转化率的关键因素。如何精准匹配用户需求与商品信息,直接关系到用户的搜索满意度和最终的购买决策。本节将探讨电商搜索相关性的核心问题、主流模型以及面临的技术挑战。
核心问题: 电商搜索的核心问题在于如何实现用户需求与商品的精准匹配。这一问题最终可以归结为计算用户搜索 query 与商品 SKU 之间的相关性,即 sim(query, sku)。在优化过程中,不仅要考虑搜索结果的相关性,还需要兼顾点击率(CRT)和转化率(CVR)等关键指标,以实现整体效益的最大化。
主流模型: 目前,基于神经网络(NN)的语义相关性模型在电商搜索中得到了广泛应用,主要分为两大类:
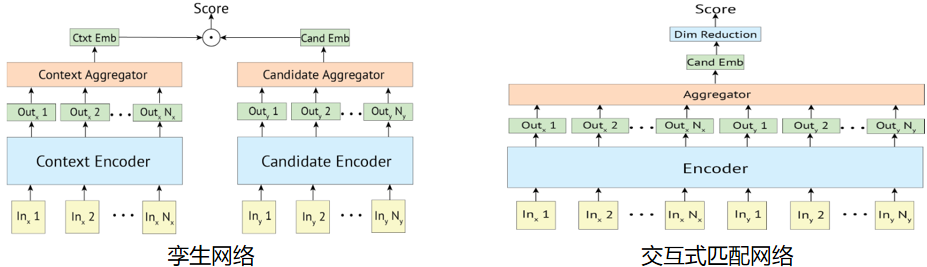
-
孪生网络(Siamese Network):也称双塔模型,孪生网络通过两个或多个共享参数的子网络来处理输入的 query 和 SKU。每个子网络独立地将输入映射到一个高维向量空间,然后计算这两个向量的相似度。这种方法的优点在于计算效率高,适用于大规模的在线搜索场景。
-
交互式匹配(Interactive Matching):也称单塔模型,交互式匹配模型在处理 query 和 SKU 时,允许输入之间进行复杂的交互操作。这种模型能够捕捉到更丰富的语义关系,从而提升匹配的精度。尽管计算复杂度较高,但在高精度需求的场景中表现出色。
问题与挑战
尽管当前的模型在提升搜索相关性方面取得了显著进展,但仍面临一些重要的技术挑战:
-
长尾泛化效果存在瓶颈:在电商平台上,用户的搜索需求具有高度的多样性和个性化,特别是长尾搜索 query。这些长尾 query 往往缺乏足够的训练数据,导致模型在处理长尾需求时的泛化效果较差。
-
超长上下文理解有限:用户的搜索 query 有时包含复杂的上下文信息,特别是超长 query。现有模型在处理这些超长上下文时,理解能力有限,难以准确捕捉用户的真实意图,从而影响搜索结果的相关性。
基于大模型的解决方案
基于大模型的相关性提升方案逐渐成为研究热点。业界主要有两种主要的相关性提升方案:Prompt 工程应用结合数据增强蒸馏,以及增强预训练结合相关性对齐。
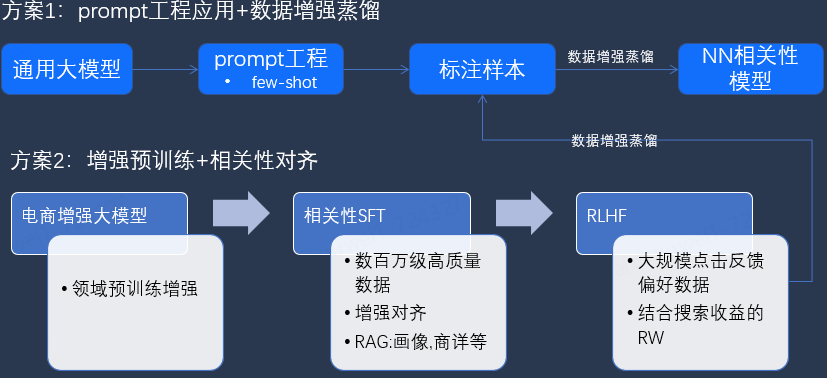
方案一:Prompt 工程应用 + 数据增强蒸馏
-
Prompt 工程应用 是一种通过设计和优化输入提示(prompts)来引导大模型生成更准确和相关的输出的方法。在电商搜索场景中,精心设计的 prompts 可以帮助模型更好地理解用户的搜索意图,而不需要后训练,从而提升搜索结果的相关性。
-
数据增强蒸馏 则是通过生成更多高质量的训练数据来提升模型的泛化能力。利用调试优化好的大模型 +prompt 工程来标注数据,再通过蒸馏技术将这些数据整合到模型的训练过程中。
通过结合 Prompt 工程和数据增强蒸馏,这一方案能够在有限的数据和算力条件下显著提升模型的搜索相关性,特别是在处理复杂和长尾 query 时表现尤为突出。
方案二:增强预训练 + 相关性对齐
-
增强预训练 是指在模型预训练阶段引入更多领域相关的数据和任务,以提升模型对特定领域的理解能力。在电商搜索场景中,可以通过引入大量商品描述、用户评论和搜索日志等数据进行预训练,使模型能够更好地理解商品和用户需求之间的关系。
-
相关性对齐 则是在模型训练过程中,通过设计特定的损失函数和优化策略,使得模型输出的相关性评分更符合实际需求。具体来说,可以通过引入多任务学习、对比学习等方法,使模型在学习商品相关性的同时,兼顾点击率(CRT)和转化率(CVR)等关键指标,核心是需要考虑搜索系统的收益。
5. 下一代 AI 电商搜索
在当前的电商系统中,无论是传统的货架电商还是新兴的内容电商,在整个购物消费链路中其核心驱动力依然是搜索和推荐技术。
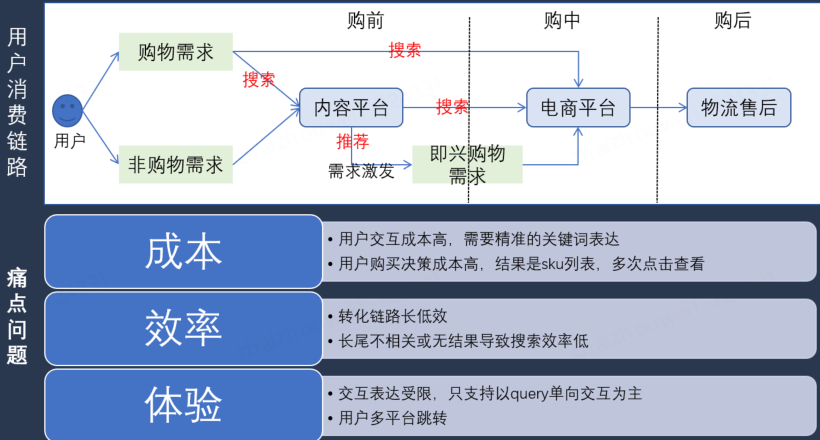
仍然面临着诸多痛点:
-
成本:用户交互成本高,需要精准的关键词表达才能容易找到所需商品,用户购买决策成本高,搜索结果通常是一个长长的 SKU 列表,用户需要多次点击查看商品详情,增加了决策难度和时间成本。
-
效率:传统搜推技术转化链路长且低效,长尾搜索结果不相关或无结果,导致搜索效率低下,用户难以找到符合需求的商品。
-
体验:交互方式受限,主要依赖于单向的 query 输入,会存在用户在多个平台之间跳转,增加了购物的复杂性和不便。
为了彻底解决这些痛点,理想的下一代 AI 电商搜索应在技术和产品形态上实现全面革新:
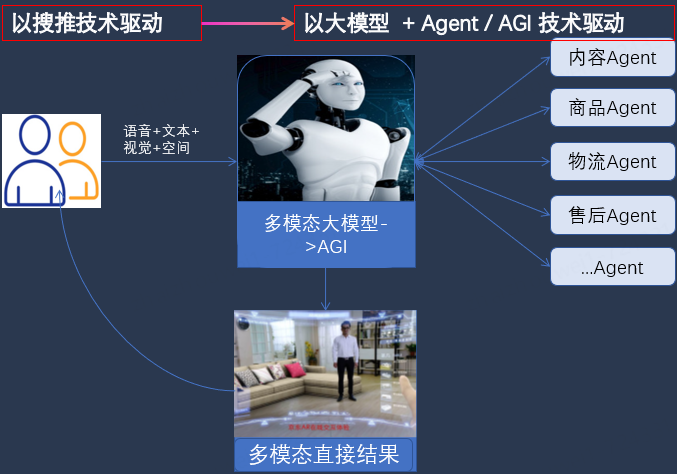
具体表现为以下几个方面:
-
技术驱动:下一代 AI 电商搜索应完全由大模型或 AGI 技术驱动。在技术上能够更深刻地理解用户需求,并提供高度个性化的搜索和推荐服务
-
数字虚拟助理:产品形态上,下一代 AI 电商搜索应类似于电影《Her》中出现的超级 AI 助手。这个数字虚拟助理能够与用户进行全模态的自然语言交互,包括无障碍的流畅语音交互,并且具备听觉、视觉和空间感知等能力。
-
精准商品推荐:基于用户需求,数字虚拟助理可以直接推荐最匹配的商品,并给出精准的商品总结,解释为什么这些商品满足用户需求,性价比如何等。对于需求不明的用户,助理可以进行拟人的交互式导购,帮助用户明确需求然后推荐。
-
智能代理:通过 AI Agent 技术,数字虚拟助理可以在用户授权下自动完成下单,包括后续的物流和售后服务。用户只需要下达简单的命令,助理即可完成整个购物流程,极大地简化了用户的操作。
下一代 AI 电商搜索不仅在技术上实现了从传统搜索到智能搜索的飞跃,更在用户体验上进行了全面的革新。通过大模型和 AGI 技术的驱动,结合数字虚拟助理的产品形态,用户将享受到更加精准、便捷和高效的购物体验,我想这应该是理想的 AI 电商搜索产品形态。
