免费做初中试卷的网站网站怎么做优化排名
关于rotated_rtmdet_l-coco_pretrain-3x-dota_ms.py配置文件的batchsize和学习率设置
问题:

回答:

如何在mmrotate中绘制特征图
问题:
回答:
你好@AllieLan,您可以尝试使用https://github.com/open-mmlab/mmyolo/blob/main/demo/featmap_vis_demo.py
[Feature] oriented reppoints 支持 filter_empty_gt=False 的训练
问题:

回答:

[1.x] RTMDet-R (tiny) 内存不足的 CUDA,具有 24GB VRAM 和 batch_size=1
问题:

回答:

如何在自己的数据集上测试大场景图片?
问题:
回答:
你好@TheGreatTreatsby, 你可以试试https://github.com/CAPTAIN-WHU/DOTA_devkit
请问这个项目中通道的ms+rr和论文中常说的多维度测试和多维度训练有什么区别
问题:

回答:
使用 DOTA V1.0 数据集时 CFA 重新分配过程中的张量不匹配错误
问题:

回答:


如何改变旋转框的定义范围(如何更改旋转框的定义范围)
问题:

回答:

如何获得精度和F1分数
问题:

回答:
在我的例子中,我修改了 eval_map.py 和我的 custumdataset.py
通过在 def eval_rbbox_map 中创建额外的变量来计算
cls_all_tp = np.sum(tp) cls_all_fp = np.sum(fp)
参考我项目的代码
我的项目

关于 R3Det 中的随机种子 #464
问题:




Question about random seed. #291

为什么相同的物体分类分数相差很大? #455
问题:



回答:

_base_ = ['./roi_trans_r50_fpn_1x_dota_le90.py']data_root = 'datasets/split_ms_dotav1/'
angle_version = 'le90'
img_norm_cfg = dict(mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
train_pipeline = [dict(type='LoadImageFromFile'),dict(type='LoadAnnotations', with_bbox=True),dict(type='RResize', img_scale=(1024, 1024)),dict(type='RRandomFlip',flip_ratio=[0.25, 0.25, 0.25],direction=['horizontal', 'vertical', 'diagonal'],version=angle_version),dict(type='PolyRandomRotate',rotate_ratio=0.5,angles_range=180,auto_bound=False,rect_classes=[9, 11],version=angle_version),dict(type='Normalize', **img_norm_cfg),dict(type='Pad', size_divisor=32),dict(type='DefaultFormatBundle'),dict(type='Collect', keys=['img', 'gt_bboxes', 'gt_labels'])
]
data = dict(train=dict(pipeline=train_pipeline,ann_file=data_root + 'trainval/annfiles/',img_prefix=data_root + 'trainval/images/'),val=dict(ann_file=data_root + 'trainval/annfiles/',img_prefix=data_root + 'trainval/images/'),test=dict(ann_file=data_root + 'test/images/',img_prefix=data_root + 'test/images/'))model = dict(train_cfg=dict(rpn=dict(assigner=dict(gpu_assign_thr=200))))检测细长物体的困难 #384
问题:
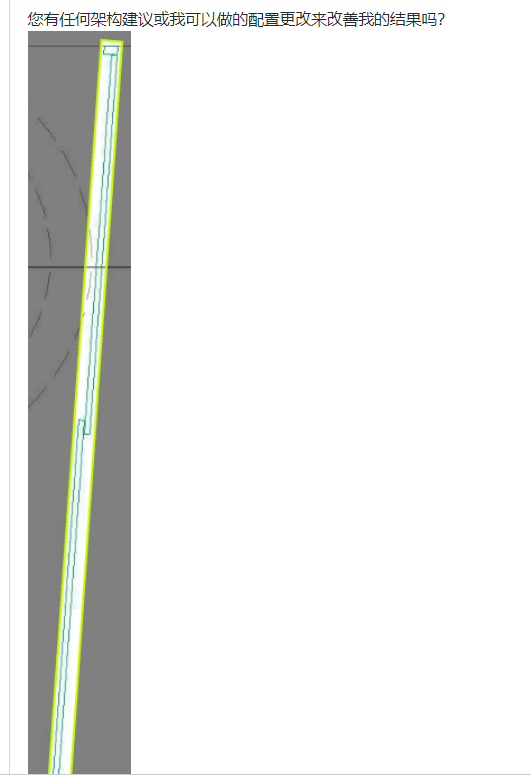
回答:

def gen_single_level_base_anchors(self,base_size,scales,ratios,center=None):"""Generate base anchors of a single level.Args:base_size (int | float): Basic size of an anchor.scales (torch.Tensor): Scales of the anchor.ratios (torch.Tensor): The ratio between between the heightand width of anchors in a single level.center (tuple[float], optional): The center of the base anchorrelated to a single feature grid. Defaults to None.Returns:torch.Tensor: Anchors in a single-level feature maps."""w = base_sizeh = base_sizeif center is None:x_center = self.center_offset * wy_center = self.center_offset * helse:x_center, y_center = centerh_ratios = torch.sqrt(ratios)w_ratios = 1 / h_ratiosif self.scale_major:ws = (w * w_ratios[:, None] * scales[None, :]).view(-1)hs = (h * h_ratios[:, None] * scales[None, :]).view(-1)else:ws = (w * scales[:, None] * w_ratios[None, :]).view(-1)hs = (h * scales[:, None] * h_ratios[None, :]).view(-1)# use float anchor and the anchor's center is aligned with the# pixel centerbase_anchors = [x_center - 0.5 * ws, y_center - 0.5 * hs, x_center + 0.5 * ws,y_center + 0.5 * hs]base_anchors = torch.stack(base_anchors, dim=-1)return base_anchorsHRSC2016 数据集性能重新实现 #202
问题:
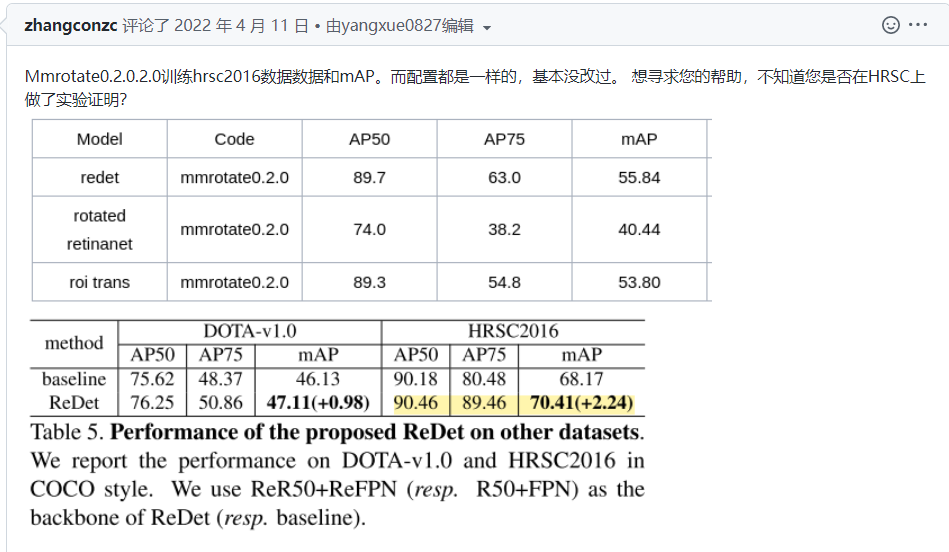
回答:
_base_ = ['../_base_/datasets/hrsc.py', '../_base_/schedules/schedule_3x.py','../_base_/default_runtime.py'
]angle_version = 'le90'
model = dict(type='ReDet',backbone=dict(type='ReResNet',depth=50,num_stages=4,out_indices=(0, 1, 2, 3),frozen_stages=1,style='pytorch',pretrained='./work_dirs/re_resnet50_c8_batch256-25b16846.pth'),neck=dict(type='ReFPN',in_channels=[256, 512, 1024, 2048],out_channels=256,num_outs=5),rpn_head=dict(type='RotatedRPNHead',in_channels=256,feat_channels=256,version=angle_version,anchor_generator=dict(type='AnchorGenerator',scales=[8],ratios=[0.5, 1.0, 2.0],strides=[4, 8, 16, 32, 64]),bbox_coder=dict(type='DeltaXYWHBBoxCoder',target_means=[.0, .0, .0, .0],target_stds=[1.0, 1.0, 1.0, 1.0]),loss_cls=dict(type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),roi_head=dict(type='RoITransRoIHead',version=angle_version,num_stages=2,stage_loss_weights=[1, 1],bbox_roi_extractor=[dict(type='SingleRoIExtractor',roi_layer=dict(type='RoIAlign', output_size=7, sampling_ratio=0),out_channels=256,featmap_strides=[4, 8, 16, 32]),dict(type='RotatedSingleRoIExtractor',roi_layer=dict(type='RiRoIAlignRotated',out_size=7,num_samples=2,num_orientations=8,clockwise=True),out_channels=256,featmap_strides=[4, 8, 16, 32]),],bbox_head=[dict(type='RotatedShared2FCBBoxHead',in_channels=256,fc_out_channels=1024,roi_feat_size=7,num_classes=1,bbox_coder=dict(type='DeltaXYWHAHBBoxCoder',angle_range=angle_version,norm_factor=2,edge_swap=True,target_means=[0., 0., 0., 0., 0.],target_stds=[0.1, 0.1, 0.2, 0.2, 0.1]),reg_class_agnostic=True,loss_cls=dict(type='CrossEntropyLoss',use_sigmoid=False,loss_weight=1.0),loss_bbox=dict(type='SmoothL1Loss', beta=1.0,loss_weight=1.0)),dict(type='RotatedShared2FCBBoxHead',in_channels=256,fc_out_channels=1024,roi_feat_size=7,num_classes=1,bbox_coder=dict(type='DeltaXYWHAOBBoxCoder',angle_range=angle_version,norm_factor=None,edge_swap=True,proj_xy=True,target_means=[0., 0., 0., 0., 0.],target_stds=[0.05, 0.05, 0.1, 0.1, 0.05]),reg_class_agnostic=False,loss_cls=dict(type='CrossEntropyLoss',use_sigmoid=False,loss_weight=1.0),loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))]),train_cfg=dict(rpn=dict(assigner=dict(type='MaxIoUAssigner',pos_iou_thr=0.7,neg_iou_thr=0.3,min_pos_iou=0.3,match_low_quality=True,ignore_iof_thr=-1),sampler=dict(type='RandomSampler',num=256,pos_fraction=0.5,neg_pos_ub=-1,add_gt_as_proposals=False),allowed_border=0,pos_weight=-1,debug=False),rpn_proposal=dict(nms_pre=2000,max_per_img=2000,nms=dict(type='nms', iou_threshold=0.7),min_bbox_size=0),rcnn=[dict(assigner=dict(type='MaxIoUAssigner',pos_iou_thr=0.5,neg_iou_thr=0.5,min_pos_iou=0.5,match_low_quality=False,ignore_iof_thr=-1,iou_calculator=dict(type='BboxOverlaps2D')),sampler=dict(type='RandomSampler',num=512,pos_fraction=0.25,neg_pos_ub=-1,add_gt_as_proposals=True),pos_weight=-1,debug=False),dict(assigner=dict(type='MaxIoUAssigner',pos_iou_thr=0.5,neg_iou_thr=0.5,min_pos_iou=0.5,match_low_quality=False,ignore_iof_thr=-1,iou_calculator=dict(type='RBboxOverlaps2D')),sampler=dict(type='RRandomSampler',num=512,pos_fraction=0.25,neg_pos_ub=-1,add_gt_as_proposals=True),pos_weight=-1,debug=False)]),test_cfg=dict(rpn=dict(nms_pre=2000,max_per_img=2000,nms=dict(type='nms', iou_threshold=0.7),min_bbox_size=0),rcnn=dict(nms_pre=2000,min_bbox_size=0,score_thr=0.05,nms=dict(iou_thr=0.1),max_per_img=2000)))img_norm_cfg = dict(mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
train_pipeline = [dict(type='LoadImageFromFile'),dict(type='LoadAnnotations', with_bbox=True),dict(type='RResize', img_scale=(800, 512)),dict(type='RRandomFlip', flip_ratio=0.5),dict(type='Normalize', **img_norm_cfg),dict(type='Pad', size_divisor=32),dict(type='DefaultFormatBundle'),dict(type='Collect', keys=['img', 'gt_bboxes', 'gt_labels'])
]
test_pipeline = [dict(type='LoadImageFromFile'),dict(type='MultiScaleFlipAug',img_scale=(800, 512),flip=False,transforms=[dict(type='RResize'),dict(type='Normalize', **img_norm_cfg),dict(type='Pad', size_divisor=32),dict(type='DefaultFormatBundle'),dict(type='Collect', keys=['img'])])
]dataset_type = 'HRSCDataset'
data_root = '/data/dataset_share/HRSC2016/HRSC2016/'
data = dict(samples_per_gpu=2,workers_per_gpu=2,train=dict(type=dataset_type,classwise=False,ann_file=data_root + 'ImageSets/trainval.txt',ann_subdir=data_root + 'FullDataSet/Annotations/',img_subdir=data_root + 'FullDataSet/AllImages/',pipeline=train_pipeline),val=dict(type=dataset_type,classwise=False,ann_file=data_root + 'ImageSets/test.txt',ann_subdir=data_root + 'FullDataSet/Annotations/',img_subdir=data_root + 'FullDataSet/AllImages/',pipeline=test_pipeline),test=dict(type=dataset_type,classwise=False,ann_file=data_root + 'ImageSets/test.txt',ann_subdir=data_root + 'FullDataSet/Annotations/',img_subdir=data_root + 'FullDataSet/AllImages/',pipeline=test_pipeline))evaluation = dict(interval=12, metric='mAP')
optimizer = dict(lr=0.01)
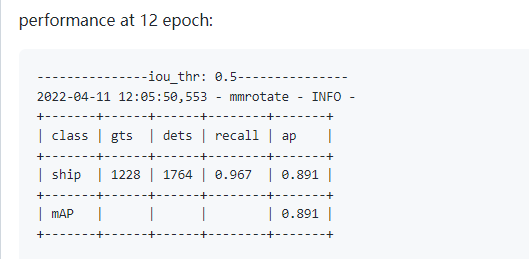


#原因是问题者的Target_stds和官方不一致,同时学习率也不一致导致的,官方也是使用单张GPU进行模型训练的。

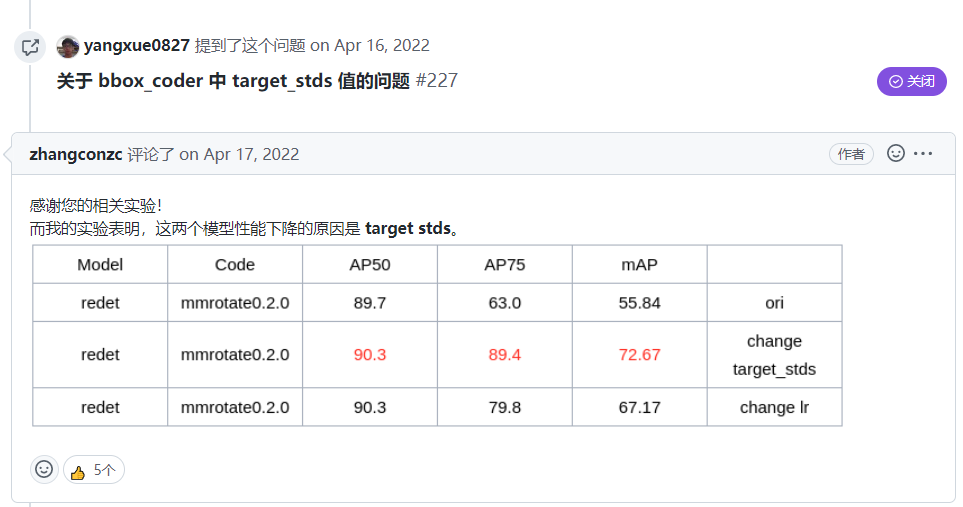
问题:

回答:
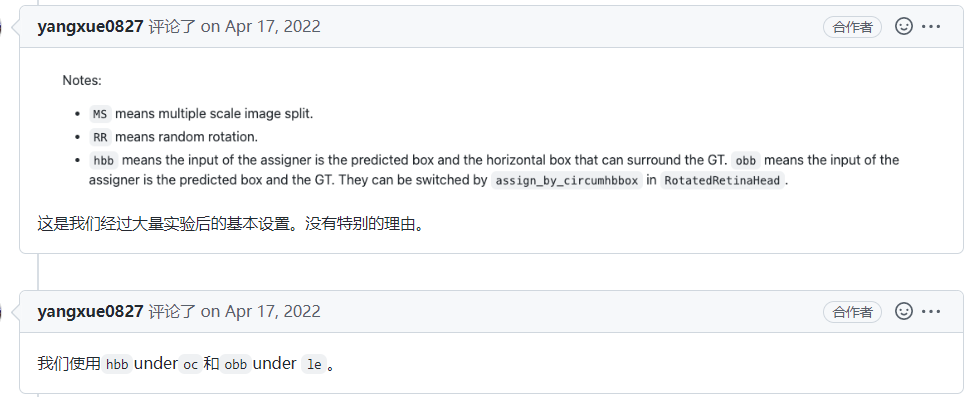
不同batchsize下s2anet的mAP #59




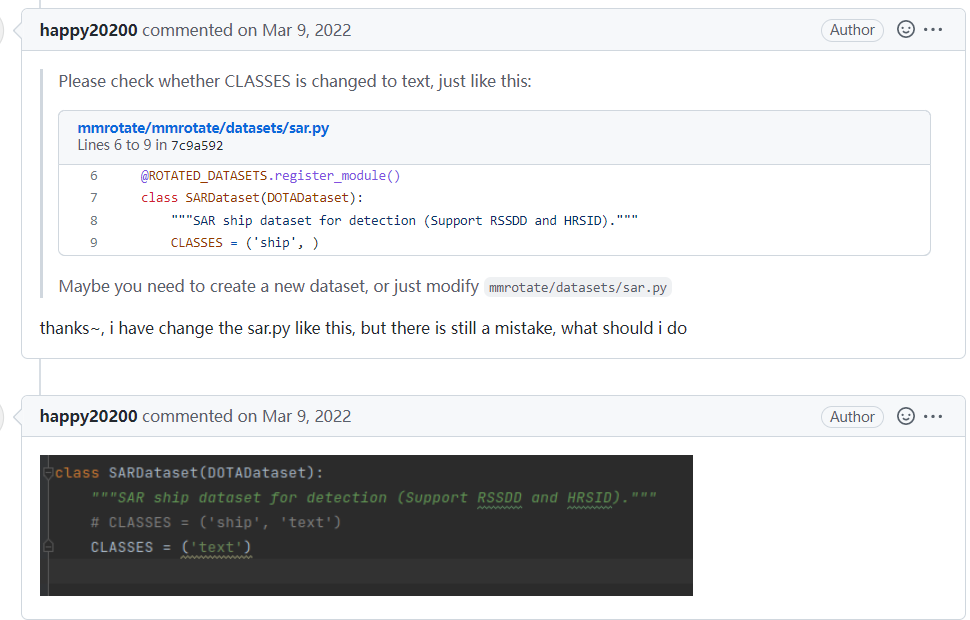
单个类别训练报错
问题:

回答:

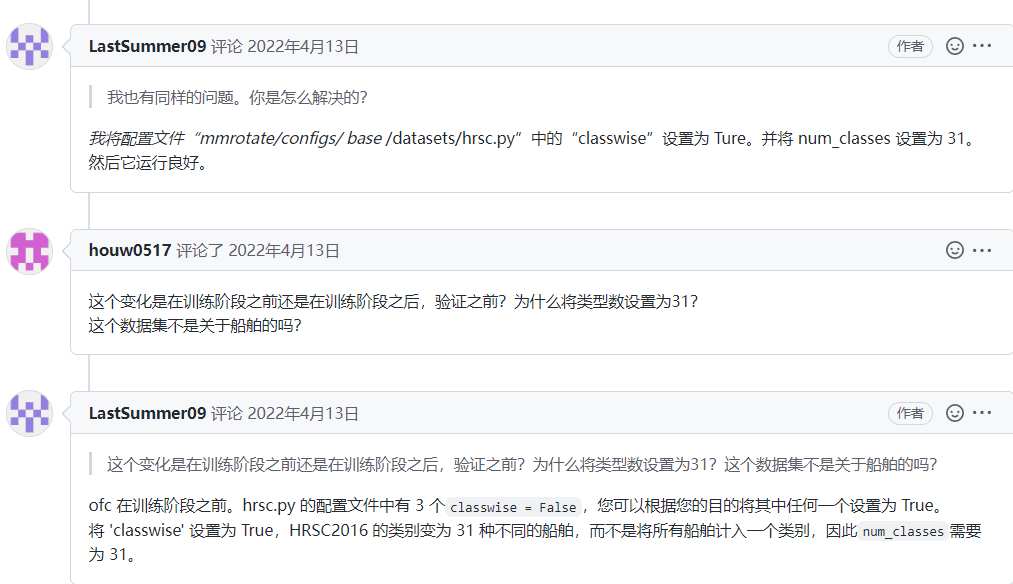
HRSC2016 的 classwise 设置为 True 时,在评估时出现“IndexError: tuple index out of range”。 #182

尝试结合 swin-Transform 和 s2anet #217
问题:

_base_ = ['./s2anet_r50_fpn_1x_dota_le135.py']pretrained = 'https://github.com/SwinTransformer/storage/releases/download/v1.0.0/swin_tiny_patch4_window7_224.pth' # noqamodel = dict(backbone=dict(_delete_=True,type='SwinTransformer',embed_dims=96,depths=[2, 2, 6, 2],num_heads=[3, 6, 12, 24],window_size=7,mlp_ratio=4,qkv_bias=True,qk_scale=None,drop_rate=0.,attn_drop_rate=0.,drop_path_rate=0.2,patch_norm=True,out_indices=(0, 1, 2, 3),with_cp=False,convert_weights=True,init_cfg=dict(type='Pretrained', checkpoint=pretrained)),neck=dict(_delete_=True,type='FPN',in_channels=[96, 192, 384, 768],out_channels=256,num_outs=5))optimizer = dict(_delete_=True,type='AdamW',lr=0.0001,betas=(0.9, 0.999),weight_decay=0.05,paramwise_cfg=dict(custom_keys={'absolute_pos_embed': dict(decay_mult=0.),'relative_position_bias_table': dict(decay_mult=0.),'norm': dict(decay_mult=0.)}))
数据标签过多次显示会爆炸、预测后不出指标结果;当数据标签过多时,显存会爆,预测后指标结果不显示; #333



一个对象在 oriented-reppoints 中有两个预测类 #426

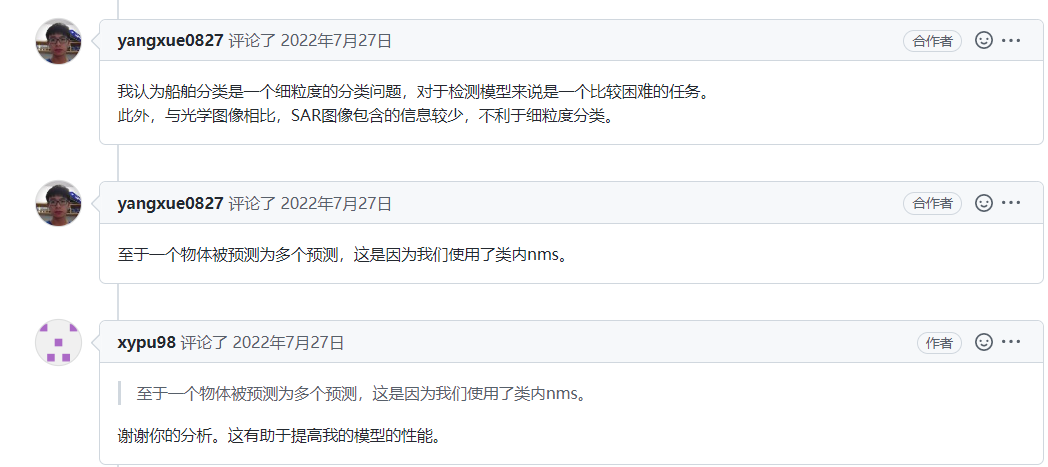
[文档]关于lr和batchsize的问题 #645

loss降不下来 #330


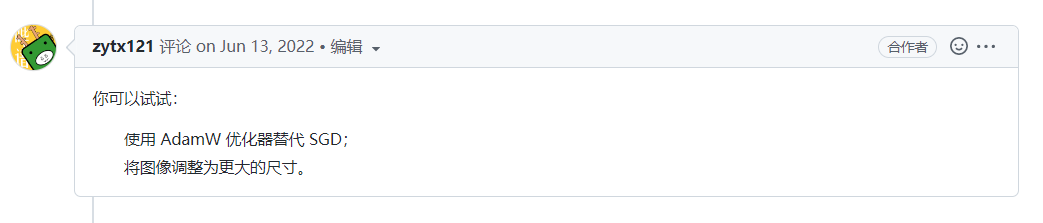
如何进行多尺度测试? #201

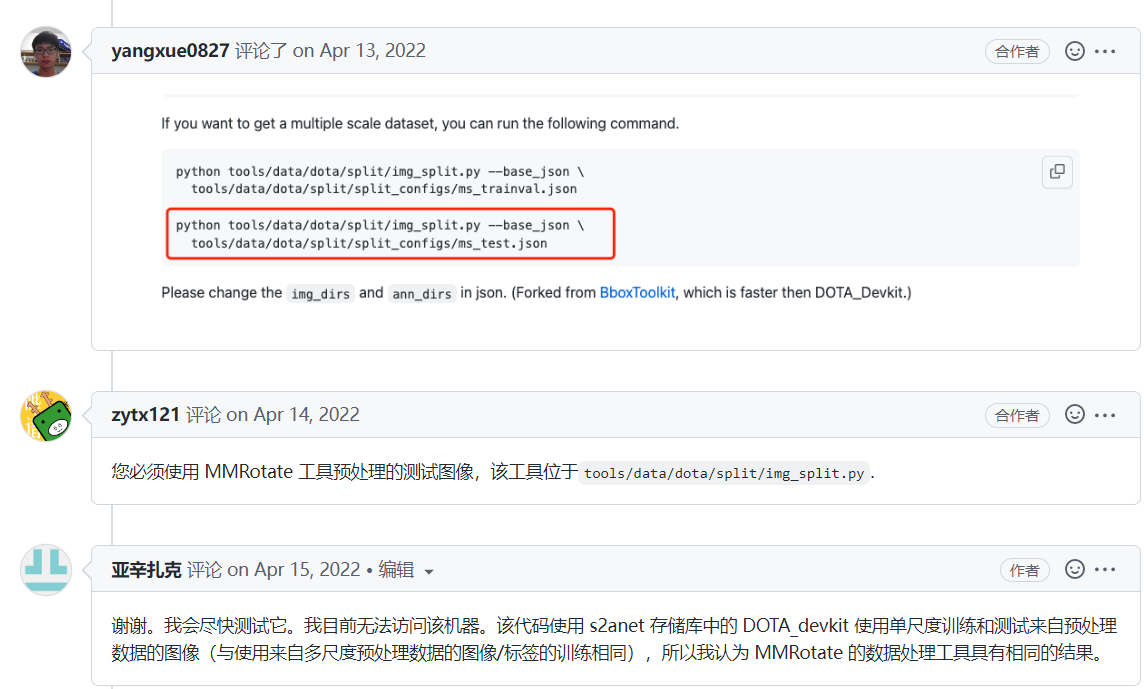
当我使用 rmosaic 时如何可视化 #686
你好@QAQTATQAQTAT,您可以使用demo/image_demo.py可视化 rmosaic 的输出。rmosaic的使用方法可以参考https://github.com/open-mmlab/mmrotate/blob/dev-1.x/configs/rotated_rtmdet/rotated_rtmdet_tiny-300e-aug-hrsc.py 。
Mosaic( img_scale=(1024, 1024))-> Resize(scale=(2048, 2048))->RandomCrop(crop_size=(1024, 1024))
train_pipeline = [dict(type='mmdet.LoadImageFromFile',file_client_args={{_base_.file_client_args}}),dict(type='mmdet.LoadAnnotations', with_bbox=True, box_type='qbox'),dict(type='ConvertBoxType', box_type_mapping=dict(gt_bboxes='rbox')),dict(type='mmdet.CachedMosaic',img_scale=(800, 800),pad_val=114.0,max_cached_images=20,random_pop=False),dict(type='mmdet.RandomResize',resize_type='mmdet.Resize',scale=(1600, 1600),ratio_range=(0.5, 2.0),keep_ratio=True),dict(type='RandomRotate', prob=0.5, angle_range=180),dict(type='mmdet.RandomCrop', crop_size=(800, 800)),dict(type='mmdet.YOLOXHSVRandomAug'),dict(type='mmdet.RandomFlip',prob=0.75,direction=['horizontal', 'vertical', 'diagonal']),dict(type='mmdet.Pad', size=(800, 800), pad_val=dict(img=(114, 114, 114))),dict(type='mmdet.CachedMixUp',img_scale=(800, 800),ratio_range=(1.0, 1.0),max_cached_images=10,random_pop=False,pad_val=(114, 114, 114),prob=0.5),dict(type='mmdet.PackDetInputs')
][WIP] 在 TRR360D 中支持 RR360(旋转矩形 360)检测 #731
https://github.com/open-mmlab/mmrotate/pull/731
Oriented RCNN 不支持 iou loss? #649



如何训练宽高比大的物体 #285


