手机网站模板 html5个人网站赚广告费
Redis 不仅仅是一个数据库,还可以作为支持发布和订阅(Pub/Sub)操作的消息代理。本文将使用 Navicat for Redis 简要概述 Redis 的 Pub/Sub 功能。
关于发布或订阅消息范式
Pub/Sub 是一种模式,发送者(广播者)不能向特定接收者(订阅者)发送消息。相反,发布的消息以频道形式发送,并且发送者不知道有多少订阅者正在订阅这个频道。而订阅者可以订阅一个或多个频道,以便只接收他们感兴趣的消息。以这种方式对发布者和订阅者进行解构能提高可扩展性,并更容易管理复杂系统中的信息流。
Redis Pub/Sub 提供了一种轻量级、快速、可扩展的消息解决方案,可用于各种目的,例如实时通知,在微服务之间发送消息或在单个应用程序的不同部分之间进行通信。
Redis中的消息传递
Redis 采用最多一次消息传递系统。顾名思义,消息只会被传递一次。因此,一旦 Redis 服务器发送消息,就不会再次发送。如果订阅者无法接收消息(例如,由于错误或网络中断),则消息将永远丢失。就像在收音机上收听你最喜欢的节目一样,如果错过了,就没有机会再听到。如果你的应用程序需要更强的传递保证,你应该使用 Redis Streams。
此外,Pub/Sub 与键空间无关。这意味着在数据库 10 上发布的消息能被数据库 1 上的订阅者接收到。如果你需要范围界定,Redis 建议在頻道名加上前缀(即 prod_mychannel,test_mychannel)。
使用 Navicat for Redis 发布消息
在 Navicat for Redis(或Navicat Premium)中,我们可以通过主工具栏上的 Pub/Sub 按钮打开 Pub/Sub 画面。我们可以在那里使用“发布窗格”发布消息:
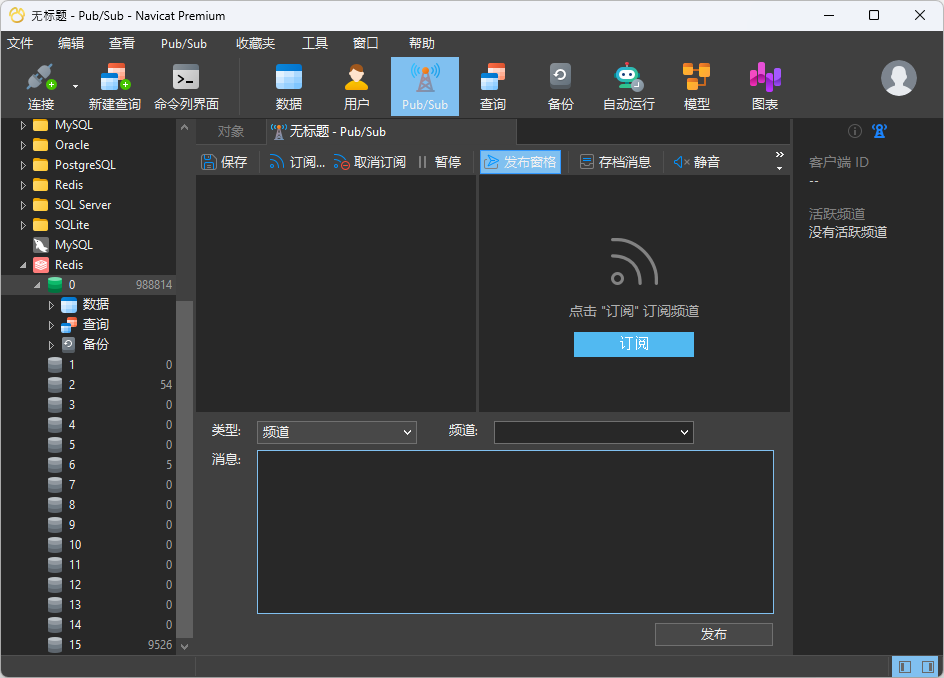
在 Redis 中,频道不是由用户创建的。当发布第一条消息或客户端订阅时,频道会自动创建。为了演示,我们将使用同一个 Redis 服务器创建两个连接。每个连接将充当不同的客户端。第一个连接将订阅“test_channel”,而第二个连接将向同一频道发布消息。这样做,我们希望消息在发布后能立即传递给订阅者。
在 Navicat 中订阅频道,我们只需要点击“订阅”按钮即可。这将打开“订阅”对话框:
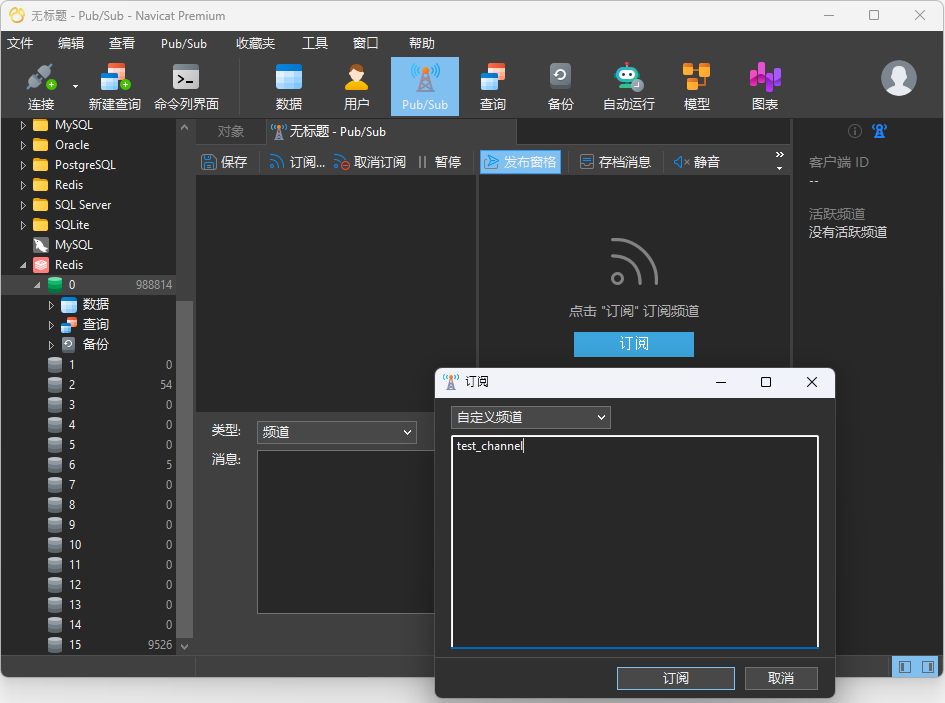
在这里,我们将输入频道名称“test_channel”,然后点击“订阅”。对话框关闭后,频道将出现在“频道”列表中,并记录订阅操作:
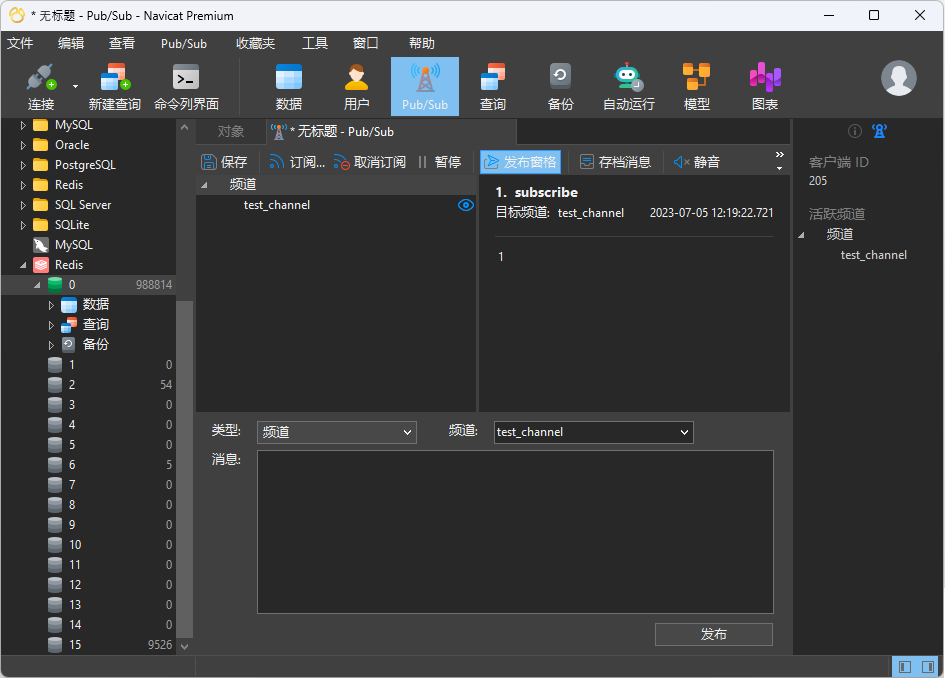
如果要在 Navicat 中发布消息,我们将在“频道”列表中选择一个频道(由于我们此时只有一个通道,因此是默认选项),然后在“消息”文本字段中输入消息,点击“发布”。此时,我们应该看到收到消息的通知:

总结
本文使用 Navicat for Redis 简要介绍了 Redis 的 Pub/Sub 功能。如果你有兴趣试用 Navicat for Redis,可以在 此处 下载。试用版具备完整功能,试用期为 14 天。
相关技术文章
开始使用 Redis
Navicat for Redis 功能介绍
Redis 数据类型
如何在 Redis 中处理键值
Redis Pub/Sub 指南
Redis 列表 | 概述
