东台建设网站的公司垫江网站建设价格
数据集格式:Pascal VOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)
图片数量(jpg文件个数):7559
标注数量(xml文件个数):7559
标注数量(txt文件个数):7559
标注类别数:4
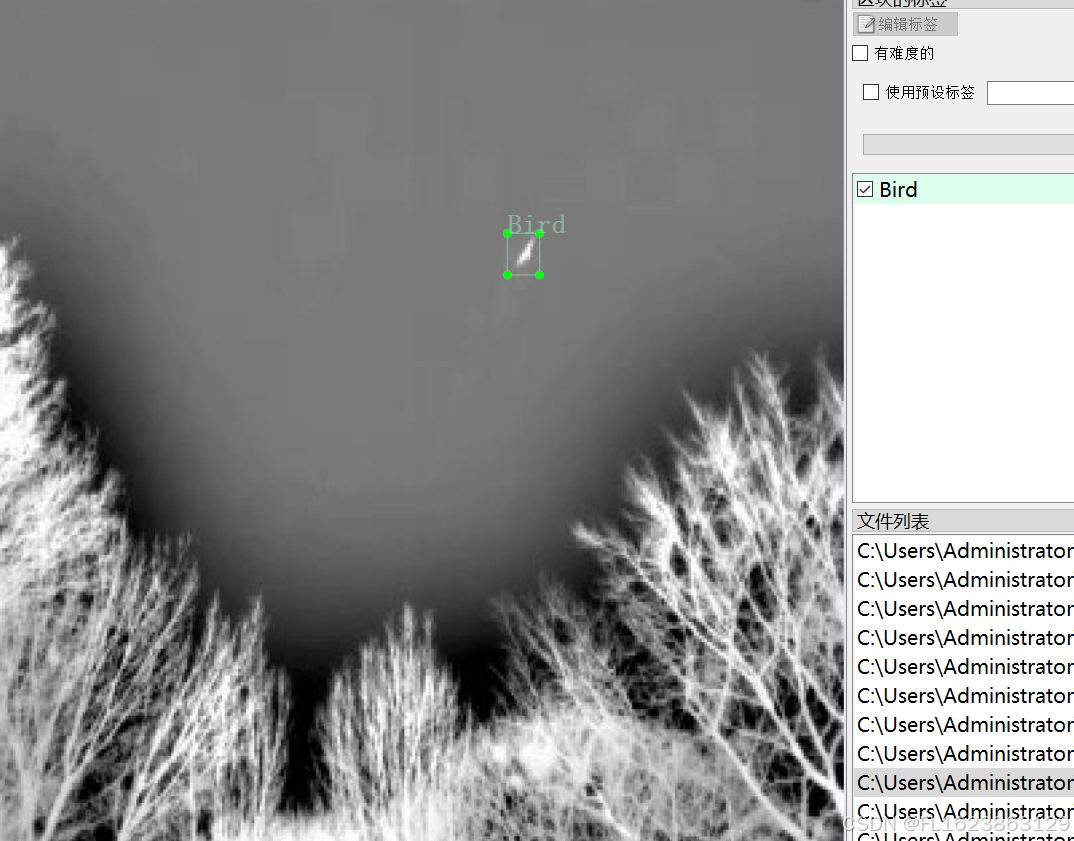
标注类别名称:["Airplane","Bird","Drone","Helicopter"]
每个类别标注的框数:
Airplane 框数 = 971
Bird 框数 = 1214
Drone 框数 = 4242
Helicopter 框数 = 1431
总框数:7858
使用标注工具:labelImg
标注规则:对类别进行画矩形框
重要说明:暂无
特别声明:本数据集不对训练的模型或者权重文件精度作任何保证,数据集只提供准确且合理标注
该数据集经过yolov8训练,表明数据集不存在问题,具体训练指标参数参考博文:基于yolov8的红外小目标无人机飞鸟检测系统python源码+onnx模型+评估指标曲线+精美GUI界面-CSDN博客
图片预览:

标注例子:


下载地址:https://download.csdn.net/download/FL1623863129/89767353
