微网站下载资料怎么做自己做网站要钱吗
背景
IntelliJ IDEA中的Scratches and Consoles是一种临时的文件编辑环境,用于写一些文本内容或者代码片段。
其中,Scratch files拥有完整的运行和debug功能,这些文件需要指定编程语言类型并且指定后缀。
举例:调接口
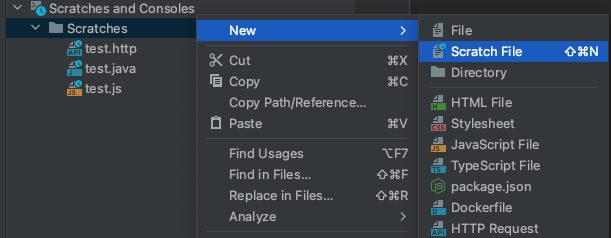
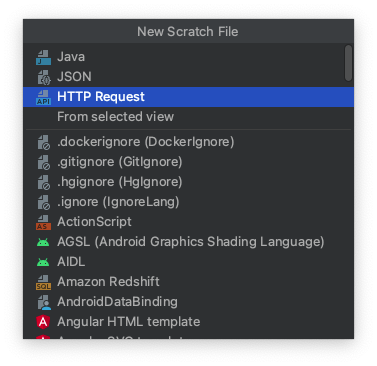
可以看到有很多语言选项,比如我们这里想用 http 请求我们编写的 java 接口
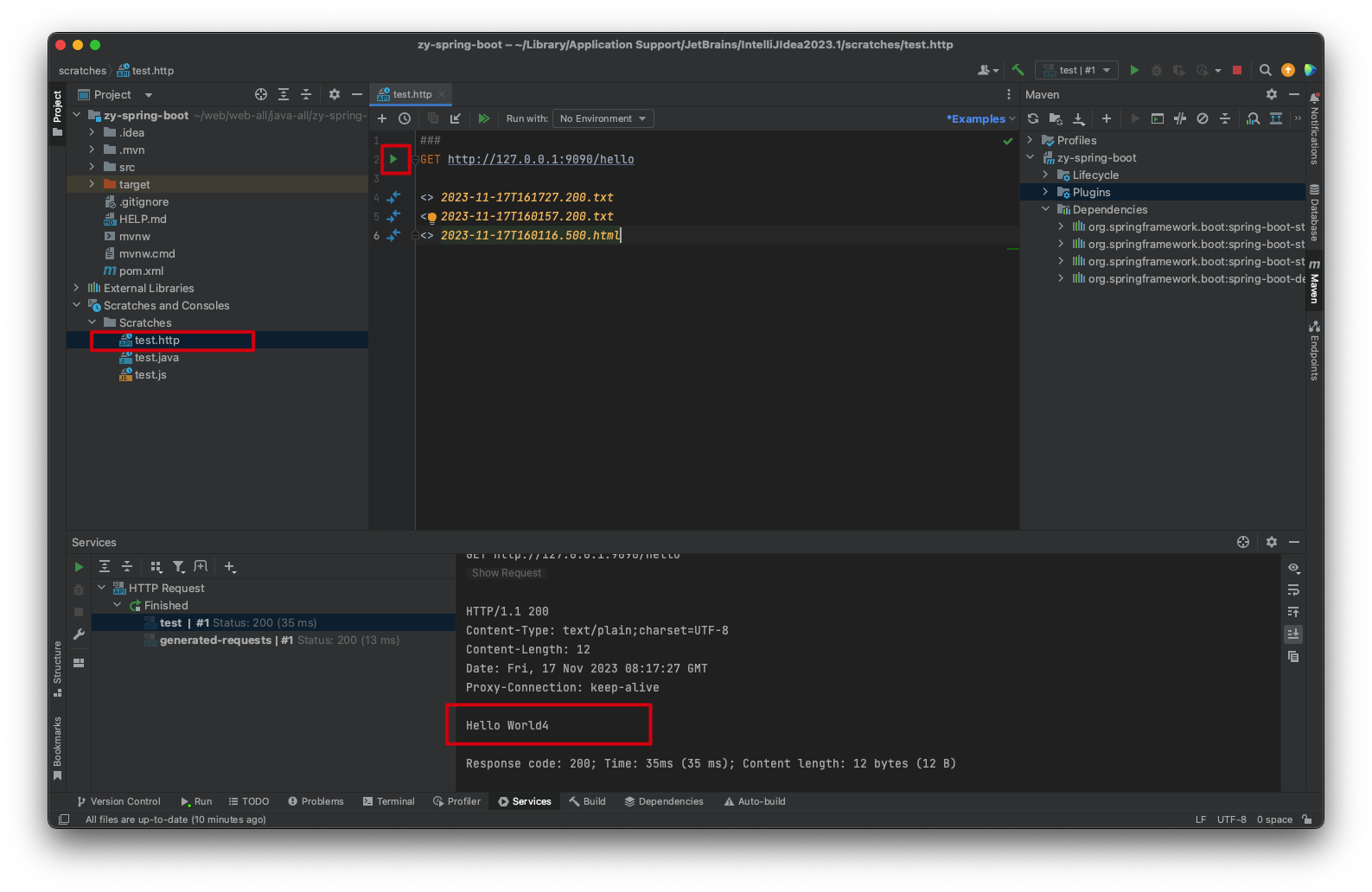
这样就可以不用打开 postman 了,方便很多。
举例:快速启动一个java程序
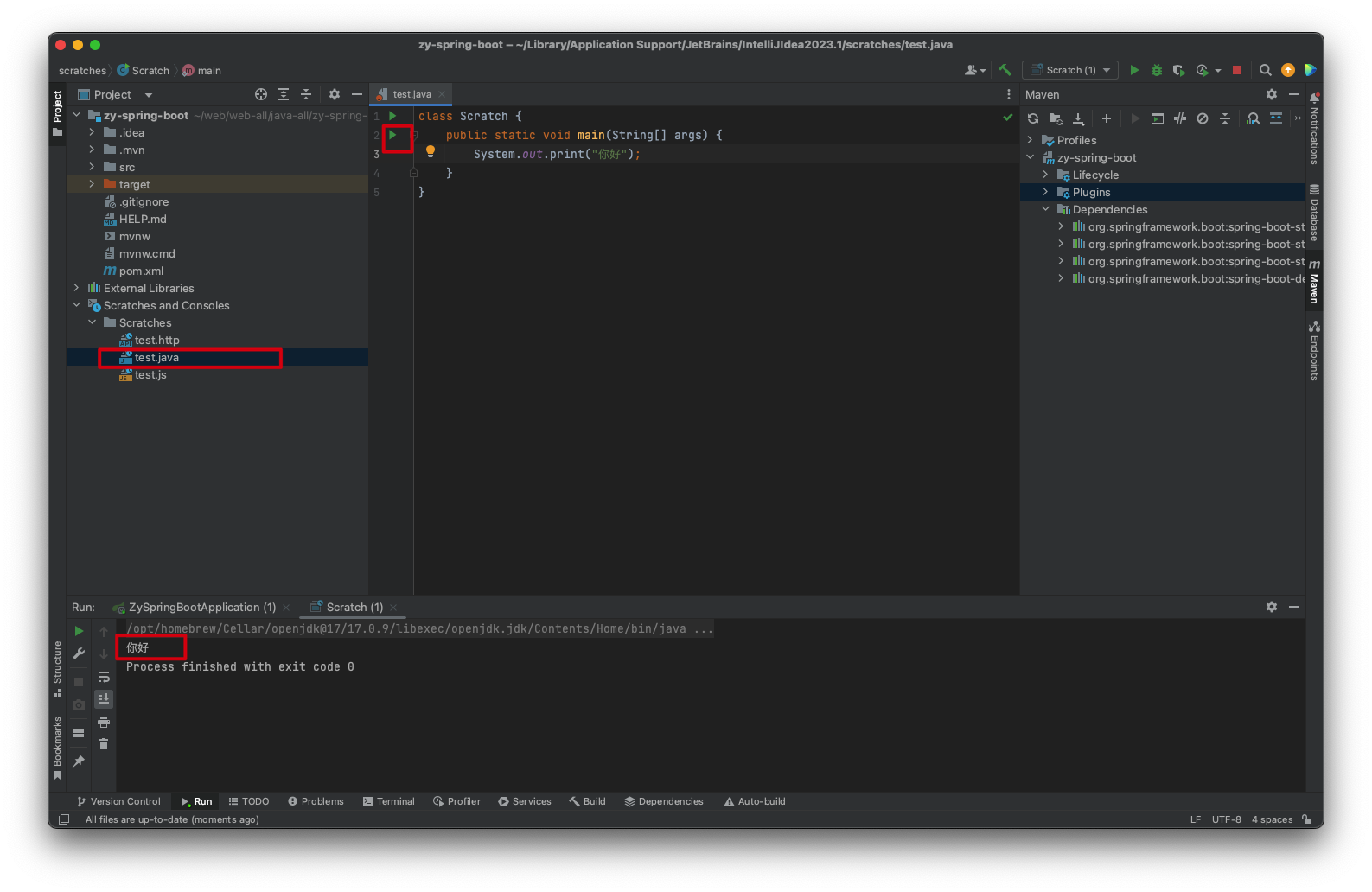
举例:快速启动一个js程序
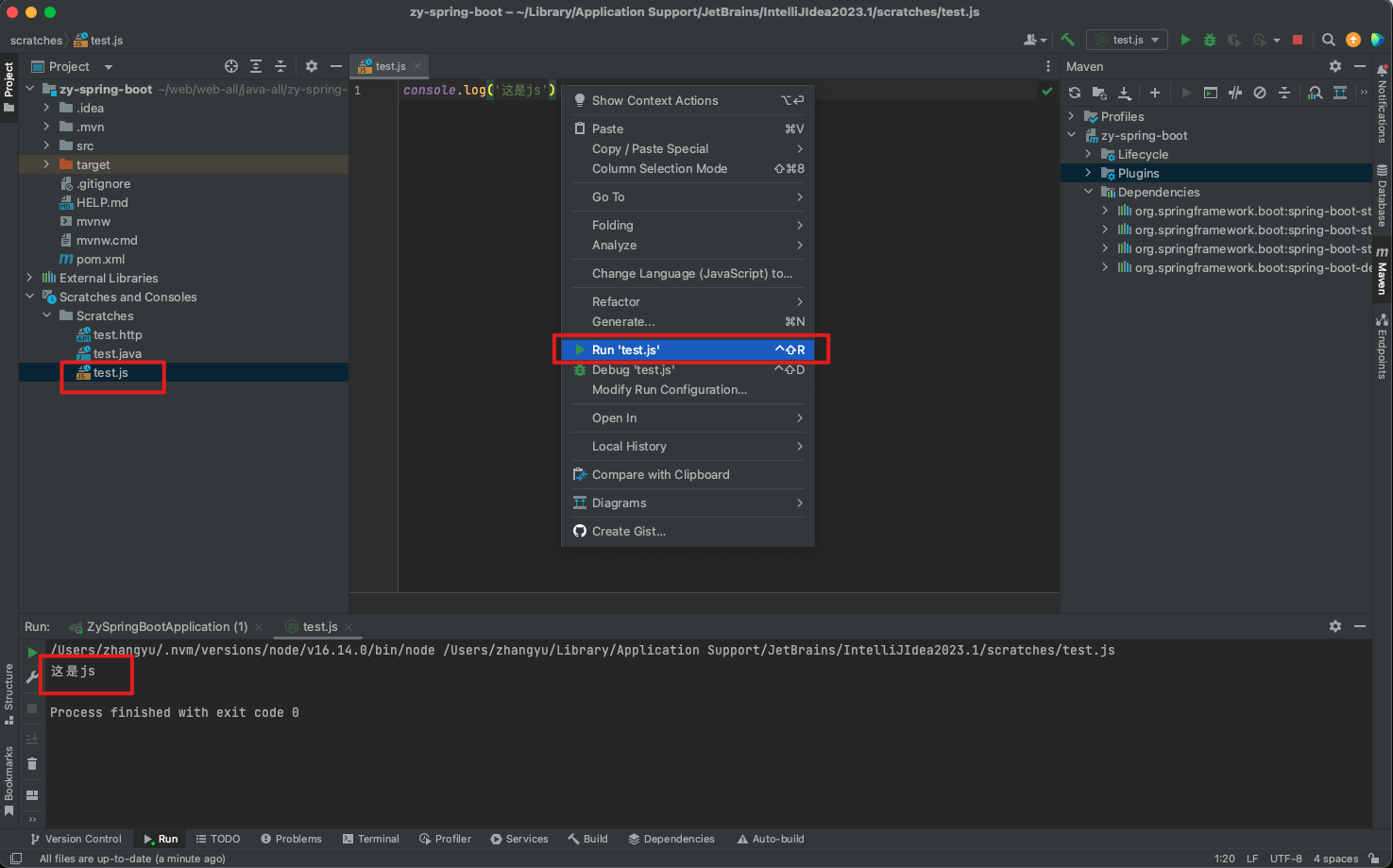
具体这些文件保存的位置可以右键查看哦,我的是在:/Users/zhangyu/Library/Application Support/JetBrains/IntelliJIdea2023.1/scratches/test.http
最后
这些文件是只读的,不能被保存为项目的一部分,也不能被多人协作。它们通常用于存储一些临时的想法、代码片段或测试数据,不会被永久保存。
因此,如果你想在多个会话之间保留Scratch File的内容,你可能需要考虑将其导出到其他位置,或者使用其他工具来进行长期存储。
