建设一个购物网站需要什么意思培训机构的网站建设
个人博客地址:www.jiasun.top
使用github page+hexo搭建,主题为fluid,搭建步骤参照:Github + hexo 实现自己的个人博客、配置主题(超详细)
主题:https://hexo.fluid-dev.com/
搭建时的问题:
1 Ubuntu apt默认下载的nodejs版本过低,snap安装18.18的node js
2 在source目录下添加CNAME文件指定个人域名
3 在iconfont中搜索所需图标,并通过自定义css导入项目 自定义图标
4 在source目录下添加本地图片以便博客引用
5 通过CsdnSyncHexo将csdn博客导出为markdown格式并移至source/_posts目录下
6 csdn博客迁移后图片显示403, 只需要在每个文章的头部加上这么一句代码就可以 <meta name="referrer" content="no-referrer" />
Hexo 搭建:图片不能正常显示问题(简书图片403)
该语句能生效的原因:
http请求头中有一个referrer字段,用来表示发起http请求的源地址信息
服务器端在拿到这个referrer值后判断请求是否来自本站
若不是则返回403,从而实现图片的防盗链。上面出现403就是因为,请求的是别人服务器上的资源,但把自己的referrer信息带过去了,被对方服务器拦截返回了403
在前端可以通过meta来设置referrer policy(来源策略),referrer设置成no-referrer,发送请求不会带上referrer信息,对方服务器也就无法拦截了
get请求图片出现403 防盗链解决方式 no-referrer
通过vscode替换功能一次性更新所有博客md文件
---<!--more--># 换成---
<meta name="referrer" content="no-referrer" />
<!--more-->
7 csdn导出的markdown文件toc目录未能正常显示,文章开头没有以下类似的东西,只显示一个TOC字符

但发现侧边栏也有目录,故删去TOC语句

通过vscode正则匹配一次性删去所有TOC行
^.*(@[TOC]).*\n
VSCode 批量删除指定匹配的一整行
8 导出的markdown文件分类以空格分割,需手动改成-[]分割
categories: 踩坑日记 源码剖析 内核驱动开发记录# 改成categories:
- [踩坑日记]
- [源码剖析]
- [内核驱动开发记录]
分类和标签
9 代码风格改成atom-one-dark
highlightjs:# 在链接中挑选 style 填入# Select a style in the link# See: https://highlightjs.org/static/demo/style: "atom-one-dark"style_dark: "atom-one-dark"
https://highlightjs.org/demo
好像要npm install highlightjs --save
10 添加音乐播放器
在网易云得到外链
<iframe frameborder="no" border="0" marginwidth="0" marginheight="0" width=330 height=86 src="//music.163.com/outchain/player?type=2&id=65800&auto=1&height=66"></iframe>
在node_modules/hexo-theme-fluid/layout/about.ejs中加入
<div class="music-player"><iframe frameborder="no" border="0" marginwidth="0" marginheight="0" width=330 height=86 src="//music.163.com/outchain/player?type=2&id=65800&auto=1&height=66"></iframe>
</div>
可以通过修改node_modules/hexo-theme-fluid/修改页面信息
最终效果:
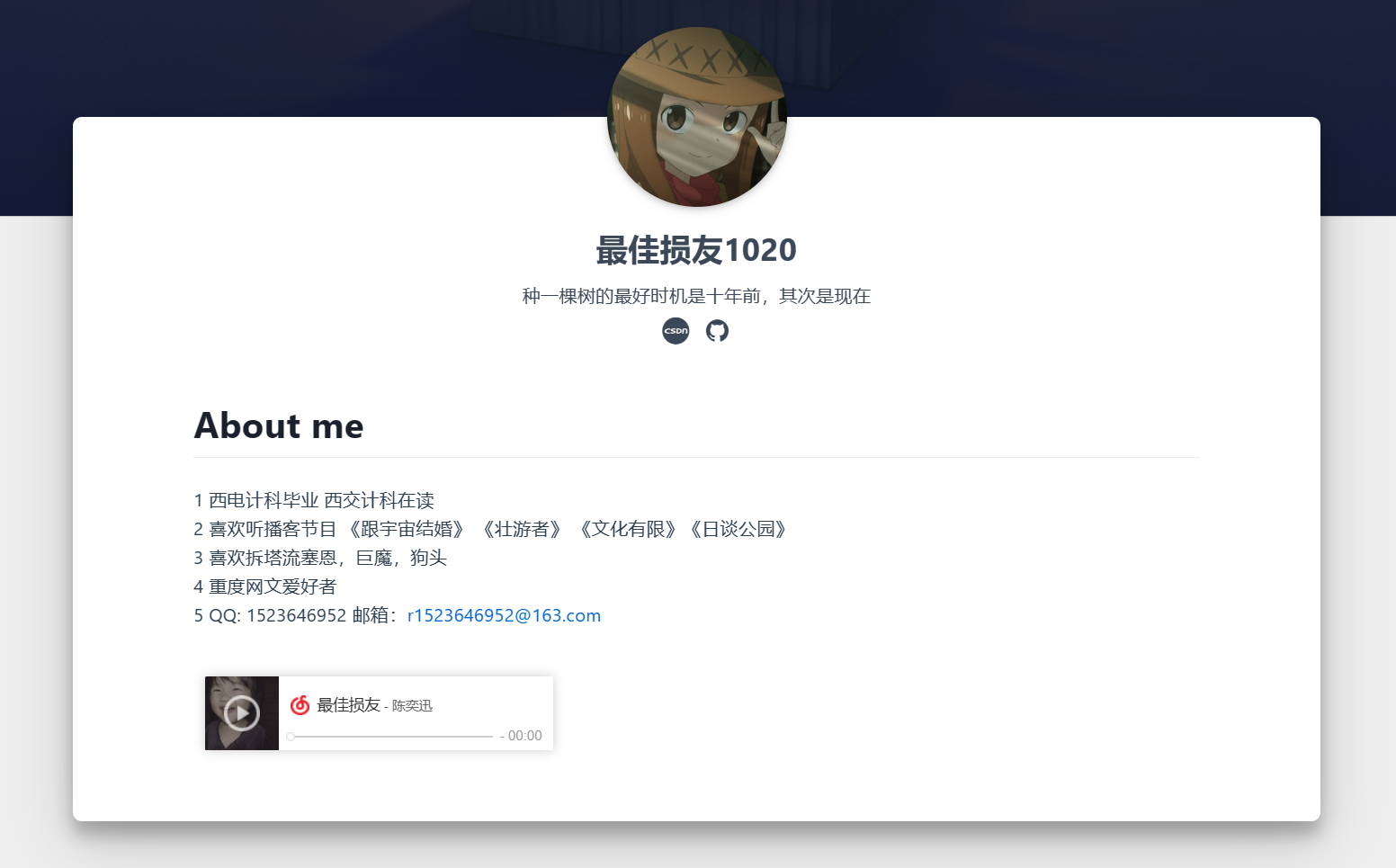
目录结构

hexo 第四讲 – 界面中加入音乐
TODO:
- 增加评论功能
- 增加访问统计功能
- seo优化
- 美化界面
