百度 新网站 重定向过多丹东seo优化
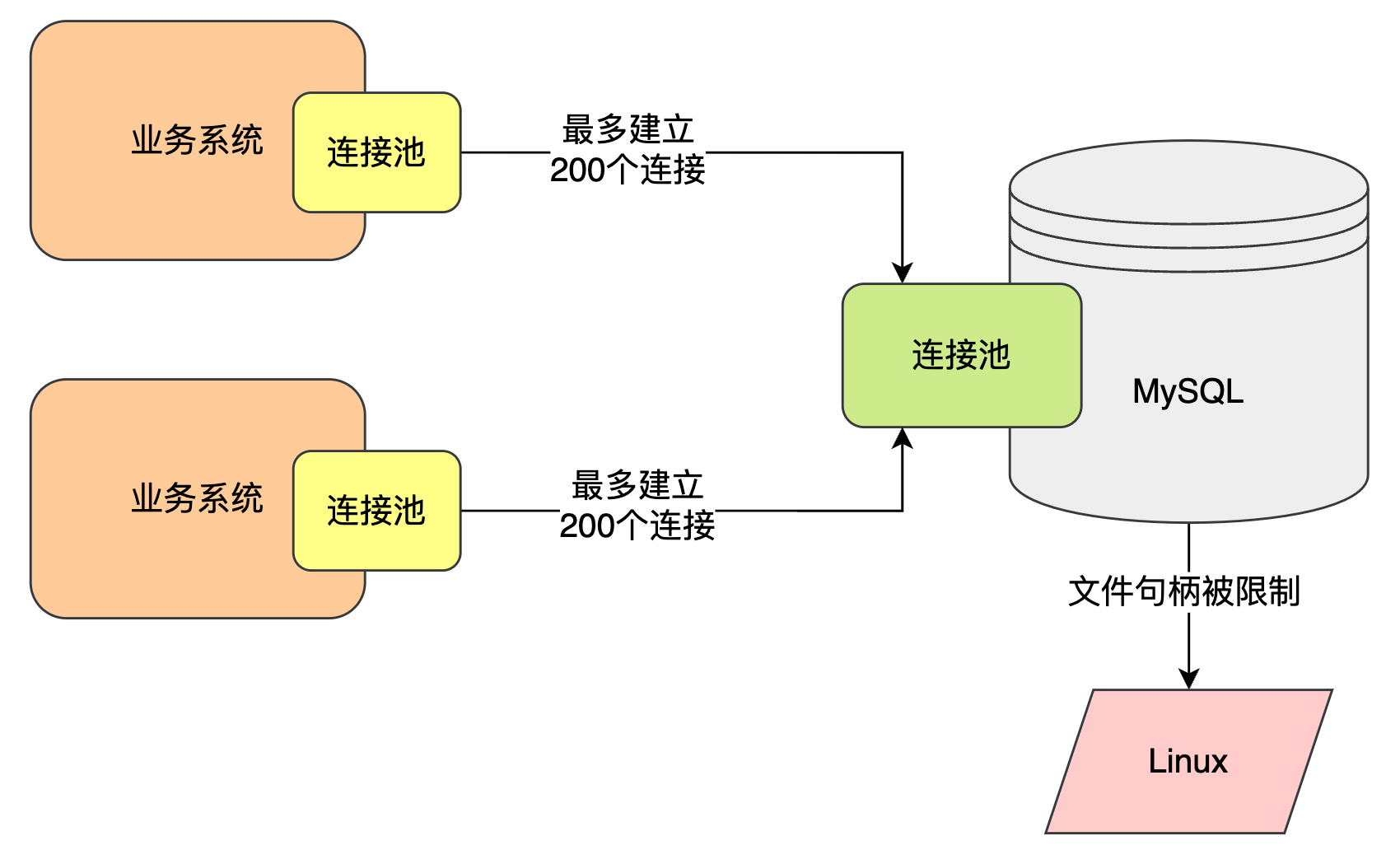
今天我们继续讲解昨天的那个案例背景,其实就是经典的Too many connections故障,他的核心就是linux的文件句柄限制,导致了MySQL的最大连接数被限制,那么今天来讲讲怎么解决这个问题。
其实核心就是一行命令:
ulimit -HSn 65535
然后就可以用如下命令检查最大文件句柄数是否被修改了
cat /etc/security/limits.conf
cat /etc/rc.local
-
如果都修改好之后,可以在MySQL的my.cnf里确保max_connections参数也调整好了;
-
然后可以重启服务器,然后重启MySQL;
-
这样的话,linux的最大文件句柄就会生效了,MySQL的最大连接数也会生效了。
-
然后此时你再尝试业务系统去连接数据库,就没问题了!
另外再给大家解释一个问题,有人还是疑惑说,为什么linux的最大文件句柄限制为1024的时候,MySQL的最大连接数是214呢?
这个其实是MySQL源码内部写死的,他在源码中就是有一个计算公式,算下来就是如此罢了!
然后再给大家说一下,这个linux的ulimit命令是干嘛用的,其实说白了,linux的话是默认会限制你每个进程对机器资源的使用的,包括可以打开的文件句柄的限制,可以打开的子进程数的限制,网络缓存的限制,最大可以锁定的内存大小。
因为linux操作系统设计的初衷,就是要尽量避免你某个进程一下子耗尽机器上的所有资源,所以他默认都是会做限制的。
那么对于我们来说,常见的一个问题,其实就是文件句柄的限制。
因为如果linux限制你一个进程的文件句柄太少的话,那么就会导致我们没办法创建大量的网络连接,此时我们的系统进程就没法正常工作了。
举个例子,比如MySQL运行的时候,其实就是linux上的一个进程,那么他其实是需要跟很多业务系统建立大量的连接的,结果你限制了他的最大文件句柄数量,那么他就不能建立太多连接了!
所以说,往往你在生产环境部署了一个系统,比如数据库系统、消息中间件系统、存储系统、缓存系统之后,都需要调整一下linux的一些内核参数,这个文件句柄的数量是一定要调整的,通常都得设置为65535
还有比如Kafka之类的消息中间件,在生产环境部署的时候,如果你不优化一些linux内核参数,会导致Kafka可能无法创建足够的线程,此时也是无法运行的。
所以我们平时可以用ulimit命令来设置每个进程被限制使用的资源量,用ulimit -a就可以看到进程被限制使用的各种资源的量。
比如 **core file size **代表的进程崩溃时候的转储文件的大小限制,max locked memory就是最大锁定内存大小,open files就是最大可以打开的文件句柄数量,max user processes就是最多可以拥有的子进程数量。
设置之后,我们要确保变更落地
cat /etc/security/limits.conf
cat /etc/rc.local
