温州网站建设的公司wordpress 猫
一、概述(Overview)
蓝牙是一种专有的开放式无线技术标准,用于在固定和移动设备之间进行短距离数据交换(使用2400–2480 MHz ISM波段的短波长无线电传输),从而创建具有高度安全性的个人局域网(PANs)。由电信供应商爱立信(telecoms vendor Ericsson)于1994年创建,[1]最初被认为是RS-232数据电缆的无线替代品(wireless alternative)。它可以连接多个设备,从而克服同步(synchronization)问题。
二、蓝牙框架和代码目录
以高通项目举例
下图介绍了 Qualcomm BT 的架构。
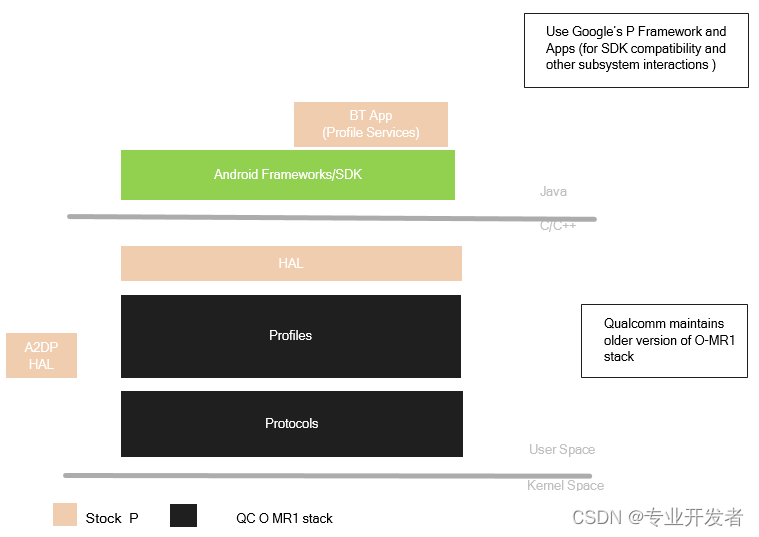
下面的表格介绍了 Qualcomm BT 的代码各个目录
| 蓝牙code目录 | |
| packages/apps/Bluetooth | Bluetooth |
| frameworks/base/core/java/android/bluetooth | Bluetooth service层 |
| frameworks/base/media/packages/BluetoothMidiService | |
| frameworks/base/core/proto/android/bluetooth | |
| external/libchrome/device/bluet |
