什么网站吸引流量wordpress网站备份恢复
在之前的网络基础博客中,我们对网络的基本概念进行了一个简单的介绍,那么接下来的网络内容中,我们将对网络通信中的典型协议进行详细解释。
我们根据网络协议中的分层来对典型协议进行注意介绍,不过对于物理层的传输我们不做考究,我们只从软件层面入手。接下来我们从应用层出发,讲述它的典型协议。
目录
1.应用层传输
1.1自定制协议
1.2HTTP协议
1.2.1内容
1.2.2特性
1.2.3格式
1.2.4Cookie
1.3HTTPS协议
1.应用层传输
应用层是负责应用程序之间的数据沟通,是一种面向程序员的协议。因为应用程序都是由程序员设计,所以它们之间的数据沟通也由程序员来设计完成。而其中一些协议的设计,在针对某些场景时,有很好的使用效果,并且使用人数较多。我们把这种协议称为知名协议。
1.1自定制协议
自定制协议时程序员自己定义的程序沟通数据格式约定,在我们设计自定制协议时,肯定需要就某些要素进行考虑,使得通向传输更加稳定,便捷和快速。
不过在了解这些要素之前,我们需要明白数据的序列化和反序列化的大致内容。对于序列化指的是,在网络传输或数据的持久化存储中,将多个数据对象按照指定格式组织成为一个二进程文件,进行传输或持久化存储的一个过程;对于反序列化指的是,对二进程数据进行指定格式的解析,得到各个数据对象内容的一个过程。
那么对于我们设计自定制协议需要考虑的要素内容便是:
- 传输性能:定制一个协议,传输的数据需要尽可能小(不影响表达),助于提高传输速度;
- 解析性能:传输和接收多个数据对象的时进行序列化和反序列化需要尽可能简单快捷;
- 调试便捷性:对于不同的程序员而言,拥有较好的可见性和可识别性。
在大致了解完毕自定制协议的内容之后,我们来讲述一些知名协议的内容。
1.2HTTP协议
1.2.1内容
HTTP协议是一种超文本传输协议,是现在互联网公司中使用最多的协议,它早期是用来传输web网页所设计的协议。
1.2.2特性
HTTP存在三点特性,即:
- 基于字符串明文传输,调试便捷性高;
- 是一种简单的请求--响应协议;(早期是短链接--一次请求响应结束后便关闭)
- 基于TCP协议传输,安全可靠。
1.2.3格式
HTTP的请求格式(请求报文)分为四部分,分别是:请求行(首行)、请求头部、空行和正文。
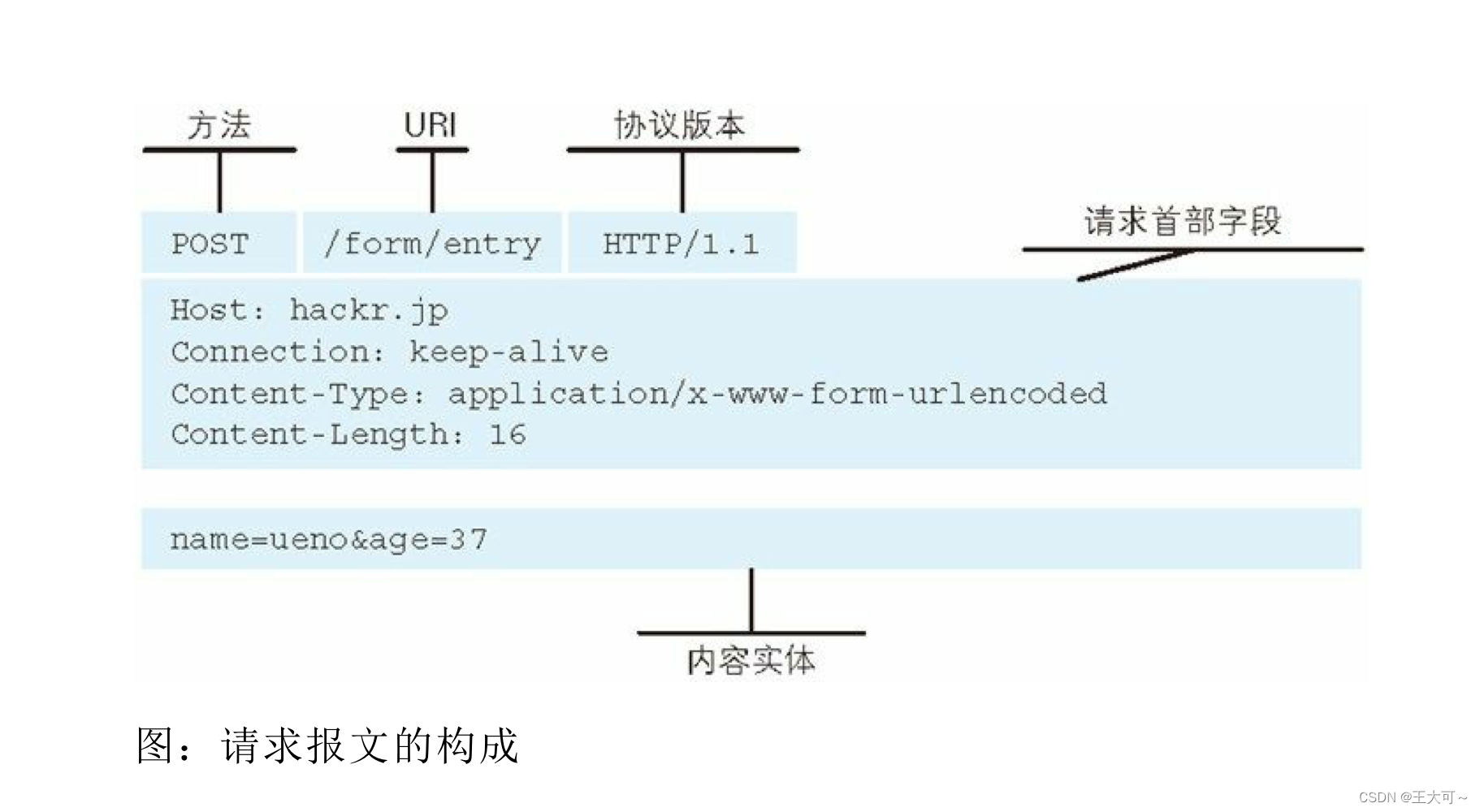
笔者引用《图解HTTP协议》书中的图示说明,其中请求方法、URL(URI)和协议版本构成的第一行内容是请求行(首行);接下来是请求头部(请求首部字段);然后空白部分是空行,用于分隔正文;最后剩下的内容便是正文(内容实体)。
对请求报文中内容进行逐一大致描述便是:请求行用于标识请求中的关键性描述信息;请求头部由多个键值对构成,用于对请求进行附加描述和对正文作以形容;空行用于分隔头部和正文;正文则是提交给服务器的数据内容。
解析来我们对请求报文的内容进行逐一细致解析,先对请求行中的内容进行仔细说明,首先是请求行中的请求方法:
| GET | 获取资源,用来请求访问已被URI识别的资源 |
| POST | 传输实体的主体,GET也能进行传输,但POST并不会获取响应的主体内容 |
| PUT | 传输文件,要求在请求报文中包含文件内容,然后保存在URI指定位置 |
| HEAD | 获得报文首部,同GET方法,但不返回报文主体 |
| DELETE | 删除文件,是和PUT方法相反的方法 |
| OPTIONS | 询问支持的方法,用于查询针对请求URI指定的资源支持的方法 |
| TRACE | 追踪路径,让Web服务器端将之前的请求通信返回给客户端 |
| CONNECT | 要求用隧道协议连接代理,用于和代理服务器实现用隧道协议进行TCP通信 |
其中最常使用的三种请求方法是:GET、POST和HEAD,还需注意GET和HEAD请求方法的区别。此外,附上HTTP1.0和HTTP1.1支持方法的差异:
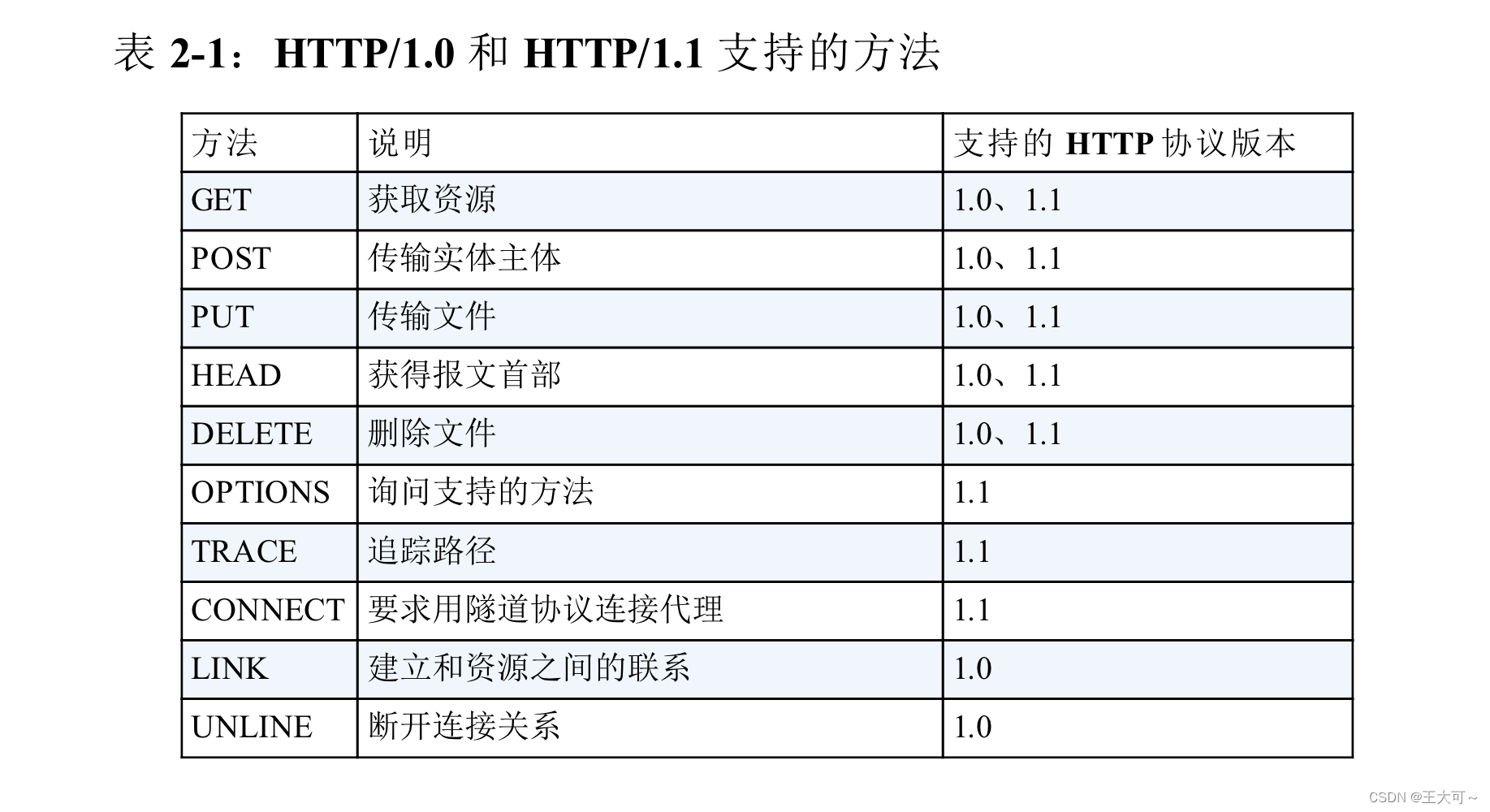 然后是URL(URI),URL是统一资源定位符,是一个具体的网站定位信息(网址),我们可以直接通过URL连接来访问到具体的连接;而这部分内容也可以是URI,URI也是用于定位互联网上的信息,和URL不同的是URI是一种标识,是一个相对的路径连接。(https是对http协议的加密)
然后是URL(URI),URL是统一资源定位符,是一个具体的网站定位信息(网址),我们可以直接通过URL连接来访问到具体的连接;而这部分内容也可以是URI,URI也是用于定位互联网上的信息,和URL不同的是URI是一种标识,是一个相对的路径连接。(https是对http协议的加密)
除此之外,如果不是访问特定资源而是对服务器本身发起请求时,我们可以使用一个 * 来代替请求URL(URI)。附上URL构成说明图片,同样出自于《图解HTTP》一书:

最后是协议版本,它所描述的是当前HTTP协议所使用的版本,不同的版本在功能支持力度上存在一些差距。具体的迭代过程,我们不做细究,有兴趣的伙伴可以阅读《图解HTTP》一书。
之后我们对请求头部内容进行解析,其中由一个个键值对构成,这是针对请求的一些附加描述,以及对请求正文的描述。需要注意的关键信息有:User-Agrant,Host,Referer……这些关键字来描述请求,还有:Content-Length和Content-Type者两者分别描述:正文长度和正文数据类型(决定对方如何解析数据)。
接下来是空行(/r/n)的解析,空行主要的作用也是前文我们所提到的:用于间隔HTTP头部和正文。实际上主要是用于实现HTTP解析时,先接收一个完整的HTTP头部,根据其中的Content-Length确定正文长度,然后根据长度取出指定大小的正文,则刚好能够获取一个完整的HTTP请求。
最后是正文,正文即是客户端提交给服务端的数据,其中的数据格式通过Content-Type来进行描述。
了解完HTTP请求格式(请求报文)后,我们来大概了解一些HTTP响应格式(响应报文):

首先是对于响应报文中的响应行(首行)中的内容,其中包括:协议版本、状态码和状态码描述。对于协议版本我们不做细究;然后是状态码,状态码主要用于明确告知客户端本次请求的处理结果,不同的状态码便代表不同的请求结果;最后是状态码的描述,状态码没有什么具体的功能意义,主要作用于告知程序员状态码的描述信息(文字)。
其次是对响应头部中的内容,需要注意的是Location关键字,其用来描述重定向,告知客户端上一次服务端所响应的连接;以及Connection关键字,用来描述当前所使用连接时短链接还是长连接。
然后是空行的作用同请求报文。最后正文即是响应给客户端的数据。
1.2.4Cookie
了解cookie之前,我们对HTTP的发展历程进行简单说明,也是为了回答我们在HTTP中为什么需要cookie。
在HTTP的初始版本中,每进行一次的HTTP通信就要断开一次TCP连接,这种连接方式也叫做短链接。这是因为在当时的通信情况中,数据都是一些容量很小的文本传输,所以即使每次连接都断开也不会产生问题。
但随着HTTP的普及,文本中包含大量图片的情况就多了起来。此时短链接的方式,在每次通信中会增加请求HTML页面的其他资源,扩大了通信量的开销。所以在HTTP1.1的一部分的HTTP1.0中提出了持久连接(长连接)。
这样的连接方式也叫做:HTTP keep-alive(HTTP connection reuse)方法。如此,在客户端和服务端通信中,只要其中任一端没有明确提出断开连接之前,则会一直保持TCP连接。在HTTP1.1中所有的连接默认都是持久连接,但在HTTP1.0中并未对其进行标准化。
持久化连接使得多数请求以管线化方式发送数据成为可能,在此之前发送请求后需要等待响应请求之后,才可以发送下一个请求。这样一问一答的方式,并不利于效率的提高。所以管线化技术实现后,我们不用等待也可以直接发送下一个请求。如此便可以做到通信并发多个请求,而不需要一个接一个的等待响应。
但仅对连接的优化使得通信效率提高并不能满足我们对通信的期待,因为HTTP是无状态协议,它并不会对之前发生的请求和响应状态进行存储和管理,这意味着我们无法根据之前的请求来对本次请求进行处理,我们无法将上下的响应内容相互联系。
当我们访问需要登录的Web页面时,由于它本身并不对登录状态进行管理(记录已登录的状态)。所以在每次跳转和刷新页面的时候,我们都需要重新在请求报文中添加登录信息。
从一方面来说,身为无状态协议的HTTP协议,由于不需要保存状态的原因,可以很有效的减少CPU及内存资源的消耗;但从另一方面来说,不保存状态并不列于我们对于一些场景的使用。
于是我们引入了Cookie技术(信息缓存机制),通过在请求报文和响应报文中写入Cookie信息来控制客户端的状态。Cookie根据响应报文中Set-Cookie的首部字段信息来通知客户端保存Cookie,当下一次客户端继续向服务端发送请求时,客户端会自动在请求报文中加入Cookie值再发送。
服务端会检查客户端发送过来的Cookie,通过其中内容识别出是那一个客户端发送的连接请求,然后对比服务器上的记录,最终得到之前的状态信息。
Cookie技术很好的解决的我们在多次通信中不断维护客户端的状态,但是这并不安全,当我们的通信被劫持之后,其中的敏感信息很容易被获取。所以我们并不能将敏感信息直接以Cookie的方式进行传输。
我们引入session会话机制,在客户端和服务端之间的通信建立一个会话,将会话的重要内容保存起来,会话内容将保存在服务器之中,接下来我们只需要通过Cookie传输session_id即可访问对应信息。如此便很好的避免了敏感信息的传输,提高了传输的安全性。
不过尽管如此仍存在一些安全隐患:Cookie篡改,于是引入token来解决。
1.3HTTPS协议
在了解HTTP协议之后,我们可以来讲述以下HTTPS协议。通俗而言,HTTPS协议实际上就是加密之后的HTTP协议。
因为HTTP协议在传输过程中容易被劫持,所以我们引入HTTPS协议对其进行加密,对于加密我们采取两种方式:身份加密和加密传输。
身份加密:我们采用CA认证,即电子认证服务。是通信双方到第三方权威机构,办理一份CA证书,当后面连接建立后,会将证书先发送给对方,对方对证书解析成功之后,双方才会进行正常的通信。
传输加密是对通信双方传输的数据进行加密。对于不同的加密方式我们存在不同的加密算法,通向双方需要对密钥(算法)进行协商,确定加密和解密的密钥。
我们将数据加密和解密使用相同密钥的传输加密称作对称加密;将数据加密和解密使用不同密钥的传输加密称作非对称加密。
对称加密:在传输过程中密钥容易被劫持,导致加密形同虚设,通信不安全;但是由于加解密采用密钥相同,其传输效率较高。
非对称加密:传输过程中我们使用相关算法生成一对密钥:公钥和私钥。在传输过程中,通信双发分别向对方发送自己的加密算法(公钥),并保留自己加密算法的解密密钥(私钥)。如此在通信过程中,客户端和服务端各自使用接收到的对方加密算法(公钥)来对传输的数据进行加密,通信双方再通过自己保留的解密算法(私钥)对数据进行解密,即可获得数据的原本内容。
非对称解密对传输数据的处理方式保证了数据传输的安全性,因为即使传输数据被劫持,对方知晓公钥也无法对数据解密;但是由于加解密算法的不同会导致传输更花费时间,效率较低。
为集合两种传输加密的优势,我们引入了混合加密的设计,来对对称加密和非对称加密都进行使用。其原理是:我们首先使用对称加密来快速对数据进行加密,数据将被处理为密文;然后我们将对称加密后的密文,当作非对称加密传输中的数据来进行处理即可。
因为对称加密对数据加密之后得到的密文长度比原数据长度更加简短,所以此时再采用非对称加密进行传输的话,便可以很好的避免非对称加密处理较长数据的解加密时间过长问题。
