自带浏览器建设银行网站打不开东莞网站建设营销网站
一、线程和进程对应的问题
**1.进程:**CPU密集型也叫计算密集型,指的是系统的硬盘、内存性能相对CPU要好很多,此时,系统运作大部分的状况是CPU Loading 100%,CPU要读/写I/O(硬盘/内存),I/O在很短的时间就可以完成,而CPU还有许多运算要处理,CPU Loading很高。
**2.线程:**IO密集型指的是系统的CPU性能相对硬盘、内存要好很多,此时,系统运作,大部分的状况是CPU在等I/O (硬盘/内存) 的读/写操作,此时CPU Loading并不高。
二、进程
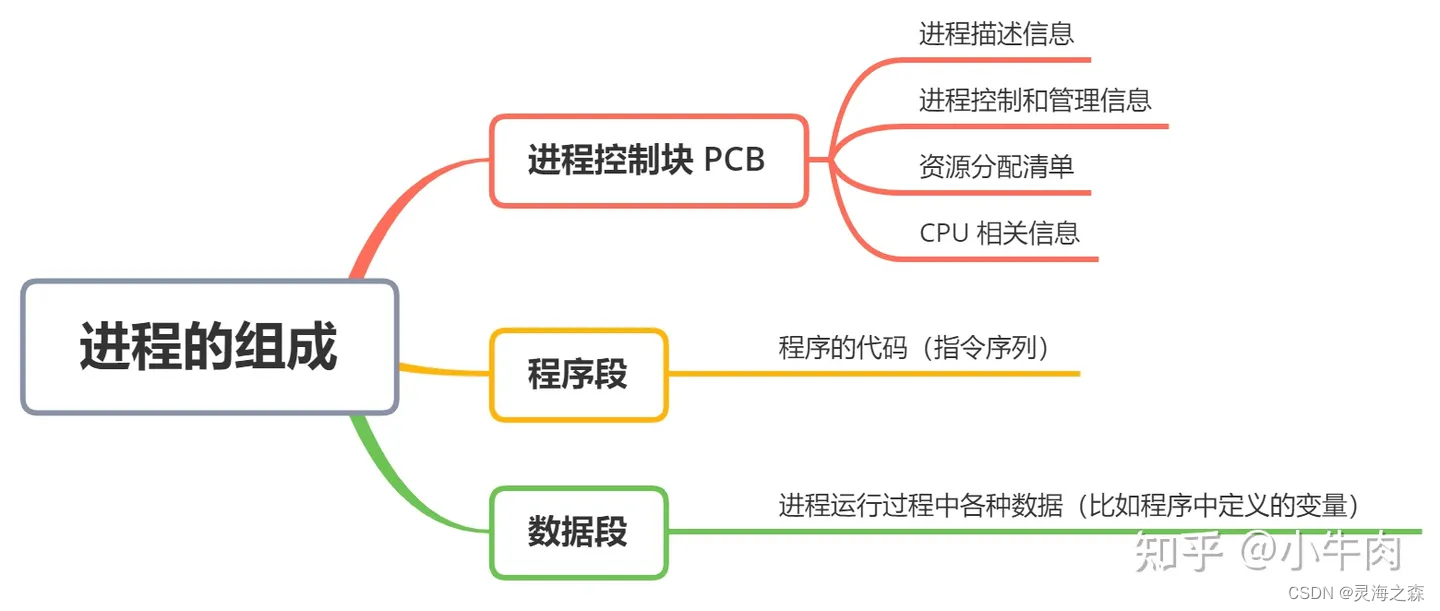
定义:进程是程序在某个数据集合上的一次运行活动,也是操作系统进行资源分配和保护的基本单位。
每个进程都有独立的代码和数据空间(进程上下文),进程间的切换会有较大的开销,一个进程包含1–n个线程。(进程是资源分配的最小单位)
CPython解释器本身就不是线程安全的,因此有全局解释器锁(GIL),一次只允许使用一个线程执行Python字节码。因此,一个Python进程通常不能同时使用多个CPU核心。
Python中的多进程实现:
futures.ProcessPoolExecutor类。现在流行multiprocessing模块。
import multiprocessing# 定义一个函数,用于在多个进程中执行任务
def worker_function(index):print(f"Worker {index} started")result = index * 2print(f"Worker {index} result: {result}")print(f"Worker {index} finished")if __name__ == "__main__":# 创建一个进程池,可以指定要创建的进程数(这里为3)num_processes = 3pool = multiprocessing.Pool(processes=num_processes)# 使用进程池执行任务# 这里将任务分配给三个进程并行执行pool.map(worker_function, range(num_processes))# 关闭进程池,等待所有进程完成pool.close()pool.join()print("All workers have finished")还有一种更简单的,使用
https://zhuanlan.zhihu.com/p/509084322
三、线程
进程中的一个执行任务(控制单元),负责当前进程中程序的执行。一个进程至少有一个线程,一个进程可以运行多个线程,多个线程可共享数据。
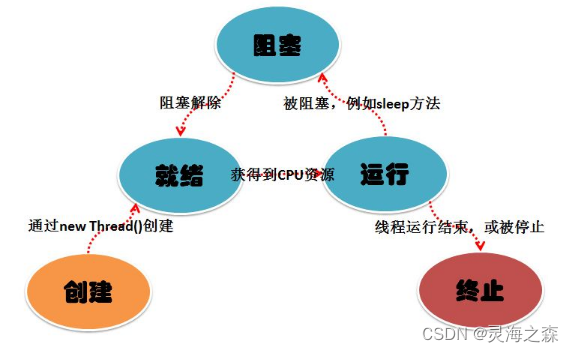
线程和进程都具有一砂锅五个状态。
Python中的实现:
import threading# 定义一个函数,用于在线程中执行任务
def worker_function(thread_id):print(f"Thread {thread_id} started")# 在这里可以执行一些任务print(f"Thread {thread_id} finished")if __name__ == "__main__":# 创建多个线程num_threads = 3threads = []for i in range(num_threads):thread = threading.Thread(target=worker_function, args=(i,))threads.append(thread)# 启动所有线程for thread in threads:thread.start()# 等待所有线程完成for thread in threads:thread.join()print("All threads have finished")四、二者的区别
多进程和多线程都是用于并发编程的技术,但它们有一些共性和区别:
共性:
-
并发性: 无论是多进程还是多线程,它们都允许在程序中执行多个任务,并在不同的执行上下文中交替执行这些任务,从而实现并发性。
-
共享资源: 多进程和多线程都可以访问共享的内存资源,这允许多个任务之间进行数据交换和共享数据。
-
并行执行: 在多核或多 CPU 的系统上,多进程和多线程都可以实现真正的并行执行,从而提高程序的性能。
区别:
-
独立性:
- 多进程:每个进程都有独立的内存空间和 Python 解释器,它们之间彼此独立,因此一个进程的错误通常不会影响其他进程。
- 多线程:所有线程共享同一进程的内存空间,它们之间共享全局变量和数据。因此,一个线程的错误可能会影响其他线程和整个进程。
-
创建和销毁:
- 多进程:创建和销毁进程通常比较慢,并且需要更多的系统资源,因为每个进程都有独立的内存空间。
- 多线程:创建和销毁线程通常更快,因为它们共享进程的内存空间,但线程之间的管理和同步可能更复杂。
-
并发性和并行性:
- 多进程:可以在多个 CPU 上并行执行,因此适用于 CPU 密集型任务。然而,多进程之间的通信开销相对较高。
- 多线程:在单个 CPU 上的并发性较强,适用于 I/O 密集型任务,但由于 GIL 的存在,多线程不能实现真正的多核并行。
-
同步和锁:
- 多进程:通常需要使用进程间通信(Inter-Process Communication,IPC)机制来实现进程之间的协作,例如管道、队列和共享内存。
- 多线程:线程之间可以更容易地共享数据,但需要使用锁(例如互斥锁)来确保线程安全。
-
资源开销:
- 多进程:通常比多线程消耗更多的内存和系统资源。
- 多线程:相对较轻量,消耗的资源较少。
