做网站的框架模版wordpress中文路径
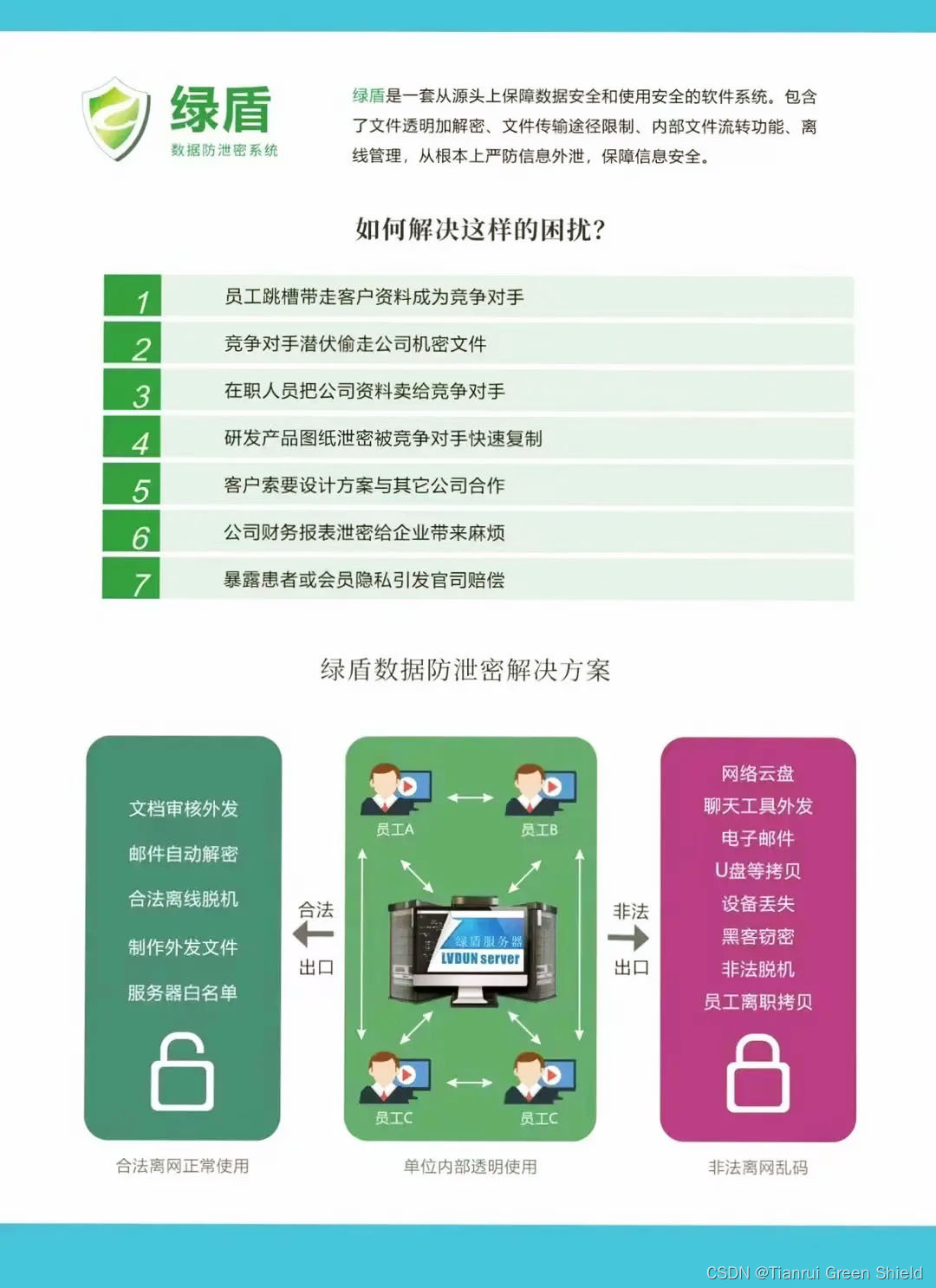
「天锐绿盾」是一种公司文件加密系统,旨在保护公司内网数据安全,防止信息泄露。该系统由硬件和软件组成,其中包括服务端程序、控制台程序和终端程序。

PC访问地址:
isite.baidu.com/site/wjz012xr/2eae091d-1b97-4276-90bc-6757c5dfedee
服务端程序需要运行在不关机的服务器电脑上,用于管理密钥及各种策略,存储终端的文件审批记录、文件解密记录等,并处理来自于客户端的各项验证,避免客户端可以随意安装和使用。服务端程序支持扩容,实现海量数据存储。
控制台程序运行在管理员电脑上,是系统的管理配置界面,通过网络与系统管理中心连接,对系统管理中心进行在线配置和管理。
终端程序则安装在员工电脑上,对电子文档进行实时动态保护,全程跟踪操作,控制各种可能造成泄密的途径。
「天锐绿盾」的重要功能还包括文件加密和加密软件部署,以及上网行为管理和文档加密管理。该系统已广泛应用于各行业的内网数据安全、网络准入控制及文档加密管理、数据防泄露等数据安全领域。
试用下载链接
www.drhchina.com——【德人合科技】提供软件系统及技术支持
#公司电脑文件加密系统#
