用手机能创建网站吗seo网址查询
机器翻译就是将一种语言翻译成另外一种语言,输入和输出的长度都是不定长的,所以这里会主要介绍两种应用,编码器-解码器以及注意力机制。
编码器是用来分析输入序列,解码器用来生成输出序列。其中在训练时,我们会使用一些特殊符号来表示,<bos>表示序列开始(beginning of sequence),<eos>表示序列的终止(end of sequence),<unk>表示未知符,以及<pad>用于补充句子长度的填充符号。
编码器的作用是将一个不定长的输入序列变换成一个定长的背景变量c,并在该背景变量中编码输入序列信息。编码器可以使用循环神经网络,对于循环神经网络的描述可以查阅前期的两篇文章:
循环神经网络(RNN)之门控循环单元(GRU)
循环神经网络(RNN)之长短期记忆(LSTM)
解码器输出的条件概率是基于之前的输出序列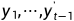 和背景变量c,即
和背景变量c,即
根据最大似然估计,我们可以最大化输出序列基于输入序列的条件概率:
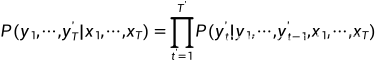
这里的 的输入序列的编码就是背景变量c,所以可以简化成:
的输入序列的编码就是背景变量c,所以可以简化成:
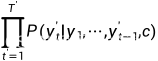
然后我们就可以得到该输出序列的损失:
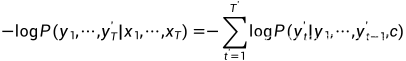
在模型训练中,所有输出序列损失的均值通常作为需要最小化的损失函数。在训练中我们也可以将标签序列(训练集的真实输出序列)在上一个时间步的标签作为解码器在当前时间步的输入,这叫做强制教学(teacher forcing)。
整理数据集
这里的数据集我们使用一个很小的法语-英语的句子对,名称是fr-en-small.txt的一个文本文档,里面是20条法语与英语的句子对,法语和英语之间使用制表符来隔开。内容如下(显示好像没有隔开了,这个自己使用Tab键隔开):
elle est vieille .she is old .
elle est tranquille .she is quiet .
elle a tort .she is wrong .
elle est canadienne .she is canadian .
elle est japonaise .she is japanese .
ils sont russes .they are russian .
ils se disputent .they are arguing .
ils regardent .they are watching .
ils sont acteurs .they are actors .
elles sont crevees .they are exhausted .
il est mon genre !he is my type !
il a des ennuis .he is in trouble .
c est mon frere .he is my brother .
c est mon oncle .he is my uncle .
il a environ mon age .he is about my age .
elles sont toutes deux bonnes .they are both good .
elle est bonne nageuse .she is a good swimmer .
c est une personne adorable .he is a lovable person .
il fait du velo .he is riding a bicycle .
ils sont de grands amis .they are great friends .
然后我们对这个数据集进行一些必要的整理,为上述的法语词和英语词分别创建词典。法语词的索引和英语词的索引相互独立。
import collections
import io
import math
from mxnet import autograd,gluon,init,nd
from mxnet.contrib import text
from mxnet.gluon import data as gdata,loss as gloss,nn,rnnPAD,BOS,EOS='<pad>','<bos>','<eos>'def process_one_seq(seq_tokens,all_tokens,all_seqs,max_seq_len):'''将一个序列中的所有词记录在all_tokens中'''all_tokens.extend(seq_tokens)#序列后面添加PAD直到序列长度变为max_seq_lenseq_tokens+=[EOS]+[PAD]*(max_seq_len - len(seq_tokens)-1)all_seqs.append(seq_tokens)def build_data(all_tokens,all_seqs):'''将上面的词构造词典,并将所有序列中的词变换为词索引后构造NDArray实例'''vocab=text.vocab.Vocabulary(collections.Counter(all_tokens),reserved_tokens=[PAD,BOS,EOS])indices=[vocab.to_indices(seq) for seq in all_seqs]return vocab,nd.array(indices)def read_data(max_seq_len):in_tokens,out_tokens,in_seqs,out_seqs=[],[],[],[]with io.open('fr-en-small.txt') as f:lines=f.readlines()for line in lines:in_seq,out_seq=line.rstrip().split('\t')in_seq_tokens,out_seq_tokens=in_seq.split(' '),out_seq.split(' ')if max(len(in_seq_tokens),len(out_seq_tokens)) > max_seq_len-1:continueprocess_one_seq(in_seq_tokens,in_tokens,in_seqs,max_seq_len)process_one_seq(out_seq_tokens,out_tokens,out_seqs,max_seq_len)in_vocab,in_data=build_data(in_tokens,in_seqs)out_vocab,out_data=build_data(out_tokens,out_seqs)return in_vocab,out_vocab,gdata.ArrayDataset(in_data,out_data)max_seq_len=7
in_vocab,out_vocab,dataset=read_data(max_seq_len)
print(in_vocab.token_to_idx)
'''
{'<unk>': 0, '<pad>': 1, '<bos>': 2, '<eos>': 3, '.': 4, 'est': 5, 'elle': 6, 'ils': 7, 'sont': 8, 'il': 9, 'mon': 10, 'a': 11, 'c': 12, 'elles': 13, '!': 14, 'acteurs': 15, 'adorable': 16, 'age': 17, 'amis': 18, 'bonne': 19, 'bonnes': 20, 'canadienne': 21, 'crevees': 22, 'de': 23, 'des': 24, 'deux': 25, 'disputent': 26, 'du': 27, 'ennuis': 28, 'environ': 29, 'fait': 30, 'frere': 31, 'genre': 32, 'grands': 33, 'japonaise': 34, 'nageuse': 35, 'oncle': 36, 'personne': 37, 'regardent': 38, 'russes': 39, 'se': 40, 'tort': 41, 'toutes': 42, 'tranquille': 43, 'une': 44, 'velo': 45, 'vieille': 46}
'''print(out_vocab.idx_to_token)
'''
{'<unk>': 0, '<pad>': 1, '<bos>': 2, '<eos>': 3, '.': 4, 'is': 5, 'are': 6, 'he': 7, 'they': 8, 'she': 9, 'my': 10, 'a': 11, 'good': 12, '!': 13, 'about': 14, 'actors': 15, 'age': 16, 'arguing': 17, 'bicycle': 18, 'both': 19, 'brother': 20, 'canadian': 21, 'exhausted': 22, 'friends': 23, 'great': 24, 'in': 25, 'japanese': 26, 'lovable': 27, 'old': 28, 'person': 29, 'quiet': 30, 'riding': 31, 'russian': 32, 'swimmer': 33, 'trouble': 34, 'type': 35, 'uncle': 36, 'watching': 37, 'wrong': 38}
'''
print(out_vocab.unknown_token)#<unk>
print(out_vocab.reserved_tokens)#['<pad>', '<bos>', '<eos>']
print(out_vocab.token_to_idx['arguing'],out_vocab.idx_to_token[17])#17 arguingprint(dataset[0])
'''
(
[ 6. 5. 46. 4. 3. 1. 1.]
<NDArray 7 @cpu(0)>,
[ 9. 5. 28. 4. 3. 1. 1.]
<NDArray 7 @cpu(0)>)
'''读取的数据集,我们查看了输入和输出的词典的一些属性,熟悉构建的词典里面的词与索引,也打印第一个样本看下,内容是法语和英语的词索引序列,长度为7,数据集整理好之后,我们接下来就是使用含有注意力机制的编码器-解码器来简单的做个机器翻译。
这里简短介绍下注意力机制,我们回头选一个法语-英语句子对示例来说明下,比如法语:“ils regardent .they are watching .”法语ils regardent .翻译成英语they are watching .我们发现其实英语they are只需关注法语中的ils,watching关注regardent,.直接映射即可。这个例子表明解码器在每一时间步对输入序列中不同时间步的表征或编码信息分配不同的注意力一样,这种机制就叫做注意力机制。
那么这里可以了解到,注意力机制通过对编码器所有时间步的隐藏状态做加权平均来得到背景变量c,解码器在每一时间步调整这些权重,即注意力权重,从而能够在不同时间步分别关注输入序列中的不同部分并编码进相应时间步的背景变量。本质上来讲就是,注意力机制能够为表征中较有价值的部分分配较多的计算资源。除了在自然语言处理NLP中应用,还广泛使用到图像分类,自动图像描述和语音识别等等。目前很火爆的ChatGPT是基于Transformer,而这个变换器模型的设计就是依靠注意力机制来编码输入序列并解码出输出序列的。
编码器
我们通过对输入语言的词索引做词嵌入得到特征(或叫词的表征),然后输入到一个多层门控循环单元中(GRU),在前面文章有介绍过,Gluon的rnn.GRU实例在前向计算后也会返回输出和最终时间步的多层隐藏状态。其中的输出指的是最后一层的隐藏层在各个时间步的隐藏状态,并不涉及输出层的计算,注意力机制将这些输出作为键项和值项。
class Encoder(nn.Block):def __init__(self, vocab_size,embed_size,num_hiddens,num_layers,drop_prob=0,**kwargs):super(Encoder,self).__init__(**kwargs)#词嵌入self.embedding=nn.Embedding(vocab_size,embed_size)#对输入序列应用多层门控循环单元(GRU) RNNself.rnn=rnn.GRU(num_hiddens,num_layers,dropout=drop_prob)def forward(self, inputs,state):#输入的形状是(批量大小,时间步数),所以需要交换为(时间步数,批量大小)embedding=self.embedding(inputs).swapaxes(0,1)return self.rnn(embedding,state)def begin_state(self,*args,**kwargs):return self.rnn.begin_state(*args,**kwargs)来测试下,使用一个批量大小为4,时间步数为7的小批量输入。其中门控循环单元的隐藏单元个数为16,隐藏层数设置为2。
编码器对该输入执行前向计算后返回的输出形状为(时间步数,批量大小,隐藏单元个数)
门控循环单元的多层隐藏状态的形状为(隐藏层个数,批量大小,隐藏单元个数),这里对门控循环单元来说state列表只含一个元素,即隐藏状态;如果使用长短期记忆,state列表还包含一个叫记忆细胞的元素。
encoder=Encoder(vocab_size=10,embed_size=8,num_hiddens=16,num_layers=2)
encoder.initialize()
output,state=encoder(nd.zeros((4,7)),encoder.begin_state(batch_size=4))
print(output.shape)#(7, 4, 16) (时间步数,批量大小,隐藏单元个数)
#state是列表类型
print(state[0].shape)#(2, 4, 16) (隐藏层个数,批量大小,隐藏单元个数)注意力机制
注意力机制的输入包括查询项、键项和值项。设编码器和解码器的隐藏单元个数相同,这里的查询项为解码器在上一时间步的隐藏状态,形状为(批量大小,隐藏单元个数);键项和值项均为编码器在所有时间步的隐藏状态,形状为(时间步数,批量大小,隐藏单元个数)
注意力机制返回当前时间步的背景变量,形状为(批量大小,隐藏单元个数)
在此之前先看下Dense里面的flatten参数为True和False的区别
Dense实例会将除了第一维之外的维度都看做是仿射变换的特征维,将输入转成二维矩阵(样本维个数,特征维个数)
dense1=nn.Dense(2,flatten=True)
dense1.initialize()
print(dense1(nd.zeros((3,5,7))).shape)#(3,2)如果我们希望全连接层只对最后一维做仿射变换,其他维的形状保持不变的话,只需将flatten项设置为False即可。
dense2=nn.Dense(2,flatten=False)
dense2.initialize()
print(dense2(nd.zeros((3,5,7))).shape)#(3,5,2)接下来上注意力模型代码:
def attention_model(attention_size):model=nn.Sequential()model.add(nn.Dense(attention_size,activation='tanh',use_bias=False,flatten=False),nn.Dense(1,use_bias=False,flatten=False))return modeldef attention_forward(model,enc_states,dec_state):#解码器隐藏状态广播到跟编码器隐藏状态形状相同后进行连结dec_states=nd.broadcast_axis(dec_state.expand_dims(0),axis=0,size=enc_states.shape[0])enc_and_dec_states=nd.concat(enc_states,dec_states,dim=2)e=model(enc_and_dec_states)#形状为(时间步数,批量大小,1)alpha=nd.softmax(e,axis=0)#在时间步维度做softmax运算return (alpha * enc_states).sum(axis=0)#返回背景变量做个测试,编码器的批量大小为4,时间步为10,编码器和解码器的隐藏单元个数都为8。注意力机制返回一个小批量的背景向量,每个背景向量的长度等于编码器的隐藏单元个数,因此输出形状为(4,8)
seq_len,batch_size,num_hiddens=10,4,8
model=attention_model(10)
model.initialize()
enc_states=nd.zeros((seq_len,batch_size,num_hiddens))
dec_state=nd.zeros((batch_size,num_hiddens))
print(attention_forward(model,enc_states,dec_state).shape)#(4, 8)其中attention_forward前向计算函数中的指定维度的广播broadcast_axis方法,附加示例说明下:
x = nd.array([[[1],[2]]])#(1, 2, 1)
#第三个维度进行广播,大小为3
print(nd.broadcast_axis(x,axis=2, size=3))
'''
[[[1. 1. 1.][2. 2. 2.]]]
<NDArray 1x2x3 @cpu(0)>
'''#将第一个维度和第三个维度进行广播,大小分别为2和3
print(nd.broadcast_axis(x, axis=(0,2), size=(2,3)))
'''
[[[1. 1. 1.][2. 2. 2.]][[1. 1. 1.][2. 2. 2.]]]
<NDArray 2x2x3 @cpu(0)>
'''含注意力机制的解码器
编码器搞定之后,来看下解码器,在解码器的前向计算中,我们先通过上面的注意力机制计算得到当前时间步的背景向量。由于解码器的输入来自输出语言的词索引,我们将输入通过词嵌入层可以得到表征,然后和背景向量在特征维连结。
我们将连结后的结果与上一时间步的隐藏状态通过门控循环单元计算出当前时间步的输出和隐藏状态。最后,我们将输出通过全连接层变换为有关各个输出词的预测,形状为(批量大小,输出词典大小)
class Decoder(nn.Block):def __init__(self,vocab_size,embed_size,num_hiddens,num_layers,attention_size,drop_prob=0,**kwargs):super(Decoder,self).__init__(**kwargs)self.embedding=nn.Embedding(vocab_size,embed_size)self.attention=attention_model(attention_size)self.rnn=rnn.GRU(num_hiddens,num_layers,dropout=drop_prob)self.out=nn.Dense(vocab_size,flatten=False)def forward(self,cur_input,state,enc_states):#使用注意力机制计算背景向量#将编码器在最终时间步的隐藏状态作为解码器的初始隐藏状态c=attention_forward(self.attention,enc_states,state[0][-1])#将嵌入的输入和背景向量在特征维进行连结input_add_c=nd.concat(self.embedding(cur_input),c,dim=1)#为连结后的变量增加时间步维,时间步个数为1output,state=self.rnn(input_add_c.expand_dims(0),state)#移除时间步维,输出形状为(批量大小,输出词典大小)output=self.out(output).squeeze(axis=0)return output,statedef begin_state(self,enc_state):#将编码器最终时间步的隐藏状态作为解码器的初始隐藏状态return enc_state训练模型
计算损失函数,并训练模型:
def batch_loss(encoder,decoder,X,Y,loss):batch_size=X.shape[0]enc_state=encoder.begin_state(batch_size=batch_size)enc_outputs,enc_state=encoder(X,enc_state)dec_state=decoder.begin_state(enc_state)#初始化解码器的隐藏状态dec_input=nd.array([out_vocab.token_to_idx[BOS]] * batch_size)#解码器的最初时间步输入为<bos>mask,num_not_pad_tokens=nd.ones(shape=(batch_size,)),0#使用mask掩码变量来忽略掉标签为填充项的损失l=nd.array([0])for y in Y.T:dec_ouput,dec_state=decoder(dec_input,dec_state,enc_outputs)l=l+(mask*loss(dec_ouput,y)).sum()dec_input=y#使用强制教学num_not_pad_tokens+=mask.sum().asscalar()mask=mask*(y!=out_vocab.token_to_idx[EOS])return l/num_not_pad_tokens#同时迭代编码器和解码器的模型参数
def train(encoder,decoder,dataset,lr,batch_size,num_epochs):encoder.initialize(init.Xavier(),force_reinit=True)decoder.initialize(init.Xavier(),force_reinit=True)enc_trainer=gluon.Trainer(encoder.collect_params(),'adam',{'learning_rate':lr})dec_trainer=gluon.Trainer(decoder.collect_params(),'adam',{'learning_rate':lr})loss=gloss.SoftmaxCrossEntropyLoss()data_iter=gdata.DataLoader(dataset,batch_size,shuffle=True)for epoch in range(num_epochs):l_sum=0.0for X,Y in data_iter:with autograd.record():l=batch_loss(encoder,decoder,X,Y,loss)l.backward()enc_trainer.step(1)dec_trainer.step(1)l_sum+=l.asscalar()if (epoch+1) % 10 == 0:print("epoch %d,loss %.4f" % (epoch+1,l_sum/len(data_iter)))embed_size,num_hiddens,num_layers=64,64,2
attention_size,drop_prob,lr,batch_size,num_epochs=10,0.5,0.01,2,50
encoder=Encoder(len(in_vocab),embed_size,num_hiddens,num_layers,drop_prob)
decoder=Decoder(len(out_vocab),embed_size,num_hiddens,num_layers,attention_size,drop_prob)
train(encoder,decoder,dataset,lr,batch_size,num_epochs)'''
epoch 10,loss 0.5872
epoch 20,loss 0.2703
epoch 30,loss 0.1843
epoch 40,loss 0.0730
epoch 50,loss 0.0354
'''机器翻译
损失函数写好了之后,我们试着来看下翻译的效果如何?
def translate(encoder,decoder,input_seq,max_seq_len):in_tokens=input_seq.split(' ')in_tokens+=[EOS]+[PAD]*(max_seq_len-len(in_tokens)-1)enc_input=nd.array([in_vocab.to_indices(in_tokens)])enc_state=encoder.begin_state(batch_size=1)enc_output,enc_state=encoder(enc_input,enc_state)dec_input=nd.array([out_vocab.token_to_idx[BOS]])dec_state=decoder.begin_state(enc_state)output_tokens=[]for _ in range(max_seq_len):dec_output,dec_state=decoder(dec_input,dec_state,enc_output)pred=dec_output.argmax(axis=1)pred_token=out_vocab.idx_to_token[int(pred.asscalar())]if pred_token==EOS:breakelse:output_tokens.append(pred_token)dec_input=predreturn output_tokensprint(translate(encoder,decoder,'ils regardent .',max_seq_len))#['they', 'are', 'watching', '.']
print(translate(encoder,decoder,'c est une personne adorable .',max_seq_len))#['he', 'is', 'a', 'lovable', 'person', '.']OK,翻译的效果还是很好,完美呈现。
评价翻译结果
当然上面的翻译是在训练数据集里面的,如果不在训练集里面的话,泛化能力如何呢?比如:print(translate(encoder,decoder,'ils sont canadiens .',max_seq_len))#['they', 'are', 'russian', '.']这个翻译出来的结果就错误了,正确翻译结果应该是They are Canadian.
所以我们最好是有个评估函数去评价它,一般使用BLEU(Bilingual Evaluation Understudy),直接上代码:
def bleu(pred_tokens,label_tokens,k):#预测的词与真实标签词的评估len_pred,len_label=len(pred_tokens),len(label_tokens)score=math.exp(min(0,1-len_label/len_pred))for n in range(1,k+1):num_matches,label_subs=0,collections.defaultdict(int)for i in range(len_label-n+1):label_subs[''.join(label_tokens[i:i+n])] += 1for i in range(len_pred-n+1):if label_subs[''.join(pred_tokens[i:i+n])]>0:num_matches+=1label_subs[''.join(pred_tokens[i:i+n])]-=1p=num_matches/(len_pred-n+1)score *= math.pow(p,math.pow(0.5,n))return scoredef score(input_seq,label_seq,k):pred_tokens=translate(encoder,decoder,input_seq,max_seq_len)label_tokens=label_seq.split(' ')print('BLEU %.3f,翻译结果:%s' % (bleu(pred_tokens,label_tokens,k),' '.join(pred_tokens)))score('ils regardent .','they are watching .',k=2)#BLEU 1.000,翻译结果:they are watching .
score('ils sont canadiens .','they are canadian .',k=2)#BLEU 0.658,翻译结果:they are russian .