模板网站建设代理商微信公众号排版编辑器
目的
本文主要是使用NetCore/Net8加上Redis来实现一个简单的秒杀功能,学习Redis的分布式锁功能。
准备工作
1.Visual Studio 2022开发工具
2.Redis集群(6个Redis实例,3主3从)或者单个Redis实例也可以。
实现思路
1.秒杀开始前,将商品的数量缓存到Redis中
2.使用Redis的分布式缓存锁,保证只有一个人能获取到锁,进而保证减库存的操作的原子性。
3.获取到Redis分布式锁后,开始后续的业务操作,减少库存。
实现代码
// See https://aka.ms/new-console-template for more information
using StackExchange.Redis;WriteLine("开始秒杀活动......");
WriteLine("请输入秒杀商品的ID,按回车键确认:", ConsoleColor.Blue);//ThreadPool.SetMinThreads(200, 200);var db = GetDataBase();string? productId = Console.ReadLine();
if (!string.IsNullOrWhiteSpace(productId))
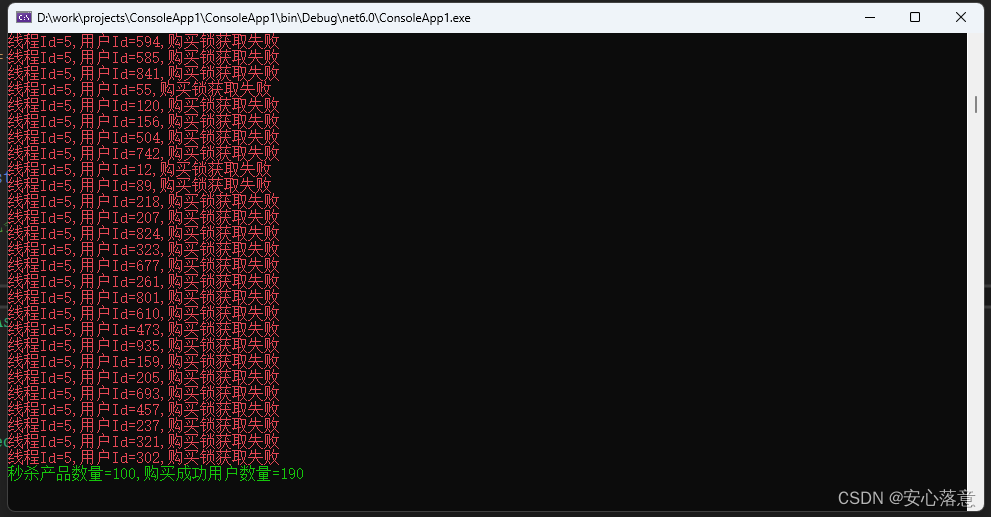
{int maxProductNumber = 100;//设置商品的最大库存数量await db.StringSetAsync($"ProductNumber:{productId}", maxProductNumber);//开始模拟购买List<Task> allTaskList = new List<Task>();for (int i = 0; i < 1000; i++){var task = BuyProduct(db, buyerId: i);allTaskList.Add(task);}await Task.WhenAll(allTaskList);int buySuccessNumber = Directory.GetFiles($"{AppContext.BaseDirectory}/buyer/").Length;WriteLine($"秒杀产品数量={maxProductNumber},购买成功用户数量={buySuccessNumber}", ConsoleColor.Green);Console.ReadLine();
}
else
{Console.WriteLine("输入商品ID为空,自动退出");
}IDatabase GetDataBase()
{ConnectionMultiplexer cm = ConnectionMultiplexer.Connect("127.0.0.1:6379,127.0.0.1:6380,127.0.0.1:6381,127.0.0.1:6382,127.0.0.1:6383,127.0.0.1:6384");return cm.GetDatabase();
}async Task BuyProduct(IDatabase db, int buyerId)
{int threadId = Environment.CurrentManagedThreadId;try{//首先获取当前库存,判断是否还可以购买var leftProductNumber = await GetProductCurrentNumberAsync(db, productId);if (leftProductNumber < 1){WriteLine($"线程Id={threadId},购买失败,用户Id:{buyerId},库存不足1,当前库存:{leftProductNumber}", ConsoleColor.Red);return;}string key = $"ProductId:{productId}";string lockValue = Guid.NewGuid().ToString();//锁的过期时间一定要比成功获取锁后操作业务所需的时间长,//否则会导致业务还没有操作完成(减库存)锁就释放了,导致后面的用户获取到锁,最终导致超卖的情况bool lockSuccess = await GetLockAsync(db, key, lockValue, TimeSpan.FromSeconds(5));if (!lockSuccess){WriteLine($"线程Id={threadId},用户Id={buyerId},购买锁获取失败", ConsoleColor.Red);return;}try{//再次获取当前库存,判断是否还可以购买leftProductNumber = await GetProductCurrentNumberAsync(db, productId);if (leftProductNumber < 1){WriteLine($"线程Id={threadId},购买失败:{lockValue},用户Id:{buyerId},库存不足2,当前库存:{leftProductNumber}", ConsoleColor.Red);return;}//扣减库存await db.StringDecrementAsync($"ProductNumber:{productId}");WriteLine($"线程Id={threadId},购买成功:{lockValue},用户Id:{buyerId}", ConsoleColor.Green);var dirPath = $"{AppContext.BaseDirectory}/buyer";if (!Directory.Exists(dirPath)){Directory.CreateDirectory(dirPath);}await File.WriteAllTextAsync($"{dirPath}/buy-success-{buyerId}.txt", $"锁Id={lockValue},用户Id={buyerId},产品Id={productId},剩余产品数量={leftProductNumber}");}finally{bool lockReleased = await db.LockReleaseAsync(key, lockValue);if (!lockReleased){WriteLine($"线程Id={threadId},用户Id={buyerId},锁释放失败:{lockValue}", ConsoleColor.Yellow);}}}catch(Exception ex){WriteLine($"线程Id={threadId},用户Id={buyerId},购买失败:{ex}", ConsoleColor.Red);}
}async Task<bool> GetLockAsync(IDatabase db, string key, string lockValue, TimeSpan timeout)
{//每个用户有五次获取Redis分布式产品锁的机会,如果5次重试后,都没有获取到锁,则默认秒杀失败int i = 5;while (i > 0){bool lockSuccess = await db.LockTakeAsync(key, lockValue, timeout);if (lockSuccess){return true;}await Task.Delay(TimeSpan.FromMilliseconds(new Random(Guid.NewGuid().GetHashCode()).Next(100, 500)));i--;}return false;
}async Task<long> GetProductCurrentNumberAsync(IDatabase db, string productId)
{string? leftProductNumberString = await db.StringGetAsync($"ProductNumber:{productId}");_ = long.TryParse(leftProductNumberString, out long leftProductNumber);return leftProductNumber;
}static void WriteLine(string text, ConsoleColor colour = ConsoleColor.White)
{Console.ForegroundColor = colour;Console.WriteLine(text);
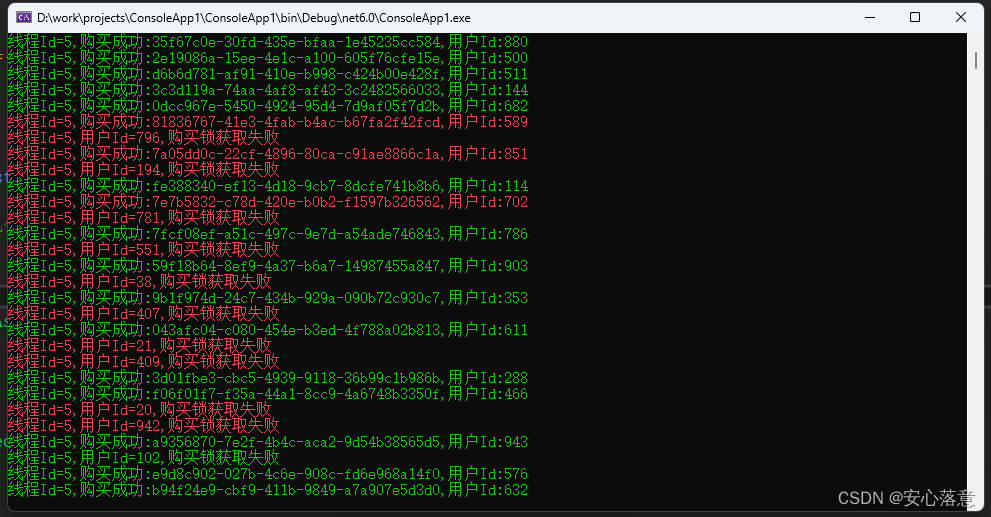
}运行效果