湛江市建设局官方网站树莓派架设wordpress
目录
- 一、RabbitMQ 集群原理
- 1、默认集群原理
- 2、镜像集群原理
- 3、负载均衡方案
- 二、RabbitMQ 高可用集群搭建
- 1、RabbitMQ 集群搭建
- 2、配置镜像队列
- 3、HAProxy 环境搭建
- 4、Keepalived 环境搭建
一、RabbitMQ 集群简介
1、默认集群原理
3-1、RabbitMQ 集群简介
单台 RabbitMQ 服务器处理消息的能力是有瓶颈的,而且可靠性还无法保证,所以需要通过集群来提高消息的吞吐量和提高数据可靠性。
由于 RabbitMQ 本身是基于 Erlang 编写,而 Erlang 语言天生具备分布式特性(通过同步 Erlang 集群各节点的 erlang.cookie 来实现)。因此,RabbitMQ 天然支持集群,并且还能通过水平扩展节点的方式提高吞吐量。
在一个多节点的 RabbitMQ 集群中,Exchange(交换器)的元数据(Metadata)信息在所有节点上都是一致的,而 Queue(存放消息的队列)的完整数据只会存在于创建它的那个节点上,其他节点只知道这个 Queue 的 Qetadata 信息和一个指向 Queue 的 owner node 的指针(起到消息转发作用)。
3-2、RabbitMQ 集群同步的元数据
RabbitMQ 集群会始终同步以下四种类型的内部元数据:
- Queue 元数据:队列名称和它的属性;
- Exchange 元数据:交换器名称、类型和属性;
- Binding 元数据:一张简单的表格展示了如何将消息路由到队列;
- VHost 元数据:为 VHost 内的队列、交换器和绑定提供命名空间和安全属性;
所以,当用户访问其中任何一个 RabbitMQ 节点时,通过 rabbitmqctl 查询到的 Queue/Exchange/Binding/VHost 等信息都是相同的。
3-3、为什么 RabbitMQ 集群只同步元数据?
- 第一,存储空间。如果每个集群节点都拥有所有 Queue 的完全数据,那么每个节点的存储空间会非常大,集群的消息积压能力会非常弱(无法通过集群节点的扩容提高消息积压能力);
- 第二,性能。消息的发布者需要将消息复制到每一个集群节点,对于消息持久化、网络和磁盘同步复制的开销都会明显增加。
3-4、RabbitMQ 集群发布/订阅消息的基本原理
集群原理图如下:
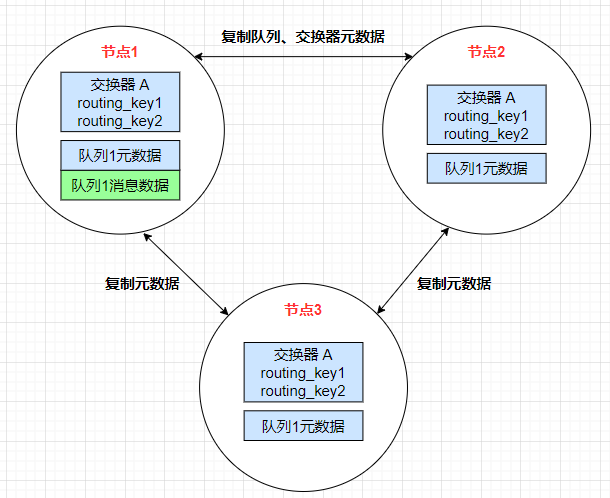
客户端消息收发有以下两种情况:
- 客户端直接连接队列所在的节点: 如果消息生产者或者消费者通过
amqp-client的客户端连接至节点 1 进行消息的发布或者订阅,那么此时的集群中的消息收发只与节点 1相关。 - 客户端连接的是非队列数据所在的节点: 如果消息生产者所连接的是节点 2 或者节点 3,此时,由于队列 1 的完整数据不在该两个节点上,所以在发送消息时这两个节点会根据节点上队列 1 的元数据将消息转发至节点1上,最终发送的消息还是会存储至节点 1 的队列 1 上(这两个节点主要起了一个路由转发作用)。同样,如果消息消费者所连接的节点在 2 或者 3,那这两个节点也会作为路由节点起到转发作用,将会从节点 1 的队列 1中 拉取消息进行消费。
3-5、集群节点类型
RabbitMQ 集群节点分为磁盘节点和内存节点两种类型:
- 磁盘节点: 将配置信息和元信息存储在磁盘上(单节点系统必须是磁盘节点,否则每次重启 RabbitMQ 之后所有的系统配置信息都会丢失)。
- 内存节点: 将配置信息和元信息存储在内存中,性能是优于磁盘节点的。
RabbitMQ 要求集群中至少有一个磁盘节点,当节点加入和离开集群时,必须通知磁盘节点(如果集群中唯一的磁盘节点崩溃了,则不能进行创建队列、创建交换器、创建绑定、添加用户、更改权限、添加和删除集群节点)。
总之如果唯一磁盘的磁盘节点崩溃,集群是可以保持运行的,但不能更改任何东西。因此建议在集群中设置两个磁盘节点,只要一个可以,就能正常操作。
2、镜像集群原理
2-1、镜像集群简介
RabbitMQ 在普通集群模式下,可以提高消息的吞吐量,但不能保证队列的高可用。尽管交换机、绑定这些可以复制到集群里的任何一个节点,但是队列内容不会复制。虽然该模式解决一项目组节点压力,但队列节点宕机直接导致该队列无法应用,只能等待重启。
所以,要想在队列节点宕机或故障时也能正常使用,就要复制队列内容到集群里的每个节点,这些队列就是镜像队列,而镜像集群就是 RabbitMQ 集群的高可用部署方案(HA方案)。
RabbitMQ 镜像集群模式是在普通集群模式的基础上配置镜像队列模式来实现的,换句话说就差 RabbitMQ 镜像集群依赖于普通集群,所以,要搭建镜像集群就需要先搭建普通集群。镜像集群模式其实就是把需要的队列做成镜像队列,然后将镜像队列放在多个 RabbitMQ 节点当中。
2-2、镜像队列架构
普通队列的进程及其数据仅仅维持在单个节点上,所以当其所在的节点失效后就会导致对应的队列不可用。
引入镜像队列(Mirror Queue)的机制,可以将队列镜像到集群中的其他 Broker 节点之上,如果集群中的一个节点失效了,队列能够自动切换到镜像中的另一个节点上来保证服务的可用性。
每个镜像队列都包含一个主节点(master)和若干个从节点(slave),架构图如下:

我们以3个 Broker 节点为例,假如在节点1创建了队列1的 master 队列,则会在节点2和3中各镜像一个对应的 slave 队列,这些 master 队列节点和所有 slave 队列节点会形成一个循环链表结构。
由于 master 队列提供读写服务,而在 slave 上的操作都会路由到 master 上(slave 只做备份-主备切换),所以同一个队列的负载基本上会集中在一个节点上。为了尽可能地确保各节点的负载均衡,我们需要将队列的 master 节点均匀散落在集群中的各个 Broker 节点上,比如队列2的 master 放在节点2,而对应的 slave 则放在节点1和3上,以此类推。当然每个 master 队列消息请求的数量可能会有不同,无法保持绝对的负载均衡。
2-3、镜像队列的工作原理
消息的发布(除了 Basic.Publish 之外)与消费都是通过 master 队列完成。master 对消息进行处理的同时将消息的处理动作通过 GM 广播给所有的 slave 队列,slave 队列所在的节点的 GM 收到消息后,通过回调交由对应的镜像 slave 队列进行实际的处理。
而对于 Basic.Publish,消息会同时发送到 master 和所有 slave 上,如果此时 master 宕掉了,由于消息还发送到了 slave 上,这样当 slave 提升为 master 的时候消息也不会丢失。
GM(Guarenteed Multicast) 即可靠的组播通讯协议,该协议能够保证组播消息的原子性,即保证组中活着的节点要么都收到消息要么都收不到。
GM 的工作原理如下:
- GM 将所有的 Broker 节点形成一个循环链表,每个节点都会监控位于自己左右两边的节点,当有节点新增时,相邻的节点保证当前广播的消息会复制到新的节点上;当有节点失效时,相邻的节点会接管保证本次广播的消息会复制到所有的节点。
- 在 master 队列的节点和 slave 队列的节点上的 GM 形成一个 group(gm_group),group 的信息会记录在
mnesia中(不同的镜像队列形成不同的 group)。消息从 master节点对应的 GM 发出后,顺着链表依次传送到所有的节点,由于所有节点组成一个循环链表,master 队列所在的节点对应的 GM 最终会收到自己发送的消息,这个时候 master 就知道消息已经复制到所有的 slave 队列了。
镜像队列间的消息流转:
当消费者与 master 队列建立连接,消费者可以直接从 master 队列上获取信息,当消费者与 slave 队列建立连接呢?消费者是从 slave 队列直接获取数据的吗?当然不是的,消息的流转顺序如下所示:
- slave 队列先将消费者的请求转发给 master 队列;
- 然后再由 master 队列准备好数据返回给 slave 队列;
- 最后由 slave 队列将消息返回给消费者。
节点失效:
如果某个 slave 失效了,系统处理做些记录外几乎啥都不做。master 依旧是 master,客户端不需要采取任何行动,或者被通知slave失效。
如果 master 失效了,那么 slave 中的一个必须被选中为 master。被选中作为新的 master 的 slave 通常是最老的那个(基于slave加入cluster的时间排序),因为最老的 slave 与前任 master 之间的同步状态应该是最好的。需要注意的是,如果没有任何一个 slave 与 master 完全同步的话,那么旧 master 中未被同步的消息将会丢失。
新节点消息同步:
每当一个节点加入或者重新加入(例如从网络分区中恢复过来)镜像队列,该节点之前保存的队列内容会被清空。
将新节点加入已存在的镜像队列时,默认情况下 ha-sync-mode=manual,镜像队列中的消息不会主动同步到新节点,除非显式调用同步命令。当调用同步命令后,队列开始阻塞,无法对其进行操作,直到同步完毕。当 ha-sync-mode=automatic 时,新加入节点时会默认同步已知的镜像队列,但由于同步过程的限制,所以不建议在生产的消费队列中操作。
简单总结一下:
镜像队列的引入可以极大地提升 RabbitMQ 的可用性及可靠性,提供了数据冗余备份、避免单点故障的功能,一旦 master 队列不可用,最老的 slave 队列将被选举为新的 master 队列。
同时镜像队列也会带来明显的缺点:由于镜像队列需要为每一个节点都要同步所有的消息实体,所以会导致网络带宽压力很大。 而提供了数据的冗余备份,会导致存储压力变大,可能会出现IO瓶颈
3、负载均衡方案
本质上镜像队列只是有一个备份队列,所以不能作为负载均衡使用。也就是说对于一个三节点的集群,每个节点的负载可能都是不相同的。
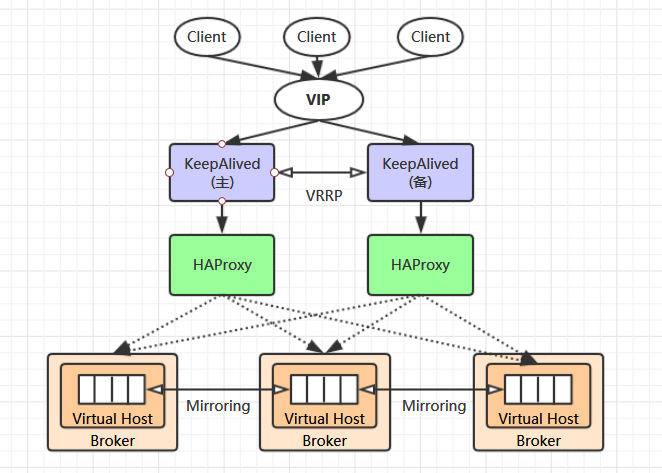
我们可以通过硬件负载均衡或者软件负载均衡的方式解决这个问题,这里我们选择使用软件 HAProxy 来进行负载均衡,当然也可以使用其他负载均衡中间件,如 LVS 等。HAProxy 同时支持四层和七层负载均衡,并基于单一进程的事件驱动模型,因此它可以支持非常高的井发连接数。
假如我们只采用一台 HAProxy ,那么它就存在明显的单点故障的问题,所以至少需要两台 HAProxy ,同时这两台 HAProxy 之间需要能够自动进行故障转移,常用的解决方案就是 KeepAlived 。KeepAlived 采用 VRRP (Virtual Router Redundancy Protocol,虚拟路由冗余协议)来解决单点失效的问题,它通常由一主一备两个节点组成,同一时间内只有主节点会提供对外服务,并同时提供一个虚拟的 IP 地址 (Virtual Internet Protocol Address ,简称 VIP) 。 如果主节点故障,那么备份节点会自动接管 VIP 并成为新的主节点 ,直到原有的主节点恢复。
最后,任何想要连接到 RabbitMQ 集群的客户端只需要连接到虚拟 IP,而不必关心集群是何种架构,示例如下:
ConnectionFactory factory = new ConnectionFactory();
// 假设虚拟ip为 192.168.0.100
factory.setHost("192.168.0.100");
整体架构图如下:
二、RabbitMQ 高可用集群搭建
1、RabbitMQ 集群搭建
首先需要搭建 RabbitMQ 集群。
