本地合肥网站建设网站建设公司需要什么
作者介绍:王海峰,数据库系统架构师,YashanDB SQL开发负责人,10年以上数据库内核技术开发经验。
Oracle兼容性是目前国产数据库的关键任务之一,其直接影响到商业迁移的成本和竞争力。
我们经常发现,部分国产数据库声称与 Oracle兼容性高达90%,但在实际迁移过程中,仍需要频繁地修改业务应用的代码。为何实现与Oracle高兼容度的数据库产品如此困难?其中一个重要原因是Oracle兼容性不仅是模仿,而是一个非常复杂和工程量庞大的逆向工程。其技术实现的复杂性以及多如牛毛的细节,足以让多数“年轻”的数据库团队望洋兴叹。
强可扩展性的自主SQL引擎
SQL的本质在于理解用户编写SQL语句的意图,将其转成高效执行计划,然后操作和管理数据库执行要求的算子,返回对应结果集。其过程需要实现编译、优化、执行3步曲。

图 1 SQL 3步曲
对于YashanDB的SQL引擎来说,为了快速实现Oracle兼容性,从架构实现上采取了有效的方法:通过对SQL语法、函数、数据类型、存储过程语法、高级包、优化规则、执行算子等各个维度进行抽象和归纳,在SQL引擎的各个功能阶段提供功能注册点。由于全链路的代码都是自主研发,我们可以在框架内通过扩展功能注册点来快速添加各种兼容性功能,对于部分涉及调整框架的需求,也能够确保整个架构的稳定性。
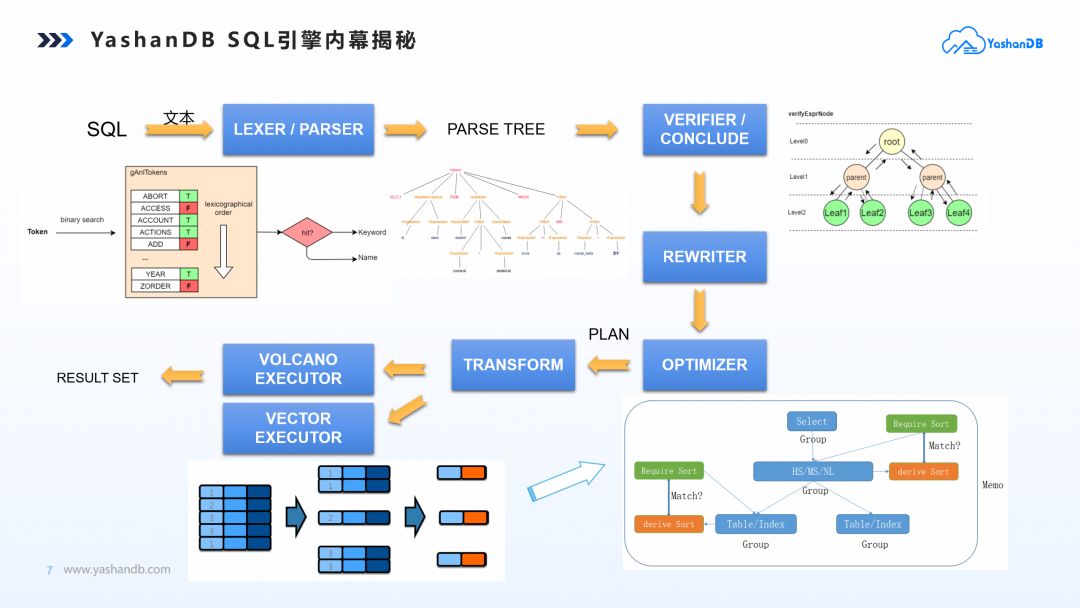
解析器(LAXER/PARSER):YashanDB全新实现了词法解析器和语法解释器,通过对注册关键字的定界,精准地生成符合查询语义的抽象语法树。语法树以高效的表达式符号作为基本组成单元,为后续环节提供输入。不同于其他数据库,YashanDB没有采用开源组件进行抽象语法树的编译,主要从语法支持的灵活度、语法编译生成语法树的高效性以及开发者开发和调试的易用性等角度考虑。
优化器(OPTIMIZER):YashanDB的SQL引擎为了达到极致性能,同时支持了行列两类算子分别满足低时延短事务和大数据查询场景的差异化需求。在优化器方面,我们面临着一个更具挑战性的任务:需要实现面向差异化代价模型的行列混合评估、行列统一的并行优化框架以及面向特定模型的动态优化规则。由于没有现成的道路可走,我们选择自主研发,为YashanDB打造一款适合高速查询优化的优化器。
高效的执行引擎(EXECUTOR):YashanDB同时涵盖了低时延段事务的TP场景和海量数据查询的AP场景,所以火山、向量化、并行化的执行引擎技术应运而生。
Oracle已经建立了一套成熟且卓越的技术体系,要想做到完全兼容,不仅需要投入大量的人力、物力和时间,还需要深入理解其内部运作原理和实现细节。以Oracle 19c为例,在SQL层主要功能罗列如下:
- 语法和常见功能函数;
- 结构化数据类型;
- JSON、XML等半结构化数据及功能;
- 查询加速提升,如OLAP、并行处理、结果集缓存等;
- 如UDT、高级包、存储过程、触发器等各种高级特性;
- 安全、加密和审计;
- 工具生态上大量的衍生工具和中间件等。
数据库是一个极其复杂的软件工程产品,不能简单地视为一个无需调整即可直接复用的通用组件。时至今日,SQL标准仍在不断发展,ISO/IEC 9075:2023等新标准不断涌现。对于国产数据库厂商而言,在Oracle兼容方面需保持务实的态度,将重点放在核心功能的实现上,对其保持高度的兼容性与稳定性。正是因为自主研发打造的SQL引擎,我们不仅能够在Oracle兼容性方面持续追求全面兼容的目标,更重要的是可以将我们的创新理论更好地融入到SQL架构中,将有界计算、向量化、多模等技术天然融合、持续演进。
YashanDB从设计之初,就定下Oracle全面兼容的目标。目前已从四个层面实现了高度的Oracle兼容性:
- 语法兼容层面:目前主流的DQL、DML、HINT语法、PL/SQL语法已全面兼容;
- 语义兼容层面:SQL语义保持一致,包含语法对应的语义实现、对象管理和事务处理等;
- 高级特性兼容层面:1)PL/SQL对象如存储过程、UDF、UDP、触发器、JOB等全面兼容;2)JSON、GIS等新型数据类型功能兼容,提供等价替换方案;3)安全、加密和审计全面兼容;4)查询加速提升能力同步构建;
- 生态兼容层面:提供AWR/RMAN/开发者工具等能力。
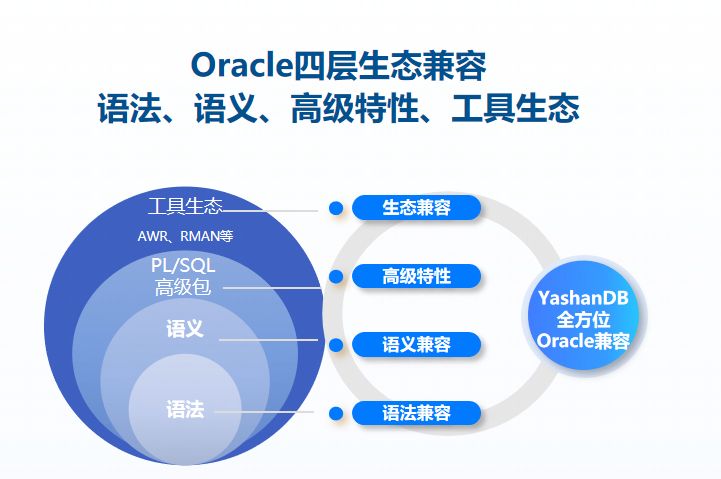 图3 Oracle四层生态兼容
图3 Oracle四层生态兼容 下面将以语法兼容层面的数据类型、SQL语法功能、部分高级特性角度,详细阐述YashanDB在Oracle兼容性上面临的挑战和应对的开发原则。
数据类型
数据类型兼容方面,YashanDB与Oracle高度兼容,其功能表现差异很小,主要包含数值类型组、字符串类型组、时间类型组和其他类型:
数值类型组:Oracle几乎所有数值类型均使用NUMBER来实现,为了应对这一挑战,YashanDB实现了一个极其高效的NUMBER类型,用户在Oracle数据库上定义的数值类型可以无缝迁移到YashanDB。此外,为了进一步提高存取和计算效率,YashanDB增加了各种C语言原生类型,如TINYINT、BIGINT、FLOAT、DOUBLE等,在表字段设计上可以提供更多灵活的选择,如果原生类型可以满足用户的表字段设计,那么建议调整为原生类型;
字符串类型组:精心打造CHAR、VARCHAR、NCHAR、NVARCHAR等各类字符串类型,追求细节层面的功能表现。在字符串类型规格、运算能力、隐式转换能力、空串表达以及字符集支持等各方面均做到易用、易理解、易维护的较高水准。YashanDB始终坚持既定的功能设计原则,以易于接受和理解的方式设计产品的功能表现。
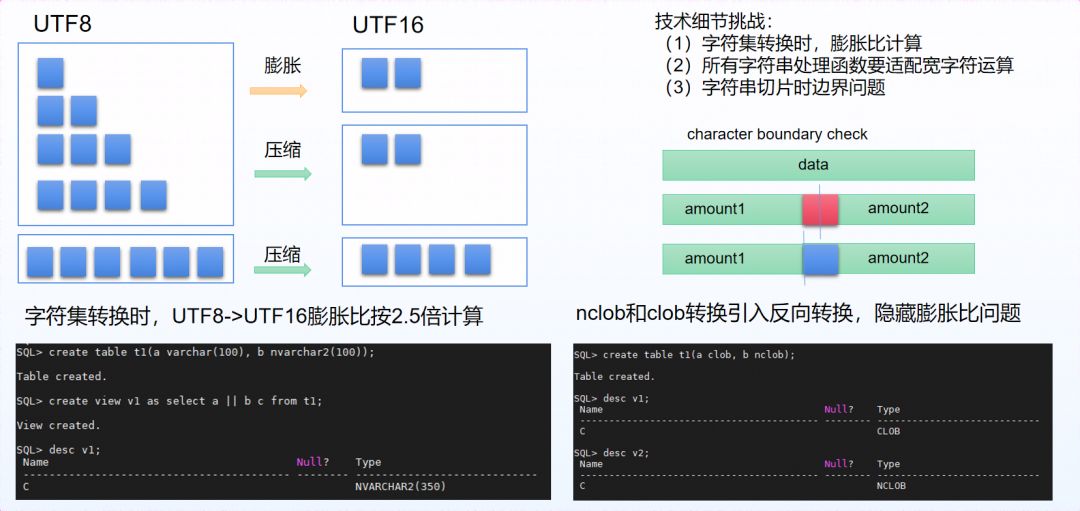
图 4 不同字符集的技术挑战
时间类型组:当前YashanDB提供了DATE、TIMESTAMP、YM-INTERVAL、DS-INTERVAL等类型用于满足迁移和设计要求。在该特性开发上,面临的技术挑战主要是时间类型的格式符处理非常灵活和不同场景下时间类型的优化选择;
二进制数据和大对象数据:随着信息系统的发展,对二进制数据和大对象数据的需求也日益增长,YashanDB在二进制类型、CLOB/BLOB/NCLOB等大对象类型做了大力的开发。在这些数据类型上,针对性地开发了查询加速结构、函数运算和空间管理等特性,以提升对象存取和运算效率。
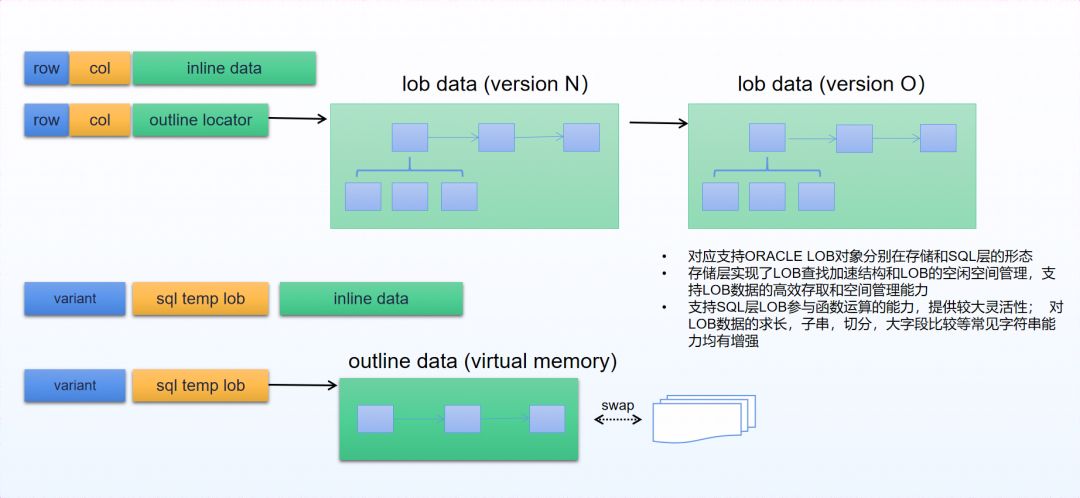 图 5 LOB类型的技术细节
图 5 LOB类型的技术细节 此外,在数据库预置的数据类型基础上,提供了UDT自定义类型便于用户灵活的指定和扩展。YashanDB的UDT可以用于PL/SQL语言中,也可以直接作为表的列字段类型形成嵌套表。
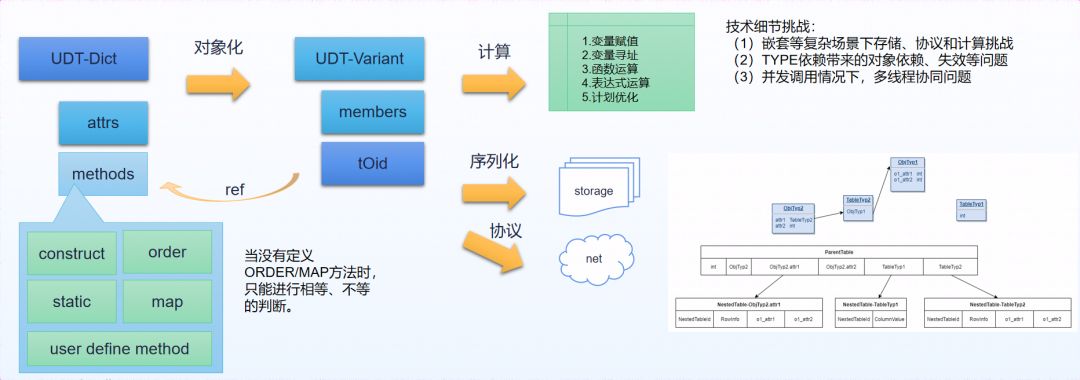 图 6 UDT类型的技术挑战
图 6 UDT类型的技术挑战 SQL语法能力和内置功能
SQL语法功能实现上, YashanDB的DML/DQL已经包括运算符、FILTER、内连接、外连接、半连接、反半连接、分组、聚合、排序、集合、层次查询、子查询等能力,用户在Oracle上实现的SQL语句,几乎可以不用调整直接在YashanDB上运行。 我们严格遵循语法语义要求,在语义获取上不断地比对Oracle、DB2、PostgreSQL、MySQL等数据库的功能表现,以确保生成严谨的、经得起推敲的产品。同时内部通过混沌测试工程,不断构造非法或者复杂的SQL语句进行测试。
高级特性
数据库的高级特性往往涉及到较高的技术挑战,如UDF(用户自定义函数)、JAVA UDF、C UDF、存储过程、高级包、UDT、触发器、JOB、DBLINK等。我们在借鉴Oracle已有实现能力基础上,追寻技术上的自主独立,寻求符合YashanDB技术架构落地的方案,从功能特性的细节角度,提炼并遵循了一系列的实现原则。
JAVA UDF方案:Oracle为了实现这一特性,直接将JVM集成到内核中;由于Oracle采用多进程架构,一旦用户编写的UDF存在异常,影响范围有限,可以重新启动进程。然而,由于YashanDB采用多线程架构,一旦用户要运行的代码出现异常,对我们来说是毁灭性的冲击。所以,我们需要设计一个沙箱进程,由该进程负责拉起JVM执行用户UDF。虽然这种架构会需要如协议交互和进程管理的额外工作,但对于实现技术路线的自主性和独立性是必要的。
PL/SQL语言的功能:这是Oracle绑定很多用户应用的锁链,为了降低用户应用迁移成本,YashanDB实现了大部分的PL/SQL语句,如声明、赋值、控制、跳转、循环、游标处理、SQL语句、动态SQL以及异常处理等。同时提供了全面的过程体对象,如存储过程、UDP、UDT、触发器等供用户使用。以UDT 自定义类型为例,YashanDB提供了RECORD、OBJECT、VARRAY、NESTED TABLE多种形态,支持方法的声明、支持将嵌套表形态。近期在某基金的核心交易处理系统中,完美地解决NESTED TABLE变量参与BULK导入的业务移植功能。随着应用场景的不断丰富和复杂化,存储过程的功能也将不断完善和优化。
DBLINK功能:YashanDB提供了从YashanDB到YashanDB,YashanDB到Oracle,Oracle到YashanDB的远端访问和事务能力,在这个功能点上,存在很多技术细节需要攻克,如异构数据库间数据类型、字符集的映射,计划和表达式如何进行远端下推,复杂SQL的拆分,远端事务管理,复杂DML语句联动等。
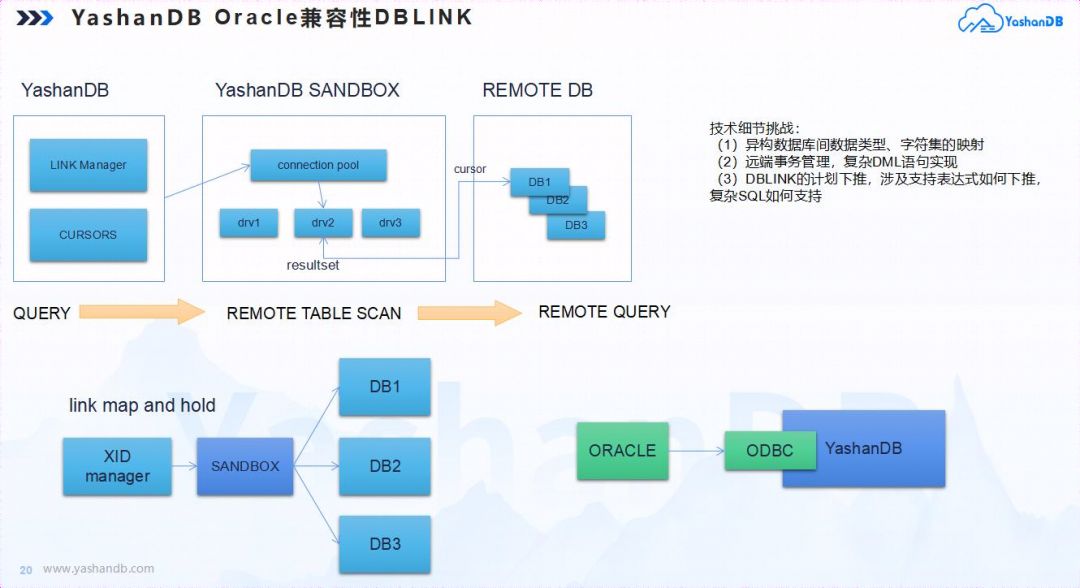 图 7 DBLINK
图 7 DBLINK - 特性对标。寻求适合我们技术架构的落地方案;
- 提炼实现原则。从功能特性角度,摸清实现细节,从细节中提炼特性的实现原则;
- 兼容不是抄袭、不能盲从。甄别Oracle的特性规格和特性实现BUG;在YashanDB开发过程不断汇总实现细节上的典型案例,同时编写开发指导文档提供用户避免踩坑;
- 预留扩展路线,为后续技术竞争力落地做好铺垫。
