网站建设实训结论与分析总结搞一个网站多少钱
目录
一,堆
堆的概念
向下调整法(数组)
向上调整法(数组)
堆的创建(建堆)
堆的实现
一,堆
堆的概念
- 如有个关键码的集合K={
,
,
,...,
},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足
<=
且
<=
(
>=
且
>=
),i=0、1、...,则称为小堆(大堆);
小堆
<=
且
<=
,即所有节点小于等于孩子;
- 根节点最小,叫做最小堆或小根堆;
大堆
>=
且
>=
,即所有节点大于等于孩子;
- 根节点最大,叫做最大堆或大根堆;
堆的性质
- 堆中某个节点的值,总是不大于或不小于其父节点的值;
- 根一定是最值(最大值或最小值);
- 堆总是一颗完全二叉树,适合顺序结构存储;
向下调整法(数组)
- 将数组看做为一颗完全二叉树,可使用向下调整法创建堆;
- 前提条件为,此二叉树的左右子树需是一个堆,只有根节点不满足堆要求;
- 从根开始,与左右子节点中的最小值,比较并交换,依次类推,直到比父亲大或到叶子节点终止;
- 时间复杂度,O(logN);
- 注,向上调整法类似;
int array[] = {27,15,19,18,28,34,65,49,25,37};

//向下调整法,小堆
void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void AdjustDown(int* arr, int n, int parent)
{int child = 2 * parent + 1;//无孩子节点或父亲小于孩子,即终止while (child < n){if (child + 1 < n && arr[child + 1] < arr[child])child++;if (arr[parent] > arr[child]){Swap(arr + parent, arr + child);parent = child;child = 2 * parent + 1;}elsebreak;}
}向上调整法(数组)
//向上调整法
void AdjustUp(int* arr, int child)
{int parent = (child - 1) / 2;//大堆//根节点或父亲大于孩子,即终止while (child > 0){if (arr[parent] < arr[child]){Swap(arr + parent, arr + child);child = parent;parent = (child - 1) / 2;}elsebreak;}
}堆的创建(建堆)
- 即对数据如数组(可看为完全二叉树),将其构建为堆;
- 方法为,从倒数第一个非叶子节点的子树开始调整,直到根节点为止;
- 即每次调整时,使用向下调整法;
- 建堆时间复杂度,O(N),下面有证明;
- 注,也可使用向上调整法建堆,但初始化堆的个别元素位置可能不一样;
int arr[] = {1,5,3,8,7,6}; //建堆-向下调整法
void Heap(int* arr, int n)
{int i = (n - 1 - 1) / 2; //最后节点的父节点for (i; i >= 0; i--){AdjustDown(arr, n, i);}
}//建堆-向上调整法
void Heap(int* arr, int n)
{int i = 1; for (i; i < n; i++){AdjustUp(arr, i);}
}
建堆时间复杂度


堆排序
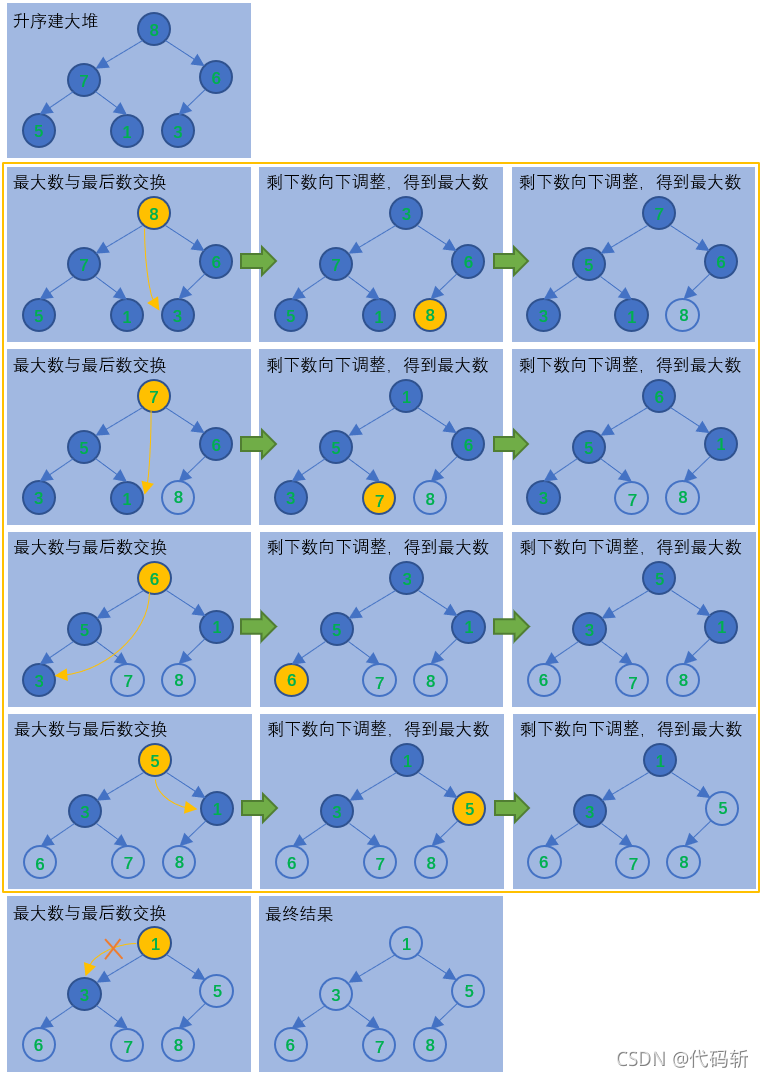
- 升序,建大堆(将最大的数换到最后,在将剩下的数向下调整下,选出次大数,依次类推);
- 降序,建小堆(将最小的数换到最后,在将剩下的数向下调整下,选出次小数,依次类推);
- 整体的时间复杂度,O(N*logN);
- 如升序建小堆(或降序建大堆)的话,选出最值后,需在继续建堆(O(N)),效率较低,还不如直接遍历,建堆的价值未体现;
//建堆排序
void HeapSort(int* arr, int n)
{//建堆 - O(N)int i = (n - 1 - 1) / 2; //最后节点的父节点for (i; i >= 0; i--){AdjustDown(arr, n, i);}//排序 - O(N*log(N))int end = n - 1;while (end){Swap(arr, arr + end);AdjustDown(arr, end, 0);end--;}
}
堆的实现
//堆
typedef int HPDataType;typedef struct Heap
{HPDataType* data;int size;int capacity;
}Heap;//初始化
void HeapInit(Heap* php, HPDataType* arr, int n);//释放销毁
void HeapDestroy(Heap* php);//插入数据并保持堆
void HeapPush(Heap* php, HPDataType* x);//删除堆顶数据并保持堆
void HeapPop(Heap* php);//返回堆顶数据
HPDataType HeapTOP(Heap* php);//返回堆节点个数
int HeapSize(Heap* php);//判断释放为空
bool HeapEmpty(Heap* php);
注:完整接口实现代码路径https://gitee.com/napoleoncode/start-code/tree/master/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/06_Heap
TOP-K问题
- 直接排序,O(N*log(N));
- 建个N个数的堆,并取出前K个数,O(N+K*log(N));
- 建个K个数的小堆,然后将剩下的数依次与堆顶比较,大即入堆,最后此堆即为最大的K个数,O(N*log(K));(如N非常大内存不够,前两种方法即适用了);
- 注,通常K远小于N;
//TOP-K
void TOPK(int* arr, int n, int k)
{Heap hp;//建堆HeapInit(&hp, arr, k);int i = k;for (i; i < n; i++){//替换if (HeapTop(&hp) > arr[i]){HeapPop(&hp);HeapPush(&hp, arr[i]);}}HeapPrint(&hp);HeapDestroy(&hp);
}